�@�@�@�@�@�@�@�@�@�@�@�ߘa�V�N�Q���R��
���告�o�̔b�큄
�b��̃��[��
�告�o�Ő�H�y�ɂR�l�̗͎m�`�C�a�C�b�������g�b�v�ŕ��ꍇ,�D��������b��ōs���B
���������ōŏ��̑ΐ�҂��`�A�a�Ƃ��A�T���̐l���b�Ƃ��܂��B
���[���͍ŏ��ɂ`�Ƃa���ΐ킵�A���̏��҂ƍT���͎m�b���ΐ킷��B
���̂��̏��҂ƍT���͎m���ΐ킷��B
�������čŏ��ɂQ�A�������͎m��D���Ƃ���B
�R�l�̗͎m���݊p�̂Ƃ�,���̂悤�ȃ��[���ŗD�������܂�܂ŁA�����̏ꍇ���l������B
�R�l�̗͎m�`�C�a�C�b���D������m���͎��`�}��p���čl���Ă݂�B
�@���`�}�ł�,�`�Ƃa�̑ΐ���Z,�a�Ƃb�̑ΐ����,�b�Ƃ`�̑ΐ�����ŕ\���B
�܂�,���ꂼ��`,�a,�b���Q�A�����ėD�������肵���ꍇ��
![]() �ƕ\���B���L�̎��`�}���,�m���������܂��B
�ƕ\���B���L�̎��`�}���,�m���������܂��B
�R�l�̎��͂��݊p�Ƃ����̂�,�e�l���e�ΐ�ŏ��m���͂P/�Q�ł��B
�@
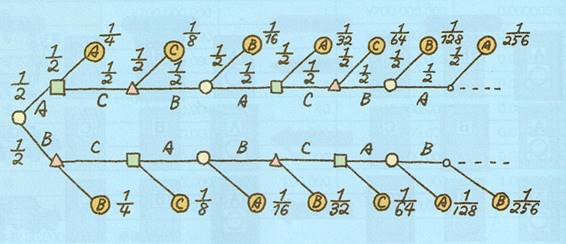
�ŏ���,�`,�a������Ă`�����m����![]() �B
�B
�ŏ��̎��g�݂���l���Ă݂��,�`�a���`�b�ł`���D������m���́A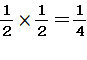 �ƂȂ�B
�ƂȂ�B
���̂悤�ɂ���,�`���D������m�����s�b�N�A�b�v���Ă݂�ƁB
�@�ŏ��̂`�Ƃa�̑ΐ�ł`���������ꍇ �E�E�E�@
�E�E�E�@
�ŏ��̂`�Ƃa�̑ΐ�ła���������ꍇ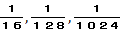 �E�E�E�A�@�ł��B
�E�E�E�A�@�ł��B
�@
������,�`�̊m�������䐔��̘a�̌�����p���ċ��߂Ă݂�B
�@�̂Ƃ��͏�����![]() ,���䂪
,���䂪![]() ���
���
�@ �@
�@![]()
�A�̂Ƃ��͏�����![]() ,���䂪
,���䂪![]() ���
���

�����,�`�̗D������m�����@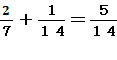 �@�ƂȂ�B
�@�ƂȂ�B
�܂��A���`�}����a�̗D������m���������ł��B
�����ɁA�b�̗D������m����
�@�ȏォ��A�`,�a,�b�̗D������m���̔��,�`�F�a�F�b���T�F�T�F�S
�m���͂`���a��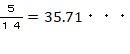 �C�b��
�C�b��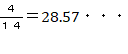 ���̂悤�Ȕb��͍ŏ��ɂQ������܂ʼni���ɑ����܂��B
���̂悤�Ȕb��͍ŏ��ɂQ������܂ʼni���ɑ����܂��B
���[���I�ɂ�,�ŏ��̍T���͎m�͖�V���̕s��������A�b��͌����ł͂���܂���B
�@�ł́A�����Ȑ킢���̓��[�O��ɂ����@�ł��B
�ŏ���,�`�Ƃa���킢�A�`�Ƃa�̔s�҂ƍT���̂b���킢,
�Ō�ɂ`�Ƃa�̏��҂Ƃb�Ɛ킢�܂��B�R�l�łQ�������͎m�̗D���ł��B
�Ƃ��낪,�R�l��1���P�s�̂Ƃ���,�ēx,�R�l�̂�郊�[�O��̍ĊJ�ł��B
�N�����Q������܂ŁA���̃��[�O����J��Ԃ��܂��B
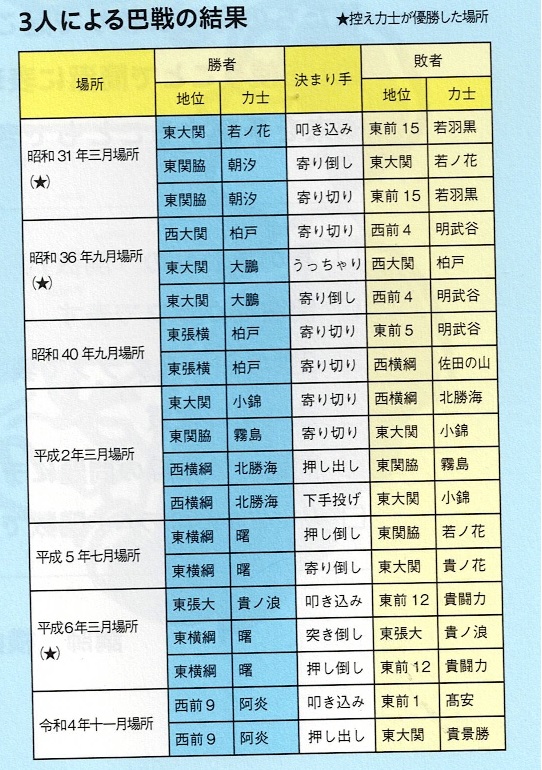
�Q�l�ɁA�ߋ��̂R�l�ɂ��b��̌��ʂ������Ă����܂��B
�ŋ߂ł�,�ߘa�V�N1���ꏊ�ɂ���,���L�̌���,��ց@�L�������D��
�����@����R���@����@�Z��ց@�L����
�����@���Q�@���@���|���@�Z��ց@�L����
 �Q�l�����@�m�g�j�e�L�X�g�@�R�����Ń}�X�^�[���鐔�w�@2024�N7���`9���@
�Q�l�����@�m�g�j�e�L�X�g�@�R�����Ń}�X�^�[���鐔�w�@2024�N7���`9���@