平成15年1月15日
 [流れ星]
[流れ星]
第111回数学的な応募問題解答NO2
<解答募集期間:1月1日〜1月15日>
[tanのn倍角]
* 太郎さんは、先日生徒から、「三角関数のsin3θをsinθ、
cos3θ をcosθ で表す3倍角の公式があるのに、tan3θを
tanθで表す公式はないのですか。あれば、教えてください。」という質問を受けました。そのときは、私の見たことがないから、「必要なら、自分で作ったら。」。と言っておきました。このことを、問題にします。tanθ=t とおくとき、次の設問に答えてください。
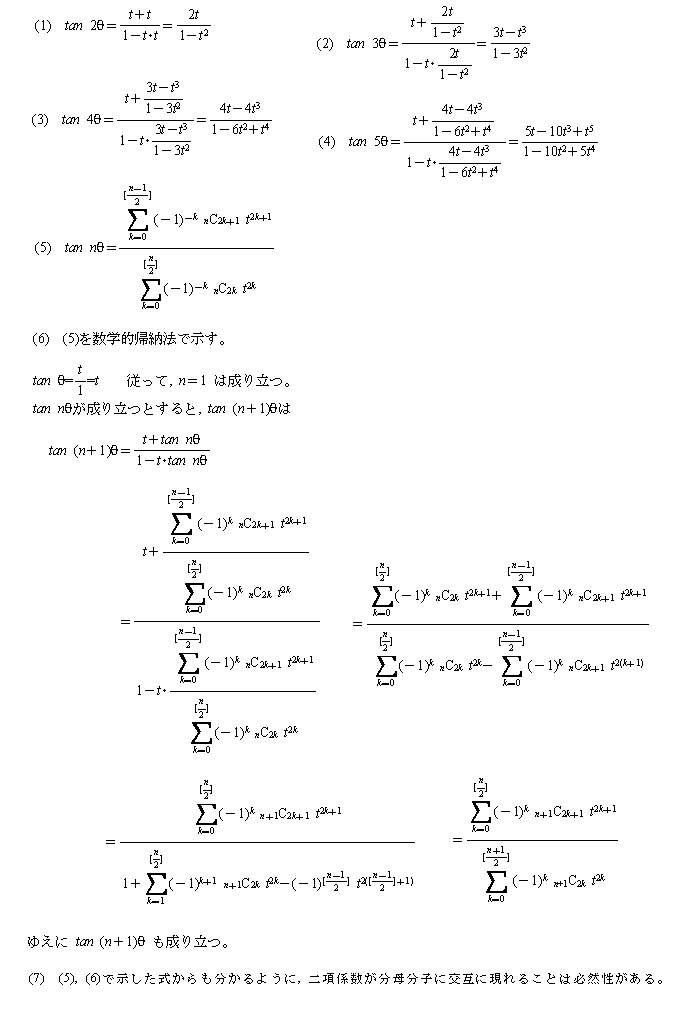
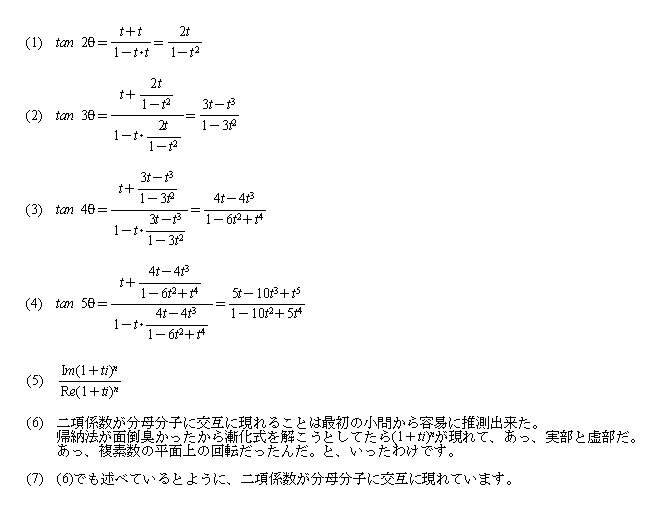
(1)tan2θをtで表せ。(これは公式ですから、結果だけでいいです。)
(2)tan3θをtで表せ。
(3)tan4θをtで表せ。
(4)tan5θをtで表せ。
(5)今までの答えから、類推して、tannθをnとtで表せ。
(6)(5)の予想が正しいことを数学的帰納法で示してください。
追加(7)実はこの計算をしていたら、分母、分子の係数が有名な数列になっていることに気がつきました。必然性があるのでしょうか。
疑問に思っています。どなたか 教えてください。
NO7「中川幸一」さん 1/14: 03時26分 受信 更新1/16 NO8「佐藤 栄介」さん 1/14 :
04時11分 受信 更新1/16 <水の流れ:コメント>全員の方が、解答を作成するのに、多くの時間をかけておられて、大変恐縮しています。 受験生に、tanのn倍角の公式も作れば出てくることを知ってもらいたいです。
「H7K」さんには、画像をgifで送信くださいまして感謝しています。
また、nが奇数、偶数をガウス記号[ ]で「H7K」さんと「三角定規」さんはうまく表現してありました。
さらに、n+1Ck=nCk+nCk-1を利用して 数学的帰納法で証明されていましたし、「Toru」さんは、複素数を用いての解答は数学って本当に自由性があるんだなーと実感させられました。
tan nθ=((cosθ+isinθ)^n-(cosθ-isinθ)^n)/((cosθ+isinθ)^n+(cosθ-isinθ)^n)i
=((1+it)^n-(1-it)^n)/((1+it)^n+(1-it)^n)i はどこかで利用できないかなと思います。
「Kashiwagi」さん「浜田」さんの解答には、表現方法に苦労の後が感ぜられます。
「udonko」さん「中川幸一」さんは、初めての参加でしたが、これからもよろしくお願いします。
「佐藤 栄介」さんが、複素平面の回転を利用そいた解法には、驚嘆しています。![]()
