
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂暯惉侾侾擭係寧侾俀擔
丂丂丂

 丂丂丂丂丂丂
丂丂丂丂丂丂
丂丂丂丂戞侾俁夞
悢妛揑側墳曞栤戣丂亙夝摎曞廤婜娫丗係寧侾俀擔乣係寧俀係擔亜
丂丂丂丂
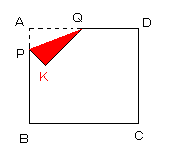
乵愜傝嬋偘偨捀揰偺斖埻乶丂丂丂偙偙偵丄侾曈偑俀們倣偺惓曽宍偺愜傝巻俙俛俠俢偑偁傝傑偡丅
丂丂丂壓偺恾偺傛偆偵丄曈俙俛丄俙俢忋偺揰俹丄俻傪愜傝栚偲偟偰丄
丂丂丂俁妏宍俙俹俻傪愜偭偨偲偒丄捀揰俙偺棃傞埵抲傪俲偲偟傑偡丅
丂丂丂俹丄俻偑偦傟偧傟曈俙俛丄俙俢忋傪帺桼偵摦偔偲偒丄揰俲偺
丂丂丂摦偔斖埻偺柺愊傪媮傔側偝偄丅
丂丂丂懢榊偝傫傕摱怱偵偐偊偭偰丄偄傠偄傠偲愜傝嬋偘偰峫偊傞偙偲偵偟傑偟偨丅
丂丂丂丂奆偝傫傕丄峫偊偰偔偩偝偄丅丂
丂
丂亙嶲峫暥專丗僷僘儖傛傝柺敀偄拞妛擖帋偺嶼悢乯島択幮亜丂
丂丂儊乕儖偱憲偭偰偔偩偝偄丅懸偭偰偄傑偡丅
丂丂<帺戭亜丂丂
mizuryu@aqua.ocn.ne.jp丂
丂亙俙倱倎倣倝亜丂偝傫偺夝摎係寧侾俁擔丂俻傪俢偵偰屌掕偟偰俹傪摦偐偡偲丄俲偼俢傪拞怱,敿宎俢俲,
拞怱妏90搙偺愵宍偺屖傪昤偒傑偡丅乧乧嘆
媡偵俹傪俛偵偰屌掕偟偨偲偒俲偼俛傪拞怱,敿宎俛俲,
拞怱妏90搙偺愵宍偺屖傪昤偒傑偡丅乧乧嘇
俻傪擟堄偵(俙俢忋偱)屌掕偟偰俹傪摦偐偟偨偲偒俲偼俙偐傜僗僞乕僩
偟偰敿宎俻俲偺墌廃(偺堦晹)傪昤偒傑偡偑丄(俹偑俛偵棃偨偲偒偼
敿宎俛俲偲傒側偣傞偺偱)嘇偺廃忋偱僗僩僢僾偟傑偡丅乧乧嘊
屌掕揰俻傪俢偐傜俙傊楢懕揑偵摦偐偡偲丄嘊偺傛偆側墌屖偼楢懕揑偵
弅傑偭偰峴偔偺偱丄寢嬊嘆,嘇偵傛偭偰埻傑傟偨恾宍偺撪晹傪偔傑側偔
摦偔偙偲偵側傝傑偡丅廬偭偰丄柺愊偼俀兾亅係偲側傝傑偡丅
嶲峫偵恾傪尒偰偔偩偝偄
丂
戞侾俁夞悢妛揑側墳曞栤戣夝摎
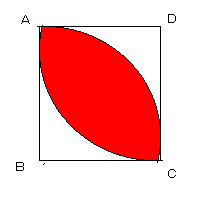
丂廫恑俛俙俽俬俠偺僾儘僌儔儉傪嶌惉偟媮傔傑偟偨丏撪梕偼師偺捠傝偱偡丏
丂傑偢俙(亅侾,侾)丆俛(亅侾,亅侾)丆俠(侾,亅侾)丆俢(侾,侾)丆俹(亅侾,侾亅俙俹)丆俻(亅侾亄俙俻,侾)丆俲(倃,倄)偲
嵗昗傪摫擖偟傑偡丏偡傞偲俲偼捈慄俹俻偵懳偟偰丆俙偲懳徧偱偡丏
丂俙俲佦俹俻偐傜丆(倄亅侾)乛(倃亄侾)丒俙俹乛俙俻亖亅侾
丂丂亪俙俻丒倃亄俙俹丒倄亖俙俹亅俙俻乧乧嘆
丂捈慄俹俻偺曽掱幃偼丆倷亅侾亖俙俹乛俙俻丒{倶亅(亅侾亄俙俻)}
丂俙俲偺拞揰((倃亅侾)乛俀,(倄亄侾)乛俀)傪捠傞偺偱丆
丂丂俙俹丒倃亅俙俻丒倄亖俀丒俙俹丒俙俻亅俙俹亅俙俻乧乧嘇
丂嘆丆嘇傪倃丆倄偺楢棫曽掱幃偲偟偰夝偒丆揰傪僾儘僢僩偟偰丆偙偺恾宍傪媮傔傟偽傛偄丏
丂偡傞偲恾宍偼丆惓曽宍撪晹偵偁傝丆俛丆俢傪拞怱偲偟丆敿宎俀偺墌廃偵傛偭偰埻傑傟偨傕偺偲暘偐傝傑偡
乮恾嶲徠乯丏

丂偟偨偑偭偰媮傔傞柺愊偼丆
丂丂(兾丒俀^2乛係亅俀^2乛俀)丒俀亖俀兾亅係乮暯曽僙儞僠乯
偱偡丏
丂杮摉偼丆柺愊傕帺摦揑偵媮傔傜傟傞僾儘僌儔儉偵偟偨偐偭偨偺偱偡偑丆帪娫偺娭學偱柍棟偱偟偨丏巆擮偱偡丏
丂偺傫傃傝偟偰偄偨傜丆婜尷傪夁偓偰偟傑偭偨傛偆偱偡丏怽偟栿偁傝傑偣傫偱偟偨丏
丂丂丂丂丂丂丂丂丂丂丂丂丂
!ORIMAGE.10B
SET WINDOW -2,2,-2,2
LET KIZAMI=.01
LET TEN_HANKEI=.01
SET LINE COLOR "BLACK"
PLOT LINES:-1,1;-1,-1;
PLOT LINES:1,-1;1,1;
PLOT LINES:-1,1
SET LINE COLOR "RED"
FOR AQ=0+KIZAMI TO 2-KIZAMI STEP KIZAMI
FOR AP=0+KIZAMI TO 2-KIZAMI STEP KIZAMI
LET A=AQ
LET B=AP
LET C=AP
LET D=-AQ
LET P=AP-AQ
LET Q=2*AP*AQ-AP-AQ
LET BUMBO=A*D-B*C
LET X=(D*P-B*Q)/BUMBO
LET Y=(A*Q-C*P)/BUMBO
FOR T=0 TO 2*PI STEP PI/9
PLOT LINES:X+TEN_HANKEI*COS(T),Y+TEN_HANKEI*SIN(T);
NEXT T
NEXT AP
NEXT AQ
END
丂丂丂
丂丂丂丂丂丂丂丂丂
丂丂丂丂<帺戭亜丂丂
mizuryu@aqua.ocn.ne.jp丂
丂
![]()
 丂
丂