
平成11年5月5日
 [流れ星]
[流れ星]
第15回
数学的な応募問題<解答募集期間:5月5日〜5月22日>
<解答募集延長期間:〜5月29日>
[ダーツの確率]

太郎さんのお子さんは中学生です。次のような問題をもらって来ました。
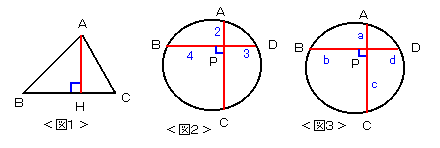
このとき、三角形ABCの外接円の半径を、2辺の長さAB,ACと
垂線の長さAHで表しなさい。(図1参照)
BDがあります。このとき、AP=2,BP=4,CP=3でした。
この円の半径を求めなさい。(図2参照)
BDがあります。このとき、AP=a,BP=b,CP=c,DP=d
でした。この円の半径を a,b,c,dを用いて表しなさい。
(図3参照)
太郎さんは、先日のゴールデンウイークにある電気店の大売り出しに
行って来ました。ここで、問題です。
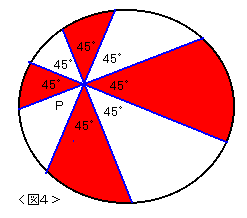
競技を行っていました。的内の任意の点Pで交わる4本の弦を引き、
的を8つの部分に分けてありました。
ただし、4本の弦はそれぞれ45度で交わっていました。
この8つの部分を交互に赤と白に4つに塗り分けてありました。
赤が当たりで、白がはずれです。当たりである確率求めてください。
はずれの確率が気になってしかたがありません。
皆さんも、考えてください。
<浜田 明巳>さんからの解答5月12日
第15回数学的な応募問題(ダーツの確率)解答
問題4を十進BASICのプログラム
mondai15.10bを作成し求めました.内容は次の通りです.的を原点中心,半径1の円とします.乱数を使って,4本の弦の交点
(xc,yc)を求め,x軸とのなす角をt+π/4*j(j=1,2,3,4,0≦t<π/2)とします.4直線の方程式は,f(j)=(x-xc)*sin(t+π/4*j)-(y-yc)*cos(t+π/4*j))=0
となります.
ダーツが当たった場所を
(x,y)とし,f(1)*f(2)*f(3)*f(4)の符号が正のとき当たり,負のときはずれとします.当たりを赤の点,はずれを黒の点で表示します.この試行を1000000(
max)回繰り返し,確率を求めます.このプログラムにより,答は,
499652 / 1000000 = .499652
つまり,1/2となります.
浜田 明巳
!mondai15.10b
set window -1.1,1.1,-1.1,1.1
randomize
dim lx(4,2),ly(4,2)
let max=1000000
let count=0
let xc=1
let yc=1
do while sqr(xc*xc+yc*yc)>1
let xc=2*rnd-1
let yc=2*rnd-1
loop
let t=pi*.5*rnd
for j=0 to 3
if cos(t+pi*.25*j)<>0 then
let a=1+tan(t+pi*.25*j)*tan(t+pi*.25*j)
let b=2*(yc-xc*tan(t+pi*.25*j))*tan(t+pi*.25*j)
let c=(yc-xc*tan(t+pi*.25*j))*(yc-xc*tan(t+pi*.25*j))-1
let d=b*b-4*a*c
for jj=1 to 2
let lx(j+1,jj)=(-b+(3-2*jj)*sqr(d))*.5/a
let ly(j+1,jj)=(lx(j+1,jj)-xc)*tan(t+pi*.25*j)+yc
next jj
else
for jj=1 to 2
let lx(j+1,jj)=xc
let ly(j+1,jj)=(3-2*jj)*sqr(1-xc*xc)
next jj
end if
next j
set line color "green"
for tt=0 to 2*pi step pi/360
plot lines:cos(tt),sin(tt);
next tt
plot lines
for j=1 to 4
plot lines:lx(j,1),ly(j,1);lx(j,2),ly(j,2)
next j
for kaisuu=1 to max
let x=1
let y=1
do while sqr(x*x+y*y)>1
let x=2*rnd-1
let y=2*rnd-1
loop
let fugou=1
for j=0 to 3
let fugou=fugou*sgn((x-xc)*sin(t+pi*.25*j)-(y-yc)*cos(t+pi*.25*j))
next j
if fugou>=0 then
let count=count+1
set line color "red"
else
set line color "black"
end if
plot lines:x,y
next kaisuu
print count;"/";max;"=";count/max
end
P>

浜田さんから、4番についてパソコンを利用した解法を頂きましたが、他の解法も考えられます。
是非、1,2,3番を利用した解答をお待ちしています。
<ヨッシー>さんからの解答5月20日
1.答え:AB・AC/2AH
考え方:
実際に外接円を書き、AHの延長と外接円との交点をDとします。
BCの中点をMとします。
BCの垂直二等分線と、ADの垂直二等分線の交点Nが外接円の中心、
NCが半径となります。
三角形MNCについて、∠NMC=90度より
NC^2=MC^2+MN^2
MC=BC/2,MN=|(AH−HD)/2|
BC=BH+HC=√(AB^2−AH^2)+√(AC^2−AH^2)
HD=BH・CH/AH △AHC∽△BHDより。
を代入して整理すると、求められます。
2.答え:√65/2
考え方:
△ABDに、問題1の結果を当てはめると、
AB=2√5、AD=√13、AP=2
より、半径=AB・AD/2AP=√65/2
3.答え:√(a^2+b^2+c^2+d^2)/2 (√は分子だけ)
考え方:
問題1と同じ考え方で、BDの中点をM、外接円の中心をNとすると、
三角形MNDについて、∠NMD=90度より
ND^2=MD^2+MN^2
={(b+d)/2}^2+{(a-c)/2}^2
ここで、△APD∽△BPC より、 ac=bd を考慮すると、
答えのようになります。
<水の流れ:コメント>5月20日
1番の問題は、他にもいろいろな解法があります。
2番、3番はそれを利用して、解くことができます。
当初、4番だけを作って、出題する予定でしたが、難しいと思って、誘導式にしてあります。
4番の解答をお待ちしています。
皆さん、答えがわかったら、その答えになる考え方とペンネームを添えて、
メールで送ってください。待っています。
![]()
![]()