
平成11年5月24日


第16回
数学的な応募問題<解答募集期間:5月24日〜6月5日>
[ダーツの期待値]
太郎さんは、先日のゴールデンウイークに、岐阜県大垣市長松にある
電気店パナシーズンの大売り出しに行って来ました。ここで、問題です。
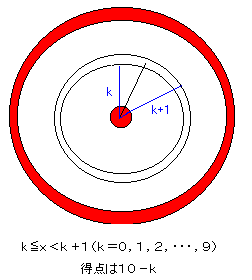
中心がOで、半径10の円板が的でして、同心円上に、半径9,8,7,…、2,1
の円が書いてありました。得点は小さい円環(一番小さいのは円)から順に、10点、
9点、8点、…、最後は1点でした。この得点分だけ、参加者に賞品がもらえます。
円板内の点をまったくでたらめに1回選んだときの得点の期待値を求めてください。
太郎さんは童心にかえって、ダーツ競技を楽しんでいましたが、この電気店にとって、
賞品の数をどれだけ用意しておいたか、気になってしかたがありません。
皆さんも、考えてください。
メールで送ってください。待っています。
<YokoyaMac>さんからの解答5月24日受信
answer : 3.85
解法 :
%%%texで書きます.%%%
\begin{document}
k点獲得する確率は,
\[
\frac{(11-k)^2\pi -(10-k)^2\pi }{10^2\pi} = \frac{2k+1}{100}
\]
であるから,求める期待値は,
\[
\sum_{k=1}^{10}k\times \frac{2k+1}{100} = \frac{385}{100} = 3.85
\]
\end{document}
%%%以上です.%%%
<数楽者>さんからの解答5月25日受信
第16回数学的な応募問題
解答 3.85点
解法 一番小さい円の面積を1とする。
最高点を n とする。
得点が n−k+1 である確率は (2k−1)/n^2 である。
(k=1,2,・・・,n)
得点と確率の積和をとれば、得点の期待値が
(n+1)(2n+1)/6n
と求まる。n=10 を代入すれば、3.85になる。
<浜田 明巳>さんからの解答6月1日受信
QBASICのプログラムoubo.qbを作成し求めました.内容は次の通りです.
的を原点中心,半径10の円とします.乱数を使って円内の点(x,y)を求め,原点からの距離dを計算します.0≦d≦1のとき10点,1<d≦2のとき9点,2<d≦3のとき8点,………,9<d≦10のとき1点とします.この試行を1000000(max)回繰り返し,期待値を求めます.
このプログラムにより,答は,
3847429/1000000=0.3847429
つまり,0.385となります.
これは半径n(nは自然数)のときの期待値
Σ(k=1〜n){n−(k−1)}{πk^2−π(k−1)^2}/(πn^2)
=(n+1)(2n+1)/(6n)(=Σ(k=1〜n)k^2/n^2)
にn=10を代入した結果の0.385と一致します.
ちなみに,各点の出た回数は次の通りです.
1点 189760回
2点 170482回
3点 150907回
4点 129494回
5点 109687回
6点 89991回
7点 69753回
8点 49890回
9点 30124回
10点 9912回
計算時間は,私のノートパソコンで7時間かかりました.
浜田 明巳
'oubo.qb
SCREEN 12: CLS : RANDOMIZE TIMER
yoko = 640: tate = 400: xcenter = yoko * .5: ycenter = tate * .5: hankei = 10
kakudai = tate / (hankei * 2) * .8: iro0 = 7
max = 1000000!: kaisuu = 0: goukei = 0
DIM ten(hankei): FOR j = 1 TO hankei: ten(j) = 0: NEXT
DEF fnx (x) = xcenter + kakudai * x: DEF fny (y) = ycenter - kakudai * y
FOR j = 1 TO hankei: CIRCLE (fnx(0), fny(0)), kakudai * j, iro0: NEXT
WHILE kaisuu < max AND INKEY$ = "": kaisuu = kaisuu + 1
DO
x = (RND * 2 - 1) * hankei: y = (RND * 2 - 1) * hankei
d = SQR(x * x + y * y)
LOOP WHILE d > hankei
IF d = 0 THEN ten = 10 ELSE ten = 11 + INT(-d)
goukei = goukei + ten: ten(ten) = ten(ten) + 1
PSET (fnx(x), fny(y)), ten
LOCATE 1, 1: PRINT USING "###ten"; ten
PRINT USING "########/#######=###.######"; goukei; kaisuu; goukei / kaisuu
FOR j = 1 TO hankei: COLOR j: PRINT USING "###ten:#######kai"; j; ten(j)
NEXT: COLOR iro0
WEND: WHILE INKEY$ <> "": WEND: END
PS.添付ファイルはVISUAL BASICで作っており,よけいなことをはぶき,
100000回の施行で終わりますので,1,2分で終わるはずです.
<コメント:水の流れ> VISUAL BASICをホームページに載せる技量をまだ、
身についていませんので、しばらく、お待ちください。
<自宅> mizuryu@aqua.ocn.ne.jp
![]()
![]()