
平成12年1月30日


第44回
数学的な応募問題<解答募集期間:1月30日〜2月13日>
[正2n角形]
1月31日に、「sambaGREEN」さんから、『「正n角形」となっていますが,例をみると,「正2n角形ですね」正2n角形として,解答します。』とご指摘がありましたので、修正しました。
太郎さんは、円に内接している正2n角形を描いています。この図形の頂点をn組のペアに分ける方法の中で、
それぞれのペアを結ぶn本の線分が互いに交わらないように分ける方法を考えてみました。
この分け方の方法をf
(n)としたとき、次の問題に答えてください。ただし、f
(0)=1, f(1)=1と便宜上します。また、n=2ときは参考に図に書いておきます。ここから、f
(2)=2になっています。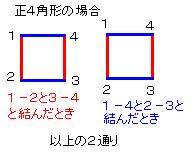
問題1:n=3,4のとき、f
(n)を求めてください。問題2:f
(n)の漸化式を作って、一般項f(n)をnで表してください。太郎さんは、早速、正6角形や。正8角形を描いて考えてみようと思っています。
皆さん、答えがわかったら、その答えになる考え方とペンネームを添えて、
メールで送ってください。待っています。
<自宅>
mizuryu@aqua.ocn.ne.jp![]()
