平成１２年７月１６日

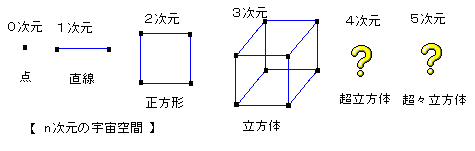
［ｎ次元宇宙空間］

　太郎さんは、ときどき　夜空を見上げて、果てしなく続く宇宙空間を眺めています。

このとき、０次元の世界に住んでいると、そこには点の世界だから、境界はひとつ「頂点」があるだけです。

この点を動かしてみると、１次元の世界ができあがるが、ここには「線」でしかない。これには、「境い目」が２つある。

その両端である。言いかえれば、「２つの０次元境界（頂点）と１つの１次元境界（線）とがある」と言える。

　さて、この直線を横にその長さだけ引っ張ると、正方形ができる。すると、頂点の数は、以前あった２から４に倍増している。

また、正方形では４つの直線、つまり辺が４本あり、さらに、１枚の２次元境界（面）がここではじめて出てくる。

　さて次ぎに、２次元の平面から上に向かって離れていくと、例えば、正方形を上にうまく移動すれば、立方体を作ることができ

る。４つの頂点の動いた軌跡がまず４本の線を作りだすから、辺は１２本、頂点は８個、面は２次元では、１枚しかなかったが、

一挙６枚になっている。

これを、繰り返して、４次元の超立方体、５次元の超々立方体、・・・。ｎ次元の超々々・・・立方体を考えていきます。

ここには、ｎ次元空間の世界があるのです。

このときの０次元境界（頂点）、１次元境界（辺）、２次元境界（面）、３次元境界（立体）、・・・、（ｎ―１）次元境界

（名前はまだできていない）の数を調べたいのです。ここには、オイラーの多面体定理が成り立つと思っていますが、・・・・

何せ、頭の中でしか想像できない超々々・・・立方体ですので、困っています。

ここで、問題です。

問題１：４次元の「超立方体」には境界になる、点、辺、面、立体がそれぞれいくつあるでしょう。

問題２：一般に、ｎ次元の「超々々・・・立方体」には境界になる、点、辺、面、立体、・・・、（ｎ―１）次元境界の数は

一体いくつあるでしょう。一般式が求められています。皆さん考えてください。

＜ヒント：群数列でみると、（１）、（１，２）、（１，４，４）、（１，６，１２，８）、・・・・＞

　解けた問題だけでも良いから、皆さん、答えがわかったら、その答えになる考え方とペンネームを添えて、

　　メールで送ってください。待っています。