平成13年9月1日
 [流れ星]
[流れ星]
第82回数学的な応募問題
<解答募集期間:9月1日〜9月15日>
[三角形の面積比]
太郎さんは、最近「ヴェイユ」さん頂いた「面積比」の問題を考えていたときに、下のような問題を気がつきました。
鋭角三角形ABCにおいて、内部に任意に点Pをとり、直線APと辺BCとの交点をD,直線BPと辺CAとの交点をE,直線CPと辺CAとの交点をFとする。また、「チェバ」の定理から、BF:FA=p:q,AE:EC=r:p,CD:DB=q:rとおける。(ただし、p,q,rは正の数で、便宜的にp+q+r=1とする。)
このとき、問題1:面積比、三角形DEF/三角形ABCの値をp,q,rで簡単に表してください。
さらに、ここで、BC=a,CA=b,AB=cとし、点Pが次のような場合、p:q:rの比を辺a,b,cや角A,B,Cなどを用いて求めてください。(ただし今回は、p+q+r=1の制約を取り除きます。)
問題2:点Pが重心の場合
問題3:点Pが内心の場合
問題4:点Pが外心の場合
問題5:点Pが垂心の場合
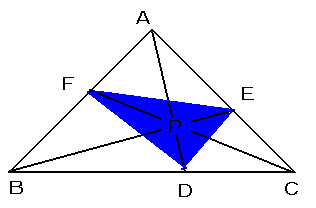
でも、点Pが問題2,3,4、5のときの面積比、三角形DEF/三角形ABCの値がどうなるか気になります。わかったら教えてください。
皆さん、考え方がわかったら、全部でなくていいですから、とペンネームを添えて、メールで送ってください。待っています。
![]()
