平成13年9月15日
 [流れ星]
[流れ星]
第82回数学的な応募問題解答
<解答募集期間:9月1日〜9月15日>
[三角形の面積比]
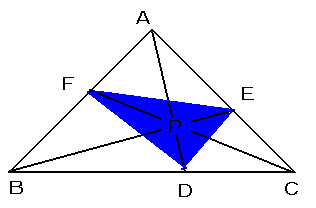
太郎さんは、最近「ヴェイユ」さん頂いた「面積比」の問題を考えていたときに、下のような問題を気がつきました。
鋭角三角形ABCにおいて、内部に任意に点Pをとり、直線APと辺BCとの交点をD,直線BPと辺CAとの交点をE,直線CPと辺CAとの交点をFとする。また、「チェバ」の定理から、BF:FA=p:q,AE:EC=r:p,CD:DB=q:rとおける。(ただし、p,q,rは正の数で、便宜的にp+q+r=1とする。)
このとき、問題1:面積比、三角形DEF/三角形ABCの値をp,q,rで簡単に表してください。
さらに、ここで、BC=a,CA=b,AB=cとし、点Pが次のような場合、p:q:rの比を辺a,b,cや角A,B,Cなどを用いて求めてください。(ただし今回は、p+q+r=1の制約を取り除きます。)
問題2:点Pが重心の場合
問題3:点Pが内心の場合
問題4:点Pが外心の場合
問題5:点Pが垂心の場合
でも、点Pが問題2,3,4、5のときの面積比、三角形DEF/三角形ABCの値がどうなるか気になります。わかったら教えてください。
NO1:「浜田」さんの解答 9/3:8時14分受信 9/15更新
問題1
△AFE/△ABC=q/(p+q)・r/(r+p)=qr/(p+q)(r+p)
同様に,
△BDF/△ABC=rp/(q+r)(p+q)
△CED/△ABC=pq/(r+p)(q+r)
∴△DEF/△ABC=(△ABC−△AFE−△BDF−△CED)/△ABC
=1−△AFE/△ABC−△BDF/△ABC−△CED/△ABC
=1−qr/(p+q)(r+p)−rp/(q+r)(p+q)−pq/(r+p)(q+r)
={(p+q)(q+r)(r+p)−qr(q+r)−rp(r+p)−pq(p+q)}/(p+q)(q+r)(r+p)
=(pqr+p^2q+pr^2+p^2r+q^2r+pq^2+qr^2+pqr−q^2r−qr^2−r^2p−rp^2−p^2q−pq^2)/(p+q)(q+r)(r+p)
=2pqr/(p+q)(q+r)(r+p)………(答)
(疑問点)p+q+r=1は必要ない条件だと思います.p>0,q>0,r>0だけで十分ではないでしょうか.
<水の流れ:コメント>こんにちは。いつもお世話になっています。今回の応募ありがとうございます。いつも感謝の気持ちで一杯です。
「私の一日」に載せておきましたが、当初、位置ベクトルで考えていまして、
ご指摘のように 条件 p+q+r=1はなくしてもいいです。ご指摘、ありがとうございます。
問題2
点Pが重心なので,D,E,FはそれぞれBC,CA,ABの中点である.
p=q=r=1としてよいので,答は, 2/(2・2・2)=1/4
問題3
点Pが内心なので,ADは∠BACの二等分線である.
∴BD:DC=AB:AC
∴r:q=(p+q):(r+p)
∴r(r+p)=q(p+q)
∴r^2+rp=pq+q^2
∴r^2−q^2=pq−rp
∴(r+q)(r−q)=p(q−r)
∴(p+q+r)(r−q)=0
p+q+r>0から,q=r
同様に,r=p,p=r
∴p=q=r
問題2と同様なので,答は1/4
<水の流れ:コメント> ∴r:q=(p+q):(r+p) ここは、疑問です。成り立たないと思いますが。
NO2「kashiwagit」さんの解答 9/10:8時04分受信 9/15更新
おはようございます。解答を送付致します。全て面積比で考えて見ました。但し、あまりきれいな関係にならず、自信はありません。
問題1
△AEF/△ABC=(q/p+q)×(r/p+r)、他の△BDF、△CDEも同様にして
△BDF/△ABC=(p/p+q)×(r/q+r)
△CDE/△ABC=(q/r+q)×(p/p+r)となる。
△DEFの面積は△ABCから△AEF、△BDF及び△CDEの面積をひいたものだから
〔△ABC−(△AEF+△BDF+△CDE)〕/△ABCを考える。
上記3式とp+q+r=1の関係を使い整理すると、
△DEF/△ABC=1−〔2pqr/(1−p)(1−q)(1−r)〕となる。
問題2
Pが重心 : 例えば△ABDと△ADCの面積は等しいので
(r/q+r)acsinB = (q/q+r)absinC、同様にして、
(q/p+q)bcsinA = (p/p+q)casinB
この関係より p:q:r=bcsinA :acsinB :absinC
問題3 Pが内心
内心だから各々の角は二等分されている。因って、BD:DC=AB:AC同様の関係から
r/q=c/b,p/r=a/c,q/p=b/a
これらより、p:q:r=a :b :c
問題4 Pが外心
小さな三つの三角形の面積比を計算する。
例えば、△PBCは(1/2)acsinBp/p+q+r、同様にして、他の二つを求め、比較すると、
p:q:r=sin2A:sin2B:sin2C
問題5 Pが垂心
上記と同様の計算を繰り返し、面積比より
p:q:r=a cosCcosB :b cosCcosA
:c cosBcosA
問題6 問題1と同様の考えで計算すると、2pqr/(p+q)(q+r)(r+p) となる。
<水の流れ:コメント>>問題5において、
p:q:r=a cosCcosB :b cosCcosA :c cosBcosA
現在検証中ですが、比ですから、結果の形がいろいろあります。私の予定は tanA : tanB : tanC ですけど。
NO3「kashiwagit」さんの解答 9/13:7時28分受信 9/15更新
再度考えた結果を送付致します。
おはようございます。解答を送付致します。全て面積比で考えて見ました。但し、あまりきれいな関係にならず、自信はありません。
問題1 △AEF/△ABC=(q/p+q)×(r/p+r)、他の△BDF、△CDEも同様にして
△BDF/△ABC=(p/p+q)×(r/q+r)
△CDE/△ABC=(q/r+q)×(p/p+r)となる。
△DEFの面積は△ABCから△AEF、△BDF及び△CDEの面積をひいたものだから
〔△ABC−(△AEF+△BDF+△CDE)〕/△ABCを考える。
上記3式とp+q+r=1の関係を使い整理すると、
△DEF/△ABC=1−〔2pqr/(1−p)(1−q)(1−r)〕となる。
=p(superscript: 2)/(1−q)(1−r)+q(superscript:
2)/(1−r)(1−p)+r(superscript: 2)/(1−p)(1−q)
問題2 Pが重心
例えば△ABDと△ADCの面積は等しいので
(r/q+r)acsinB = (q/q+r)absinC、同様にして、
(q/p+q)bcsinA = (p/p+q)casinB
この関係より p:q:r=bcsinA :acsinB :absinC これらは全て△ABCの面積の半分だから等しく、
=1:1:1
問題3 Pが内心
内心だから各々の角は二等分されている。因って、BD:DC=AB:AC同様の関係から
r/q=c/b,p/r=a/c,q/p=b/a
これらより、p:q:r=a :b :c
問題4 Pが外心
小さな三つの三角形の面積比を計算する。
例えば、△PBCは(1/2)acsinBp/p+q+r、同様にして、他の二つを求め、比較すると、
p:q:r=sin2A:sin2B:sin2C
問題5 Pが垂心
上記と同様の計算を繰り返し、面積比より
p:q:r=a cosCcosB :b cosCcosA
:c cosBcosA これらをcosAcosBcosC で割り正弦定理を使うと、
=tanA :tanB :tanC
問題6 問題1と同様の考えで計算すると、2pqr/(p+q)(q+r)(r+p)となる。
<水の流れ:コメント>ありがとうございました。この辺のところは生徒に話してみたいと考えています。しかし、問題6では、この形ではまだ、自分自身はっきりとしていません。もし、お時間があれば、教えてもらいたいです。
![]()
