平成14年6月1日
 [流れ星]
[流れ星]
第99回数学的な応募問題
<解答募集期間:6月1日〜6月15日>
[最長距離数]
太郎さんは、よく「図1のような碁盤の目になった町で、A地点からB地点への最短距離で行く道順の総数を求めよ。」と言う問題に出合います。これは組み合わせの考え方で解くことができます。
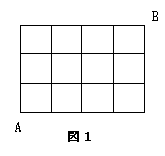
では、A地点からB地点へくねくねと遠回りをして行くと、最長距離数は幾つになるか。また、道順の総距離数は幾つになるかを考えました。ただし、同じ道を1回しか通れないものとし、小正方形の1辺の長さを1とする。
例えば、図2の1辺が2の正方形の場合は、総距離数Pは12,最短距離数Sは4、最長距離数Lは8になります。
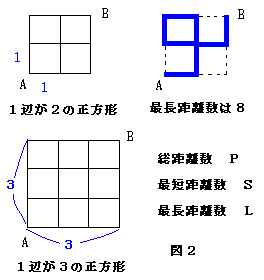
ここで、問題です。
問1.1辺が3の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問2.1辺が4の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問3.1辺が5の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問4.1辺がnの正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
次に、長方形の碁盤の目を考え、1辺の長さがmとnの長方形を考えます。
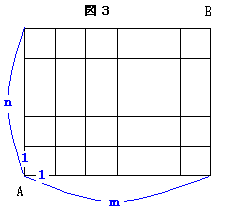
問5.(1)m、nがともに偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
(2)m、nがともに奇数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
(3)mが奇数、nが偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
<問題の出典は、数研出版が出している数研通信NO24の中にあったものです。>
皆さん、考え方がわかったら、全部でなくていいですから、とペンネームを添えて、メールで送ってください。待っています。
![]()
