�����Q�V�N�Q���W��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��31�U�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF1��1�P���`�Q���W����
�m�����̘a�ƍ��n
�F����I�����܂��Ă��߂łƂ��������܂��B2015�N���������������ڎ���܂��悤��낵�����肢�����܂��B
�O���R�Q�{�S�Q�|�T�Q�A�P���S�Q�{�V�Q�|�W�Q�A�Q���T�Q�{�P�P�Q�|�P�Q�Q�A�R���S�Q�{�U�Q�|�V�Q�E�E�E�̂悤�ɂR���̕����̘a�ƍ��ŕ\�����Ƃ��ł��܂��B
�������A���Q�{���Q�|���Q�@�́@��≨��≨���Ő������Ƃ���B
���P�F�S�C�T�C�U�C�V�����Q�{���Q�|���Q�i��≨��≨���Ő������j�̌`�ŕ\���Ă��������B
���Q�F��ʂɔC�ӂ̂O�ȏ�̐������@���Q�{���Q�|���Q�i��≨��≨���Ő������j�̌`�ŕ\����邩�ۂ����l�@���������B�@
���Q�l�����F���w�I�����s�b�N�ւ̓��R�@���_�̐��I104��i���q���X�j��
�uuchinyan�v
01/11 17��38���@��M
�uuchinyan�v
01/12 14��55���@��M
�uuchinyan�v
01/12 17��23���@��M
�uuchinyan�v
01/13 12��39���@��M
�uuchinyan�v
01/14 15��44���@��M �X�V 2/8
(�l�@1)�̓�����̈�Ƃ��Ď����܂����B
2n = (3n)^2 + (4n - 1)^2 - (5n - 1)^2
2n + 1 = (3n - 1)^2 + (4n - 4)^2 - (5n - 4)^2
���̂����C2n + 1 �̕��ŁC
n = 13 �̂Ƃ��C27 = 38^2 + 48^2 - 61^2
n = 55 �̂Ƃ��C111 = 164^2 + 216^2 - 271^2
�ƂȂ��āC���̗��ꂳ��̗���Č��ł��܂��B
�ǂ����C�w�i�̍P�����͂���̂悤�ł��ˁB
�uuchinyan�v
01/18 13��27���@��M �X�V 2/8
���P�F
4 = 5^2 + 10^2 - 11^2 = .7^2
+ 22^2 - 23^2 = ..
5 = 4^2 + 5^2 - 6^2 = 6^2 +
15^2 - 16^2 = ...
6 = 5^2 + 9^2 - 10^2 = 7^2 +
21^2 - 22^2 = ...
7 = 6^2 + 14^2 - 15^2 = 8^2 +
28^2 - 29^2 = ...
���Q�F
n = a^2 + b^2 - c^2�Cn �� 0 �ȏ�̐����Ca�Cb�Cc �� 0 < a < b < c �ƂȂ鐮��
����́C��ɉ\�ł��B�Ⴆ�C���̂悤�ɂ�������ł��傤�B
b = k�Cc = k + 1 �Ƃ��܂��B����ƁCb < c �ŁC
n = a^2 + k^2 - (k + 1)^2 =
a^2 - 2k - 1
a < b ���Ca < k�C- 2a > - 2k�C�ƂȂ��āC
n = a^2 - 2k - 1 < a^2 -
2a - 1�C(a - 1)^2 > n + 2�Ca > 1 + ��(n + 2)
�����ŁCm �� m > 1 + ��(n + 2) �ŁCn �������̂Ƃ� m ����Cn ����̂Ƃ� m �������C�Ɏ��C
a = m�Cb = k =
(m^2 - n - 1)/2�Cc = k + 1 = (m^2 - n + 1)/2�C�Ƃ��āC
a�Cb�Cc �� 0 < a < b < c �ƂȂ鐮���C�ŁC
a^2 + b^2 - c^2
= m^2 + ((m^2 - n - 1)/2)^2 -
((m^2 - n + 1)/2)^2
= m^2 + (((m^2 - n)^2 - 2(m^2
- n) + 1) - ((m^2 - n)^2 + 2(m^2 - n) + 1))/4
= m^2 + (- 4(m^2 - n))/4
= m^2 - (m^2 - n)
= n
�ƂȂ�܂��B
���̍\���@��薾�炩�ł����Cm �̎����͖����ɂ���̂ŁC�����Ȃ���͖����ɂ���܂��B
�܂��C�������Cb = k�Cc = k + d�Cd >= 1�C�œ��l�̂��Ƃ��l������̂ŁC
��蕡�G�ɂȂ�܂����C����ȊO�̍\�����\�ł��B
(�l�@1)
��C���Ƃ͗���܂����Cb = k�Cc = k + d�Cd �� 1 �ȏ�̐����C���l���Ă݂܂����B
���l�ɂ��āCa < b�Ca < k�C- 2da > - 2dk�C���C
n = a^2 + k^2 - (k + d)^2 =
a^2 - 2dk - d^2 < a^2 - 2da - d^2�C
(a - d)^2 > n + 2d^2�Ca > d + ��(n + 2d^2)
�����ŁCm �� m > d + ��(n + 2d^2) �Ɏ��C
a = m�Cb = k =
(m^2 - n - d^2)/(2d)�Cc = k + d = (m^2 - n + d^2)/(2d)
�������Cb�Cc �͐����Ȃ̂ŁC�^����ꂽ n �ɑ��� d �����߂��� m �����̂悤�ɑI�ԕK�v������܂��B
����͕K�������\�ł͂���܂���Bm^2 �� n + d^2 (mod 2d) �łȂ���Ȃ�܂���B
����͕�����]�Ƃ��Ēm���Ă���b�ł����C����b�͂����ł͂����ɗ�ōl���Ă݂܂��傤�B
d = 1 �̂Ƃ��́C��قnj����悤�ɁC���ׂĂ� n �ɑ��ĕK����������܂��B
n = 7�Cd = 5 �Ƃ��Ă݂܂��傤�B
����ƁCmod 10 �ŁCm^2 �� 7 + 25 �� 32 �� 2�C����͉�������܂���B
n = 7�Cd = 9 �ł́Cmod 18 �ŁCm^2 �� 7 +
81 �� 88 �� 16�Cm �� �}4�C�ŁC
m > 9 + ��(7 +
2(9^2)) = 9 + ��169 = 9 + 13 = 22�Cm = 32�C�Ƃł��āC
a = 32�Cb = (32^2 -
7 - 9^2)/18 = 52�Cc = 52 + 9 = 61�C
7 = 32^2 + 52^2 - 61^2
�Ə����܂��B
�u���̈��NO74�CNO2�F2015�N1��11���i��) �v�ɂ����C
���{����111���̘a�ƍ��ŕ\���ƁA111��164�O2�{432�O2�|541�O2�����藧���܂��B
���܂��A����27�N�͂Q�V��38�O2�{48�O2�|61�O2�Ƃ��ĕ\����܂��B
���C���̕��@�ōČ��ł��邩�C���ׂĂ݂܂��B
n = 27�Cd = 13�Cmod 26�Cm^2 �� 27 +
13^2 �� 196�Cm �� �}14�C
m > 13 + ��(27 +
2(13^2)) = 13 + ��365 = 13 + 19.1�c = 32.1�c�Cm = 38�C�Ƃł��āC
a = 38�Cb = (38^2 -
27 - 13^2)/26 = 48�Cc = 48 + 13 = 61�C
27 = 38^2 + 48^2 - 61^2
n = 111�Cd = 109�Cmod 218�Cm^2 �� 111 +
109^2 �� 11992 �� 2
����������̂͂��Ȃ����̂ł����Cm = 2x �Ƃ����ƁCmod 109 �ŁC
2x^2 �� 1�Cx^2 �� 55�Cmod 109 �� 109 �͑f��
�����ŁC������]�̒藝���g���Ē��ׂ�ƁC�ǂ������͂Ȃ��悤�ł��I
�������C
��111��164�O2�{432�O2�|541�O2�����藧���܂��B
�Ə�����Ă���̂ŁC���������Ȃ��C�Ǝv���āC�E�ӂ��v�Z���Ă݂�ƁC
164^2 + 432^2 - 541^2 = 26896
+ 186624 - 292681 = - 79161 �� 111
�ƂȂ��Ă��܂��܂����B�����L�ڃ~�X���ȁH
���̌�C����������܂����ˁB
�u���̈��NO74�CNO3�F2015�N1��12���i��)�v�ɂ����C
��111��164�O2�{216�O2�|271�O2�������ł��B
����Ȃ�D�D�D
n = 111�Cd = 55�Cmod 110�Cm^2 �� 111 +
55^2 �� 3136 �� 56
����������̂ɁCm = 2x �Ƃ����ƁCmod 55 �ŁC
2x^2 �� 28�Cx^2 �� 14�C����͒n���ɒ��ׂāCx
�� �}17,�}27�Cm �� �}34,�}54 mod 110
m > 55 + ��(111 +
2(55^2)) = 55 + ��6161 = 55 + 78.4�c = 133.4�c�Cm = 164�C�Ƃł��āC
a = 164�Cb = (164^2
- 111 - 55^2)/110 = 216�Cc = 216 + 55 = 271�C
111 = 164^2 + 216^2 - 271^2
�ƍČ��ł��܂��B
�������C����ȊO�ɂ������̉�������܂����C�܂��C����͂������Ƃɂ��܂��傤�B
������ɂ���C���̂悤�Ȏ����|���Ə�����Ƃ������Ƃ́C�w�i�ɉ�������܂��ˁB
���̌�ɁC�u���}�k�W�����v�C�u�P�����v�C�Ƃ����L�[���[�h������̂ŁC
�ނ��������P����������̂ł��傤���B
�����v���ăl�b�g�ŏ����T���Ă݂��̂ł����C������܂���ł����B
(�l�@2)
���p��͂��܂�Ӗ��͂���܂��C
��ɉ��̂��� d = 1 �̏ꍇ�����������P�����炵�������Ă����܂��傤���B
d = 1 �̏ꍇ�́C
m �� m > 1 +
��(n + 2) �ŁCn �������̂Ƃ� m ����Cn ����̂Ƃ� m �������C�Ɏ��C
a = m�Cb = k =
(m^2 - n - 1)/2�Cc = k + 1 = (m^2 - n + 1)/2
�ł����B�����ŁC
n �������̂Ƃ�
n -> 2n�Cm -> 2m
+ 1�C�ƒu��������ƁC
m > ��(2n + 2)/2
a = 2m + 1�Cb = k =
2m^2 + 2m - n �Cc = k + 1 = 2m^2 + 2m - n + 1
2n = (2m + 1)^2 + (2m^2 + 2m
- n)^2 - (2m^2 + 2m - n + 1)^2
n ����̂Ƃ�
n -> 2n + 1�Cm -> 2m�C�ƒu��������ƁC
m > (1 + ��(2n + 3))/2
a = 2m�Cb = k =
2m^2 - n - 1 �Cc = k + 1 = 2m^2 - n
2n + 1 = (2m)^2 + (2m^2 - n -
1)^2 - (2m^2 - n)^2
�Ə����܂��B
�����ŁC�Ⴆ�Cm = n + 2 �Ƃ���C���ׂĂ� 0 �ȏ�̐��� n �ŏ����̕s�����͐�������̂ŁC
2n = (2n + 5)^2 + (2n^2 + 9n
+ 12)^2 - (2n^2 + 9n + 13)^2
2n + 1 = (2n + 4)^2 + (2n^2 +
7n + 7)^2 - (2n^2 + 7n + 8)^2
�ƂȂ�܂��B
���́C2015�N1��12��(��)�ɁC���̗��ꂳ�烁�[�����C
��x�Ђ������玟�̍P�����̏������C�Ƃ���܂����B
���uA Collection of
Algebraic Identities�v�Ƃ����T�C�g�ɂ�
�������̍P�������Љ��Ă��܂��D
��https://sites.google.com/site/tpiezas/Home
�����̃T�C�g�Ŏ��̂悤�ȍP�����������܂����D
��2*n=(2*m+1)^2+(2*m^2+2*m-n)^2-(2*m^2+2*m-n+1)^2�C
��2*n-1=(2*m)^2+(2*m^2-n)^2-(2*m^2-n+1)^2�D
��(https://sites.google.com/site/tpiezas/003)
������2�̍P�����ɂ����ėႦ�� m=n+2 �Ƃ����
�����ꂪ���̂܂ܖ��2�̉ɂȂ��Ă��܂��D
�ŏ������Ƃ��ɂ́u��[�������Ȃ��v�Ǝv�����̂ł����C
�悭����ƁC����� d = 1 �̏ꍇ�ŁC���̎�@�Ŋ��ɓ����Ă���̂ł́C�Ǝv���m�F���Ă݂܂����B
�ŏ��̎��͑S�������ŁC�Q�Ԗڂ̎��͎��̎��� n
-> n - 1 �Ƃ������̂ł��ˁB
(�l�@3)
(�l�@1)�ł́C�^����ꂽ n �ƔC�ӂ� d �ɑ��� m �����߂���@���l���܂����B
����ɂ͎��̏������������K�v�����肵���B
m > d + ��(n + 2d^2)�Cm^2 �� n + d^2 (mod 2d)
�����ɉ�������ꍇ�ɂ́C
a = m�Cb = (m^2 -
n - d^2)/(2d)�Cc = b + d = (m^2 - n + d^2)/(2d)�C
n = a^2 + b^2 - c^2
�Ə����܂��B�������Ȃ���C�������݂��Ȃ����Ƃ�����܂����B
�����C���������́Cn = a^2 + b^2 -
c^2 �ƂȂ� a�Cb�Cc �� n �ŕ\����Ώ\���Ȃ̂ŁC
�^����ꂽ n �ɑ��ď����������悤�� d �� m �����߂�Ώ\���ł��B
���ہCd = 1 �̂Ƃ��͂��ꂪ�\�Ȃ��Ƃ���Q�F��(�l�@2)�Ŏ����܂����B
�����ł͈�ʂ� d �� 1 �ȊO���܂ޓ�������Ă݂܂��傤�B
n = 0 �̏ꍇ�́Ca�Cb�Cc �Ƃ��ăs�^�S���X���Ƃ�������ł��B
n = 1 �̏ꍇ�́C������Ƃ��܂������Ă��Ȃ��̂ŁC�ЂƂ܂��Cd = 1 �őË����܂� (^^;
�ȉ��ł́Cn >= 2 �Ƃ��܂��B
�܂��Cm^2 �� n + d^2 (mod 2d) ���l���܂��B
���Cs �� 0 �ȏ�̐����Ƃ��āCm = n + d + 2ds ���� m = d - n + 2ds �Ƃ��Ă݂܂��B
����ƁC�ǂ�����Cn^2 �� n�Cn(n - 1) �� 0 (mod
2d)�C�ƂȂ�܂��B
�����ŁCn(n - 1) �͏�ɋ����Ȃ̂ŁCn(n - 1) = 2d�Cd = n(n - 1)/2�C�ƌ��߂邱�Ƃ��ł��C
��������������̏����� n >= 2 �ŏ�ɖ������܂��B
���ɁCm > d + ��(n + 2d^2)�C���l���܂��B
(1) m = n + d + 2ds �̏ꍇ
n + d + 2ds > d + ��(n + 2d^2)�Cn + 2ds > ��(n + 2d^2)
���炩�ɁCn >= 2�Cs >= 1 �ŏ�ɐ������܂��B�����ŁCn >= 2�Cs >= 1�C�ŁC
a = n + (2s + 1)d = (s +
1/2)n^2 - (s - 1/2)n
b = ((n + (2s + 1)d)^2 - n -
d^2)/(2d) = (2s + 1)n + (2s^2 + 2s)d + 1 = s(s + 1)n^2 - (s^2 - s - 1)n + 1
c = b + d = (2s + 1)n + (2s^2
+ 2s + 1)d + 1 = (s^2 + s + 1/2)n^2 - (s^2 - s - 1/2)n + 1
n = ((s + 1/2)n^2 - (s -
1/2)n)^2 + (s(s + 1)n^2 - (s^2 - s - 1)n + 1)^2 - ((s^2 + s + 1/2)n^2 - (s^2 -
s - 1/2)n + 1)^2
(2) m = d - n + 2ds �̏ꍇ
d - n + 2ds > d + ��(n + 2d^2)�C- n + 2ds > ��(n + 2d^2)�Cs > (n + ��(n + 2d^2))/(2d)
���͈̔͂� n�Cs �ɑ��āC
a = - n + (2s + 1)d = (s +
1/2)n^2 - (s + 3/2)n
b = ((- n + (2s + 1)d)^2 - n
- d^2)/(2d) = - (2s + 1)n + (2s^2 + 2s)d + 1 = s(s + 1)n^2 - (s^2 + 3s + 1)n +
1
c = b + d = - (2s + 1)n +
(2s^2 + 2s + 1)d + 1 = (s^2 + s + 1/2)n^2 - (s^2 + 3s + 3/2)n + 1
n = ((s + 1/2)n^2 - (s +
3/2)n)^2 + (s(s + 1)n^2 - (s^2 + 3s + 1)n + 1)^2 - ((s^2 + s + 1/2)n^2 - (s^2 +
3s + 3/2)n + 1)^2
�������Cn = 2 �̏ꍇ�ɂ́Cd = 1 �ƂȂ�܂��B
����͏������G�Ȃ̂ŁC���������Ȍ��Ȏ������߂Ă݂܂��傤�B
��قǂ́Cn(n - 1) �� 0 (mod 2d)�C�ɂ����āCt ��
0 �ȏ�̎��R���Ƃ��Ď��̂悤�ɂł��܂��B
(1) m = n + d + 2ds �̏ꍇ
(1-1) n �������Cn = 2t�C�̏ꍇ
n = 2d�Cd = t �ƌ��߂邱�Ƃ��ł��C��������������� n >= 2 �ŏ�ɐ������܂��B
�����āCm = n + d + 2ds = 3t +
2st�C�ł��B
���ɁCm > d + ��(n + 2d^2)�C���l���܂��B
3t + 2st > t + ��(2t + 2t^2)�C2t + 2st > ��(2t + 2t^2)
���炩�ɁCn = 2t >= 2�Cs >= 1 �ŏ�ɐ������܂��B�����ŁCn >= 2�Cs >= 1�C�ŁC
a = 3t + 2st = (2s + 3)t
b = (((2s + 3)t)^2 - 2t -
t^2)/(2t) = (2s^2 + 6s + 4)t - 1
c = b + t = (2s^2 + 6s + 5)t
- 1
n = 2t = ((2s + 3)t)^2 +
((2s^2 + 6s + 4)t - 1)^2 - ((2s^2 + 6s + 5)t - 1)^2
�������Cn = 2 �̏ꍇ�ɂ́Cd = 1 �ƂȂ�܂��B
(1-2) n ����Cn = 2t +
1�C�̏ꍇ
n - 1 = 2d�Cd = t �ƌ��߂邱�Ƃ��ł��C��������������� n >= 3 �ŏ�ɐ������܂��B
�����āCm = n + d + 2ds = 3t +
1 + 2st�C�ł��B
���ɁCm > d + ��(n + 2d^2)�C���l���܂��B
3t + 1 + 2st > t + ��(2t + 1 +
2t^2)�C2t + 1 + 2st > ��(2t +
1 + 2t^2)
���炩�ɁCn = 2t + 1 >= 3�Cs >= 1 �ŏ�ɐ������܂��B�����ŁCn >= 3�Cs >= 1�C�ŁC
a = 3t + 1 + 2st = (2s + 3)t
+ 1
b = (((2s + 3)t + 1)^2 - (2t
+ 1) - t^2)/(2t) = (2s^2 + 6s + 4)t + (2s + 2)
c = b + t = (2s^2 + 6s + 5)t
+ (2s + 2)
n = 2t + 1 = ((2s + 3)t +
1)^2 + ((2s^2 + 6s + 4)t + (2s + 2))^2 - ((2s^2 + 6s + 5)t + (2s + 2))^2
�������Cn = 3 �̏ꍇ�ɂ́Cd = 1 �ƂȂ�܂��B
(2) m = d - n + 2ds �̏ꍇ
(2-1) n �������Cn = 2t�C�̏ꍇ
n = 2d�Cd = t �ƌ��߂邱�Ƃ��ł��C��������������� n >= 2 �ŏ�ɐ������܂��B
�����āCm = d - n + 2ds = - t
+ 2st�C�ł��B
���ɁCm > d + ��(n + 2d^2)�C���l���܂��B
- t + 2st > t + ��(2t + 2t^2)�Cs > (2t + ��(2t^2 + 2t))/(2t)�Ct > 1/(2(s - 1)^2 - 1)
�����͈̔͂� s�Ct �ɑ��āC
a = - t + 2st = (2s - 1)t
b = (((2s - 1)t)^2 - 2t -
t^2)/(2t) = (2s^2 - 2s)t - 1
c = b + t = (2s^2 - 2s + 1)t
- 1
n = 2t = ((2s - 1)t)^2 +
((2s^2 - 2s)t - 1)^2 - ((2s^2 - 2s + 1)t - 1)^2
�������Cn = 2 �̏ꍇ�ɂ́Cd = 1 �ƂȂ�܂��B
(2-2) n ����Cn = 2t +
1�C�̏ꍇ
n - 1 = 2d�Cd = t �ƌ��߂邱�Ƃ��ł��C��������������� n >= 3 �ŏ�ɐ������܂��B
�����āCm = d - n + 2ds = - t
+ 2st - 1�C�ł��B
���ɁCm > d + ��(n + 2d^2)�C���l���܂��B
- t + 2st - 1 > t + ��(2t + 1 +
2t^2)�Cs > (2t + 1 + ��(2t^2 +
2t + 1))/(2t)�Ct > (2(s - 1) + 1)/(2(s - 1)^2 - 1)
�����͈̔͂� s�Ct �ɑ��āC
a = - t + 2st - 1 = (2s - 1)t
- 1
b = (((2s - 1)t - 1)^2 - (2t
+ 1) - t^2)/(2t) = (2s^2 - 2s)t - 2s
c = b + t = (2s^2 - 2s + 1)t
- 2s
n = 2t + 1 = ((2s - 1)t - 1)^2
+ ((2s^2 - 2s)t - 2s)^2 - ((2s^2 - 2s + 1)t - 2s)^2
�������Cn = 3 �̏ꍇ�ɂ́Cd = 1 �ƂȂ�܂��B
�܂Ƃ߂�ƁC�K�� s�Ct �͈̔͂ŁC
2t = ((2s + 3)t)^2 + ((2s^2 +
6s + 4)t - 1)^2 - ((2s^2 + 6s + 5)t - 1)^2
2t + 1 = ((2s + 3)t + 1)^2 +
((2s^2 + 6s + 4)t + (2s + 2))^2 - ((2s^2 + 6s + 5)t + (2s + 2))^2
����
2t = ((2s - 1)t)^2 + ((2s^2 -
2s)t - 1)^2 - ((2s^2 - 2s + 1)t - 1)^2
2t + 1 = ((2s - 1)t - 1)^2 +
((2s^2 - 2s)t - 2s)^2 - ((2s^2 - 2s + 1)t - 2s)^2
���ɁC�����̎��ŁC
s = 1
2t = (5t)^2 + (12t - 1)^2 -
(13t - 1)^2�Ct >= 1
2t + 1 = (5t + 1)^2 + (12t +
4)^2 - (13t + 4)^2�Ct >= 1
s = 2
2t = (7t)^2 + (24t - 1)^2 -
(25t - 1)^2�Ct >= 1
2t + 1 = (7t + 1)^2 + (24t +
6)^2 - (25t + 6)^2�Ct >= 1
����
2t = (3t)^2 + (4t - 1)^2 -
(5t - 1)^2�Ct >= 2
2t + 1 = (3t - 1)^2 + (4t -
4)^2 - (5t - 4)^2�Ct >= 4
s = 3
2t = (9t)^2 + (40t - 1)^2 -
(41t - 1)^2�Ct >= 1
2t + 1 = (9t + 1)^2 + (40t +
8)^2 - (41t + 8)^2�Ct >= 1
����
2t = (5t)^2 + (12t - 1)^2 -
(13t - 1)^2�Ct >= 1
2t + 1 = (5t - 1)^2 + (12t -
6)^2 - (13t - 6)^2�Ct >= 1
�D�D�D
�����āCs = 2 ��
2t + 1 = (3t - 1)^2 + (4t - 4)^2
- (5t - 4)^2�Ct >= 3
�ɂ����āC
t = 13�C27 = 38^2 +
48^2 - 61^2
t = 55�C111 = 164^2
+ 216^2 - 271^2
�ƂȂ��āC���̗��ꂳ��́u���̈���v�ɂ���Ⴊ�Č��ł��܂��B
�w�i�ɂ������̂͂��̕s�����ł��ˁB
(���z)
�ŏ��͖��ɊȒP�Ɏv���C��ӂ����Ⴂ���Ă��Ȃ���������ƐS�z�������肵�܂����B
���̌�C���̗��ꂳ��Ƃ̃��[���̂����ŁC��ӂ̗����͐��������̂́C
�ނ���C�w�i�ɂ���P������T�����Ƃɋ������킢�Ă��āC
(�l�@1)�̍Ō�ɏ������悤�ɁC��ʂ̉���^����P������T���̂��ۑ�ɂȂ�܂����B
���ہCd = 1 �̏ꍇ��(�l�@2)�Ŏ������悤�ɗe�ՂɍP�������܂��B
d �� 1 �ȊO�̏ꍇ���C�ꕔ�ł����C(�l�@3)�Ŏ������Ƃ��ł��܂����B
�����C����Ɉ�ʂ� d �̏ꍇ�́C
m > d + ��(n + 2d^2)�Cm^2 �� n + d^2 (mod 2d)
�ɉ�������ꍇ�ɂ́C
a = m�Cb = (m^2 -
n - d^2)/(2d)�Cc = b + d = (m^2 - n + d^2)/(2d)�C
n = a^2 + b^2 - c^2
�Ə����܂����C�������݂��Ȃ����Ƃ�����܂��B
��������l�߂�̂́C���ɂ͓�����ŁC������Ǝv���t���Ȃ��ł� (^^;
�Ȃ��C���Ȃ݂ɁC�Ⴆ�C�������P�����̂��������g���āC
27
= 8^2 + 18^2 - 19^2
= 1026^2 + 1324^2 - 1675^2
= 66^2 + 160^2 - 173^2
= 92^2 + 318^2 - 331^2
= 38^2 + 48^2 - 61^2
= �c
2015
= 46^2 + 50^2 - 51^2
= 6085300^2 + 8110376^2 -
10139481^2
= 5036^2 + 12088^2 - 13095^2
= 7050^2 + 24174^2 - 25181^2
= 3020^2 + 4024^2 - 5031^2
= �c
�ȂǂƂƏ����܂��ˁB
�u�Ӱ��݁v
01/11 21��20���@��M �X�V 2/8
��
���2��������ċ��߂�B
���Q�F��ʂɔC�ӂ̂O�ȏ�̐������@���Q�{���Q−���Q�i��≨��≨���Ő������j�̌`�ŕ\����邩�ۂ����l�@���������B
c-b=k,
c+b=2b+k
a^2-k(2b+k)=a^2-k^2-2bk=b^2�E�E�Ea<b �Ȃ̂Łc2��b
a^2=(k+b)^2
�@b=2�E�E�E(k+2)^2-k(4+k)
�@k=1�E�E�E3^2-(4+1)=4
�@k=2�E�E�E4^2-2(4+2)=4
�������͕\���邱�Ƃ͂킩�邪�c
k=1�̂Ƃ����l����Ɓc
�ȉ��̂悤�ɂ��ׂĂ̏ꍇ�ʼn\�Ȃ��Ƃ��킩��
^^
a^2-(2b+1)=m
a^2=2b+1+m
�͂��ł����݂ł���c
m�������Ȃ�Aa�͊=(2n-1)�@
(2n-1)^2=(2b+1)+m�E�E�Em�͋���
(4n^2-4n-m)/2=b
m����Ȃ�ca�͋���=2n
(2n)^2=(2b+1)+m�cb=(4n^2-1-m)/2
�Em=4�Ȃ�c
(2n-1)^2=2b+5�cb=(4n^2-4n-4)/2=2n^2-2n-2
2n-1<2n^2-2n-2
4n+1<2n^2�cn=3 �͖������c
5^2+10^2-11^2=4
�E m=5
�Ȃ�c
(2n)^2=2b+6�cb=(4n^2-6)/2=2n^2-3
2n<2n^2-3�cn=2 �͖������c
4^2+5^2-6^2=5
�E m=6
�Ȃ�c
(2n-1)^2=2b+7�cb=(4n^2-4n-6)/2=2n^2-2n-3
2n-1<2n^2-2n-3
4n+2<2n^2�cn=3 �͖������c
5^2+9^2-10^2=6
�E m=7
�Ȃ�c
(2n)^2=2b+8�cb=(4n^2-8)/2=2n^2-4
2n<2n^2-4�cn=3 �͖������c
6^2+14^2-15^2=7
����͎��M���� ^^��
�u��x�Ђ����v 01/12 08��10���@��M
�X�V 2/8
�y���l�[���F��x�Ђ�����
��316�w�I�ȉ�����̉𑗂�܂��D
��낵�����肢�������܂��D
���1�F
4=19^2+178^2-179^2
5=28^2+389^2-390^2
6=39^2+757^2-758^2
7=52^2+1348^2-1349^2 (��)
���2�F
�C�ӂ̐����́Ca^2+b^2-c^2 (a�Cb�Cc �͐������ł����āCa��b��c����)
�Ƃ����`�ɕ\�����Ƃ��\�ł���D(��)
�ȉ��Ɏ����悤�ɁC�C�ӂ̐��� n �́C�����̘a�ƍ��̌`�ɂ�����D
n = (n^2+3)^2 + (3*n^2+4+(1/2)*(n^4-n))^2 - (3*n^2+5+(1/2)*(n^4-n))^2�D
�����ŁCn^2+3�C3*n^2+4+(1/2)*(n^4-n)�C3*n^2+5+(1/2)*(n^4-n) �͂��ׂ�
���̐����ł��邱�Ƃ��킩��D
�܂��C�s���� n^2+3 ��
3*n^2+4+(1/2)*(n^4-n) �� 3*n^2+5+(1/2)*(n^4-n)
�����藧���Ă��邱�Ƃ��킩��D
����ĔC�ӂ̐��� n �́C
n=a^2+b^2-c^2 (a�Cb�Cc�͐������ł����āCa��b��c����)
�Ƃ����`�ɂ����邱�Ƃ��������D
���2�ɂ��āF
��蕶�́u�C�ӂ�0�ȏ�̐����v�ƂȂ��Ă��܂����C���ۂɂ́C��ɏq�ׂ��悤��
�u�C�ӂ̐����v�� a^2+b^2-c^2 (0��a��b��c) �Ƃ����`�ɂ�����Ǝv���܂��D
�C�ӂ̐���n�ɑ��āCy^2-n ��4�ȏ�̋����ɂȂ�悤�Ȑ�����y��(������)���݂��܂��D
������ y^2-n=2*x (x��2�ȏ�̐���)�Ƃ��Ă����C
�P���� n=(1+y)^2+(x+y)^2-(1+x+y)^2 �����藧���܂��D
y=n^2+2 �Ƃ������̂���L�̉ł��D
�uA Collection of Algebraic Identities�v�Ƃ����T�C�g�ɂ�
�����̍P�������Љ��Ă��܂��D
https://sites.google.com/site/tpiezas/Home
���̃T�C�g�Ŏ��̂悤�ȍP�����������܂����D
2*n=(2*m+1)^2+(2*m^2+2*m-n)^2-(2*m^2+2*m-n+1)^2�C
2*n-1=(2*m)^2+(2*m^2-n)^2-(2*m^2-n+1)^2�D
(https://sites.google.com/site/tpiezas/003)
����2�̍P�����ɂ����ėႦ��
m=n+2 �Ƃ����
���ꂪ���̂܂ܖ��2�̉ɂȂ��Ă��܂��D
�u�l�c�����v
01/14 13��25���@��M �X�V 2/8
���Q���ŏ��ɉ����D
�@���Q�{���Q�|���Q�����C���C���C���͐������C�����������C���͔����Ƃ���D
i). �����Q���i���͔����j�̂Ƃ��C
�@�����Q���{�P�i���͔����j�Ƃ���ƁC
�@�@���Q�|���Q�����Q�|����(�Q���{�P)�Q�|�Q��
�@�@��(���{��)(���|��)���S���Q�{�S���{�P�|�Q��
�@�����ŁC
�@�@���{�����S���Q�{�S���{�P�|�Q���C���|�����P
�Ƃ���ƁC
�@�@�����Q���Q�{�Q���{�P�|���C�����Q���Q�{�Q���|��
�@���炩�ɁC�������ł���C
�@�@���|����(�Q���Q�{�Q���|��)�|(�Q���{�P)���Q���Q�|���|�P
�@�������ł��邩��C
�@�@�Q���Q�|���|�P���O
�@�@�����Q��(���{�P)�^�Q
�@�����O����C����{(���{�P)�^�Q}�P�^�Q��(���{�Q)�P�^�Q�^�Q
�@���̂Ƃ��C���������C���C���͑��݂���D
ii). �����Q���{�P�i���͔����j�̂Ƃ��C
�@�����Q���i���͐������j�Ƃ���ƁC
�@�@���Q�|���Q�����Q�|����(�Q��)�Q�|(�Q���{�P)
�@�@��(���{��)(���|��)���S���Q�|�Q���|�P
�@�����ŁC
�@�@���{�����S���Q�|�Q���|�P�C���|�����P
�Ƃ���ƁC
�@�@�����Q���Q�|���C�����Q���Q�|���|�P
�@���炩�ɁC�������ł���C
�@�@���|����(�Q���Q�|���|�P)�|�Q�����Q���Q�|�Q���|(���{�P)
�@�������ł��邩��C
�@�@�Q���Q�|�Q���|(���{�P)���O
�@�@������{�P�|(�Q���{�R)�P�^�Q}�^�Q�C{�P�{(�Q���{�R)�P�^�Q}�^�Q����
�@�����ŁC�����O����C(�Q���{�R)�P�^�Q����R���P
�@�@��{�P�|(�Q���{�R)�P�^�Q}�^�Q���O�C{�P�{(�Q���{�R)�P�^�Q}�^�Q��(�P�{��R)�^�Q���O
�@�����O����C����{�P�{(�Q���{�R)�P�^�Q}�^�Q��{�P�{(���{�Q)�P�^�Q}�^�Q
�@���̂Ƃ��C���������C���C���͑��݂���D
�@�܂Ƃ߂�ƁC�ȉ��̂Ƃ��C���������C���C�������݂���D
�@�@���������̂Ƃ��C(���C���C��)��(�Q���{�P�C�Q���Q�{�Q���|���^�Q�C�Q���Q�{�Q���{�P�|���^�Q)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����(���{�Q)�P�^�Q�^�Q�C���͐����j
�@�@������̂Ƃ��C(���C���C��)��(�Q���C�Q���Q�|(���{�P)�^�Q�C�Q���Q�|(���|�P)�^�Q)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����{�P�{(���{�Q)�P�^�Q}�^�Q�C���͐����j
���P
�@���Q���C�����S�̂Ƃ��C������U�^�Q
�@�@�������Q
�@�@��(���C���C��)��(�T�C�P�O�C�P�P)�C(�V�C�Q�Q�C�Q�R)�C(�X�C�R�W�C�R�X)�C�c�c�c
�@�����T�̂Ƃ��C����(�P�{��V)�^�Q
�@�@�������Q
�@�@��(���C���C��)��(�S�C�T�C�U)�C(�U�C�P�T�C�P�U)�C(�W�C�Q�X�C�R�O)�C�c�c�c
�@�����U�̂Ƃ��C������Q
�@�@�������Q
�@�@��(���C���C��)��(�T�C�X�C�P�O)�C(�V�C�Q�P�C�Q�Q)�C(�X�C�R�V�C�R�W)�C�c�c�c
�@�����V�̂Ƃ��C�����Q
�@�@�������R
�@�@��(���C���C��)��(�U�C�P�S�C�P�T)�C(�W�C�Q�W�C�Q�X)�C(�P�O�C�S�U�C�S�V)�C�c�c�c
�@�܂Ƃ߂�ƁC
�@�@�S���T�Q�{�P�O�Q�|�P�P�Q���V�Q�{�Q�Q�Q�|�Q�R�Q���X�Q�{�R�W�Q�|�R�X�Q���c�c�c
�@�@�T���S�Q�{�T�Q�|�U�Q���U�Q�{�P�T�Q�|�P�U�Q���W�Q�{�Q�X�Q�|�R�O�Q���c�c�c
�@�@�U���T�Q�{�X�Q�|�P�O�Q���V�Q�{�Q�P�Q�|�Q�Q�Q���X�Q�{�R�V�Q�|�R�W�Q���c�c�c
�@�@�V���U�Q�{�P�S�Q�|�P�T�Q���W�Q�{�Q�W�Q�|�Q�X�Q���P�O�Q�{�S�U�Q�|�S�V�Q���c�c�c
�u�l�c�����v
01/15 13��59���@��M
�u�l�c�����v
01/30 11��13���@��M �X�V 2/8
�@���
�@�@�P�P�P���P�U�S�Q�{�Q�P�U�Q�|�Q�V�P�Q
����C������悤�ɁC
�@�@���{�P����
�ł�����͑��݂���D
�@���̉�@�ł́C
�@�@���{�P����
��O��ɉ����Ă���C���̏ꍇ�̉��͂��ׂċ��߂��D
�@���{�P�����̏ꍇ�ɂ��čl���Ă݂�D
�@�O��̂d���������̃}�N����
�@�@c>b
�̕�����
�@�@c>b+1
�Ƃ��邾���ł悢�D
�@�O�������P�O�O�O�͈̔͂ł́C���ׂĂ̂��ɂ��āC���C���C�������Ȃ��Ƃ��P�g���݂��邱�Ƃ�������D
�@�@(n,a,b,c)=(0,6,8,10),(1,7,11,13),(2,25,41,48),(3,12,22,25),(4,6,7,9),
�@�@�@�@�@�@�@(5,7,10,12),(6,9,11,14),(7,10,14,17),(8,8,13,15),(9,7,9,11),
�@�@�@�@�@�@�@(10,11,17,20),(11,14,16,21),(12,8,12,14),(13,7,8,10),(14,17,25,30),
�@�@�@�@�@�@�@(15,12,20,23),(16,8,11,13),(17,9,15,17),(18,15,33,36),(19,10,12,15),20,8,10,12),
...
�@���|���̒l�͂��낢�둶�݂��C�c�O�Ȃ���C�܂��K�����͌����o���Ă͂��Ȃ��D
�@���Q�{���Q�|���Q�����C���C���C���͐������C�����������C���͔����Ƃ���D
�@�@�����Q�|���Q�����Q�|��
�@�@��(���{��)(���|��)�����Q�|��
�@�����ŁC���Q�|���������i���C���͐������C�������j�Ƃ���D
�@���{�������|������C
�@�@���{�������C���|������
�@�@��(���C��)��((���{��)�^�Q�C(���|��)�^�Q)
�@����(���|��)�^�Q���O����C������
�@(���{��)�^�Q�C(���|��)�^�Q�������Ȃ̂ŁC
�@�@���C���̋��͈�v����
�@���Q�|���������C�����O����C
�@�@����(���{����)�P�^�Q
�@����(���{��)�^�Q��(���|��)�^�Q�����ł���C
�@�@����(���{����)�P�^�Q��(���|��)�^�Q����
�@�@���S(���{����)��(���|��)�Q
�@�@������(���Q�|�U�����{���Q)�^�S
�@�܂Ƃ߂�ƁC���C���͐������C�������C���C���̋���v���C
�@�@(���{����)�P�^�Q
���������ł���i���{�����͕������j�C
�@�@����(���Q�|�U�����{���Q)�^�S
�̂Ƃ��C
�@�@(���C���C��)��((���{����)�P�^�Q�C(���|��)�^�Q�C(���{��)�^�Q)
�ƂȂ�D
�@�����O�̂Ƃ��C
�@�@���C���͐������C�������C���C���̋���v�C�����͕������C�O�����Q�|�U�����{���Q
�ł��邩��C
�@�@(���C��)��(�X�C�P)�C(�Q�T�C�P)�C(�S�X�C�P)�C�E�E�E�C
�@�@�@�@�@�@�@(�P�W�C�Q)�C(�R�Q�C�Q)�C�E�E�E
�Ȃǂ̉������݂���D
�@����(���Q�|�U�����{���Q)�^�S����C
�@�@��(���|�U��)�{(���Q�|�S��)���O
�@�̂ɂ����U�����U�E�Q���P�^�Q�C���{�����͕������C���C���̋���v�ƂȂ�悤�ɐ��������C����I�ׂ悢�D
�@�������C���̂悤�Ȃ��C�����m���ɑ��݂��邩�ǂ����܂ł͕�����Ȃ��D
�@�S�̕������̘a�ɂ��āD
�@�d���������̃}�N���Ōv�Z�������Ƃ���C
2015=12+32+182+412=...=192+212+222+272
(61�ʂ�)
20152015=12+22+10812+43572=...=22142+22272+22292+23072
(572604�ʂ�)
�Ƃ�����ʂ̓������ꂽ�D
�u���N���̂�������v
01/18 16��57���@��M �X�V 2/8
![]()
�������Aa��b��c�An��0�Ƃ��܂��B
��n��0�̂Ƃ��́A3��a�Ab�Ac�̓s�^�S���X���ɂȂ�܂��B
 �@p�Aq�𐳂̐����Ƃ��āA����3���ł��B
�@p�Aq�𐳂̐����Ƃ��āA����3���ł��B
p2�|q2�A2pq�Ap2�{q2�@ (p��q)
�@p2�|q2��2pq�Ƃ���ƁA![]() �Ȃ̂�
�Ȃ̂�
�@p��![]() �̂Ƃ��́Aa��p2�|q2�A����2pq�Ac��p2�{q2
�̂Ƃ��́Aa��p2�|q2�A����2pq�Ac��p2�{q2
�@p��![]() �̂Ƃ��́Aa��2pq�A����p2�|q2�Ac��p2�{q2
�̂Ƃ��́Aa��2pq�A����p2�|q2�Ac��p2�{q2
��n��0�̏ꍇ�ׂ܂��B
���P
�����ŁAc��b�Ƃ̍���d �Ƃ����܂��B(c��b�{d�Ad��0)
����ƁA
![]()
![]()
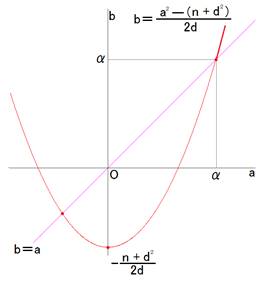
2�s�ڂ̎���b�ɂ��ĉ����܂��B
![]() �@����(1)
�@����(1)
���̃O���t�͉E�̂悤�ɂȂ�܂��B
a��b�Ȃ̂ŁA�������̉E��̑����Ԑ��������ΏۂɂȂ�܂��B
��(1)�ŁAa��b�����Ƃ����܂��B
![]()
![]()
![]()
����āA
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�Ec��b�Ƃ̍�d��1�̂Ƃ��A
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
![]() �@����(2)
�@����(2)
�Ȃ̂ŁAb�������̂Ƃ��A���q��2�̔{���ł��B
n����Ȃ�a�͋����An�������Ȃ�a�͊�ł��B
�@n��4�Ȃ�A![]() �Ȃ̂ŁAa��5�A7�A9�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��5�A7�A9�A����Ȃǂ��K���܂��B
�@��(2)�ɑ�����āA(a,b,c)�́A(5,10,11)�A(7,22,23)�A(9,38,39)�A����A
��ʂɂ́Ap��3�Ƃ��āA(2p�|1, 2p2�|2p�|2, 2p2�|2p�|1)
�@n��5�Ȃ�A![]() �Ȃ̂ŁAa��4�A6�A8�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��4�A6�A8�A����Ȃǂ��K���܂��B
�@��(2)�ɑ�����āA(a,b,c)�́A(4,5,6)�A(6,15,16)�A(8,29,30)�A���
��ʂɂ́Ap��3�Ƃ��āA(2p, 2p2�|3, 2p2�|2)
�@n��6�Ȃ�A![]() �Ȃ̂ŁAa��5�A7�A9�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��5�A7�A9�A����Ȃǂ��K���܂��B
�@��(2)�ɑ�����āA(a,b,c)�́A(5,9,10)�A(7,21,22)�A(9,37,38)�A���
��ʂɂ́Ap��3�Ƃ��āA(2p�|1, 2p2�|2p�|3, 2p2�|2p�|2)
�@n��7�Ȃ�A![]() �Ȃ̂ŁAa��6�A8�A10����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��6�A8�A10����Ȃǂ��K���܂��B
�@��(2)�ɑ�����āA(a,b,c)�́A(6,14,15)�A(8,28,29)�A(10,46,47)�A���
��ʂɂ́Ap��3�Ƃ��āA(2p, 2p2�|4, 2p2�|3)
�Ed��2�̂Ƃ��A
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
![]() �@����(3)
�@����(3)
�@�Ȃ̂ŁA���q��4�̔{���ł��B
�@(4p)2��16p2��4�~4p2�A
(4p�{1)2��16p2�{8p�{1��4�~(4p2�{2p)�{1�A
(4p�{2)2��16p2�{16p�{4��4�~(4p2�{4p�{1)�A
(4p�{3)2��16p2�{24p�{9��4�~(4p2�{6p�{2)�{1�A
�Ȃ̂ŁAn��4k�A4k�{1�̌`�̐��łȂ��Ƃ��܂������܂���B
n��4k �Ȃ�A
a��4p�Ƃ��āA ![]() �A
�A![]()
a��4p�{2�Ƃ��āA ![]() �A
�A
![]() �A
�A
n��4k�{1�Ȃ�A
a��4p�{1�Ƃ��āA ![]() �A
�A![]()
a��4p�{3�Ƃ��āA ![]() �A
�A![]()
�@�Ɛ����ɂȂ�܂����An��4k�{2�A4k�{3�̌`�̐��ł́Ab�������ɂ͂Ȃ�܂���B
�@n��4�Ȃ�A![]() �Ȃ̂ŁAa��6�A8�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��6�A8�A����Ȃǂ��K���܂��B
�@��(3)�ɑ�����āA(a,b,c)�́A(6,7,9)�A(8,14,16)�A���
�@n��5�Ȃ�A![]() �Ȃ̂ŁAa��7�A9�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��7�A9�A����Ȃǂ��K���܂��B
�@��(3)�ɑ�����āA(a,b,c)�́A(7,10,12)�A(9,18,20)�A���
�@n��6�A7�͂��܂������܂���B
�Ed��3�̂Ƃ��A
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
![]() �@����(4)
�@����(4)
�@�Ȃ̂ŁA���q��6�̔{���ł��B
(6p)2��36p2��6�~6p2�A
(6p�{1)2��36p2�{12p�{1��6�~(4p2�{2p)�{1�A
(6p�{2)2��36p2�{24p�{4��6�~(4p2�{4p)�{4�A
(6p�{3)2��36p2�{369p�{9��6�~(4p2�{6p�{1)�{3�A
(6p�{4)2��36p2�{48p�{16��6�~(4p2�{4p�{2)�{4�A
(6p�{5)2��36p2�{60p�{25��6�~(4p2�{6p�{4)�{1�A
�Ȃ̂ŁAn��6k�{3�A6k�{4�A6k�A6k�{1�̌`�̐��łȂ��Ƃ��܂������܂���B
n��6k�{3 �Ȃ�A
a��6p�Ƃ��āA ![]() �A
�A![]()
n��6k�{4�Ȃ�A
a��6p�{1�Ƃ��āA ![]() �Ac
�Ac![]()
a��6p�{5�Ƃ��āA ![]() �A
�A![]()
n��6k �Ȃ�A
a��6p�{3�Ƃ��āA ![]() �A
�A![]()
n��6k�{1�Ȃ�A
a��6p�{2�Ƃ��āA ![]() �A
�A![]()
a��6p�{4�Ƃ��āA ![]() �A
�A![]()
�@�Ɛ����ɂȂ�܂����An��6k�{2�A6k�{5�̌`�̐��ł́Ab�������ɂ͂Ȃ�܂���B
�@n��4�Ȃ�A![]() �Ȃ̂ŁAa��11�A13�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��11�A13�A����Ȃǂ��K���܂��B
�@��(4)�ɑ�����āA(a,b,c)�́A(11,18,21)�A(13,26,29)�A���
n��6�Ȃ�A![]() �Ȃ̂ŁAa��9�A15�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��9�A15�A����Ȃǂ��K���܂��B
�@��(4)�ɑ�����āA(a,b,c)�́A(9,11,14)�A(15,35,38)�A���
�@n��7�Ȃ�A![]() �Ȃ̂ŁAa��10�A14�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��10�A14�A����Ȃǂ��K���܂��B
�@��(4)�ɑ�����āA(a,b,c)�́A(10,14,17)�A(14,30,33)�A���
�@n��5�A8�͂��܂������܂���B
�@n��9�Ȃ�A![]() �Ȃ̂ŁAa��12�A18�A����Ȃǂ��K���܂��B
�Ȃ̂ŁAa��12�A18�A����Ȃǂ��K���܂��B
�@��(4)�ɑ�����āA(a,b,c)�́A(12,21,24)�A(18,51,54)�A���
���Q�i�����܂��Ȃ��b�Ƃ��āj
�����ŁAn��4�A5�A6�A7�������܂��B
�Ec��b�̍���d�̂Ƃ��A
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
![]() �@����(5)
�@����(5)
�@�Ȃ̂ŁA���q��2d�̔{���ł��B
�@��̓I��n�����܂�ƁAa�̏����ׂ邱�Ƃ��ł��܂��B
���Ⴆ�An��2015(��5�~13�~31)�Ƃ��Ă݂܂��B
�@d�Ƃ��ẮAn�̖��l���₷���̂ŁAd��5�Ƃ��Ă݂܂��B
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�@2d��10�Ȃ̂ŁA10�̔{��a��60�����ɂ��A��(5)�ɑ�����Ă݂܂��B
����ƁAa��60�A![]() �Ac��161
�Ac��161
�@���ɁAd��13�Ƃ��Ă݂܂��B
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�@2d��26�Ȃ̂ŁA26�̔{��a��78�����ɂ��A��(5)�ɑ�����Ă݂܂��B
����ƁAa��78�A![]() �Ac��163
�Ac��163
�@���ɁAd��31�Ƃ��Ă݂܂��B
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�@2d��62�Ȃ̂ŁA62�̔{��a��124�����ɂ��A��(5)�ɑ�����Ă݂܂��B
����ƁAa��124�A![]() �Ac��231
�Ac��231
��
���̗�́An��d����Ȃ̂ł��܂������܂��B
�����ɁAn��2016(��25�~32�~7)�Ƃ��Ă݂܂��B
�@d��7�Ƃ��Ă݂܂��B
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�@2d��14�Ȃ̂ŁA14�̔{��a��56�����ɂ��A��(5)�ɑ�����Ă݂܂��B
����ƁA���R�̂��ƂȂ���A![]() �Ɛ����ɂȂ�܂���B
�Ɛ����ɂȂ�܂���B
�@�����ŁA��(5)�̕��q���݂āAd��������d��2�Ƃ��Ă݂܂��B
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�@2d��4�Ȃ̂ŁA4�̔{��a��48�����ɂ��A��(5)�ɑ�����Ă݂܂��B
����ƁAa��48�A![]() �Ac��73
�Ac��73
�@����d��6�Ƃ��Ă݂܂��B
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�@2d��12�Ȃ̂ŁA12�̔{��a��60�����ɂ��A��(5)�ɑ�����Ă݂܂��B
����ƁAa��60�A![]() �Ac��135
�Ac��135
�@���ɁAd��14�Ƃ��Ă݂܂��B
![]() ��a�̏����ɂȂ�܂��B
��a�̏����ɂȂ�܂��B
�@2d��28�Ȃ̂ŁA28�̔{��a��84�����ɂ��A��(5)�ɑ�����Ă݂܂��B
����ƁAa��84�A![]() �Ac��187
�Ac��187
��n���^����ꂽ�Ȃ�An��f�����������܂��B
�����Ď�(5)�̗l�q�����Ȃ���Ad�����߂Ă����A3��a�Ab�Ac����������悤�ł��B
��c��b�Ƃ̍��ōl���܂������Ab��a�Ƃ̍��ōl����ƁA�O���t���o�Ȑ��ɂȂ����Ȃ�܂��B
�uIga�v
�@�@�@�@�@�@ 01/19 00��02���@��M �X�V 2/8
��R�P�U��
�O���R2�{�S2�|�T2�A�P���S2�{�V2�|�W2�A�Q���T2�{�P�P2�|�P�Q2�A
�R���S2�{�U2�|�V2
�E�E�E�̂悤�ɂR���̕����̘a�ƍ��ŕ\�����Ƃ��ł��܂��B
�������A��2�{��2�|��2�@�́@��≨��≨���Ő������Ƃ���B
���P�F�S�C�T�C�U�C�V����2�{��2�|��2�i��≨��≨���Ő������j�̌`�ŕ\���Ă��������B
���Q�F��ʂɔC�ӂ̂O�ȏ�̐������@��2�{��2�|��2�i��≨��≨���Ő������j�̌`�ŕ\����邩�ۂ����l�@���������B�@
����ɂ��́A�h�����ł��B�v���Ԃ�̖K��ł����A��낵�����肢�������܂��B
���P�@
�@�S���T2�{�P�O2�|�P�P2���U2�{�V2�|�X2���V2�{�Q�Q2�|�Q�R2
�@�T���S2+�T2�|�U2�@�@�@�@�@�@�@�@�@ ���W2�{�Q�X2�|�R�O2
�U���T2�{�X2�|�P�O2�@�@�@�@�@�@�@ ���X2�{�R�V2�|�R�W2
�V���U2�{�P�S2�|�P�T2�@�@�@�@�@�@�@���P�O2�{�S�U2�|�S�V2
���Q
�@�@�ȉ��A�@��2�{��2�|��2�@���i���C���C���j�ƕ\���܂�
�O���i�R,�S,�T�j
�P���i�S,�V,�W�j
�Q���i�T�C�P�P�C�P�Q�j
����߂Ă�����A�����P�������Ă��āA���Ƃ��̍����P�Ȃ̂��C�ɂȂ��āA�R�������U�̂��̂������Ȃ����ƒT���Ă݂���A
�@�R���i�U,�P�U,�P�V�j
�������܂����B�܂��A���͂R�A�S�A�T�Ƒ����Ă��܂��̂ŁA�K�a�ŕ\�������ł��B
��������\�����A���A����
�@�������{�R�C�@�������i���{�Q�j�{�P�C�@�������i���{�Q�j�{�Q
�ƂȂ�܂��B�m���߂Ă݂�ƁA
�@�@�i���{�R�j2�{�i�i���{�R�j�i���{�Q�j�^�Q�{�P�j2�|�i�i���{�R�j�i���{�Q�j�^�Q�{�Q�j2
����2�{�U���{�X�{�i�i���{�R�j�i���{�Q�j�{�R�j�~�i�|�P�j
����2�{�U���{�X�|�i��2�{�T���{�X�j
����
�ƂȂ�A���͑傫���Ȃ�܂����A�C�ӂ̂O�ȏ�̐������@��2�{��2�|��2�i��≨��≨���Ő������j�̌`�ŕ\����邱�Ƃ��킩��܂����B���̃p�^�[���ŋ��߂����̂��A���P�̉E�[�̉ł��B
�����Ə��������ŕ\�����@�̃p�^�[����T�낤�ƁA�܂����ׂĂ݂܂����B
�O���i�R�C�S�C�T�j
�P���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�S�C�V�C�W�j
�Q���i�T�C�P�P�C�P�Q�j
�@�R���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�S�C�U�C�V�j�@���i�U�C�P�U�C�P�V�j
�@�S���i�T�C�P�O�C�P�P�j���i�V�C�Q�Q�C�Q�R�j
�@�T���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�S�C�T�C�U�j�@���i�U�C�P�T�C�P�U�j
�@�U���i�T�C�X�C�P�O�j���i�V�C�Q�P�C�Q�Q�j
�@�V���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�U�C�P�S�C�P�T�j
�@�W���i�T�C�W�C�X�j�@���i�V�C�Q�O�C�Q�P�j
�@�X���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�U�C�P�R�C�P�S�j
�P�O���i�T�C�V�C�W�j�@���i�V�C�P�X�C�Q�O�j
�P�P���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�U�C�P�Q�C�P�R�j
�P�Q���i�T�C�U�C�V�j�@���i�V�C�P�W�C�P�X�j
�P�R���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�U�C�P�P�C�P�Q�j
�P�S���@�@�@�@�@�@�@�@�@�i�V�C�P�V�C�P�W�j
��Ƌ����ł��ꂼ��̗���ɂȂ��Ă��āA���Ƃ����P�������Ă����A
�i�R�C�S�C�T�j�A�i�S�C�T�C�U�j�̂悤�ɁA�i���C���{�P�C���{�Q�j�̌`�ɂȂ�ƁA����ȏ�͌��点�Ȃ��̂ŁA�����Q���₵�Ď��̐��̃p�^�[���Ɉڍs����悤�ł��B���������݂��̂ł����A���܂������܂���ł����B
�܂��A�S���U2�{�V2�|�X2�̂悤�ɁA���Ƃ��̍����P�łȂ��p�^�[��������悤�ł��B
�Ƃ肠���������܂ł𑗂�܂��B
�u�O�p��K�v
01/24 00��02���@��M �X�V 2/8
�� ��316������O�p��K��
[���P]�@3������グ�܂����C���ɂ�����ł���邱�Ƃ��\�ł��B
�@
4��52�{102�|112 (c��b�{1)
�@ ��72�{222�|232 ( �V )
�@ ��112�{182�|212 (c��b�{3)
�@�@5��42�{52�|62 (c��b�{1)
�@�@ ��62�{152�|162 ( �V )
�@�@ ��72�{102�|122 (c��b�{2)
�@�@6��52�{92�|102 (c��b�{1)
�@�@ ��72�{212�|222 ( �V )
�@�@ ��92�{112�|142 (c��b�{3)
�@�@7��62�{142�|152 (c��b�{1)
�@�@ ��82�{282�|292 ( �V )
�@�@ ��102�{142�|172 (c��b�{3)
[���Q] ���ׂĂ̐���N (��0) �́C���R��a, b, c (a��b��c) ��p����
�@�@�@�@�@�@�@N��a2�{b2�|c2 �c�@
�ƕ\�����Ƃ��ł���B
�s�ؖ��t
c��b�{1�C���Ȃ킿�@N��a2�{b2�|(b�{1)2 �c�A �̌`�̏ꍇ���ؖ�����B
�A���C N��a2�|(2b�{1) �c�B
a��b ��� 0��N��a2�|2a�|1��(a�|1)2�|2
![]()
(1) a��� a��2k�{1 (k��1, 2, �c) �̂Ƃ�
�B���@N��(2k�{1)2�|(2b�{1)��2(2k2�{2k�|b)��0 �� b��2k(k�{1)
�@�@�܂� a��b ��� 2k�{2��b��, b��2k�{2 �̂Ƃ� N��4(k2�|1) ������
�@�@b��2k�{2��b��2k(k�{1) �͈̔͂̒l���Ƃ�Ƃ�, �B��N��0��N��4(k2�|1) �̂��ׂĂ̋����l���Ƃ�Bk �͂�����ł��傫���Ȃ�邩��C�B�́C�ǂ̂悤�ȋ����lN�����\�����Ƃ��ł���B
(2) a������ a��2k (k��1, 2, �c) �̂Ƃ�
�B���@N��(2k)2�|(2b�{1)��2(2k2�|b�|1/2)��0 �� b��2k2 �� b��2k2�|1
�@�@�܂� a��b ��� 2k�{1��b��, b��2k�{1 �̂Ƃ� N��4k2�|4k�|3������
�@�@b��2k�{1��b��2k2�|1 �͈̔͂̒l���Ƃ�Ƃ�, �B��N��1��N��4k2�|4k�|3 �̂��ׂĂ̊�l���Ƃ�Bk �͂�����ł��傫���Ȃ�邩��C�B�́C�ǂ̂悤�Ȋ�lN�����\�����Ƃ��ł���B
�@�@�ȏ�ŏؖ����ꂽ�B[��]
�u�E�B�E�v�@�@�@�@�@
01/27 20��18���@��M �X�V 2/8
�͂��߂܂��āA�E�B�E�Ɛ\���܂��B
���Ԃ�����܂����玟��ȍ~�����e�������܂��̂ŁA
��낵�����肢�������܂�
�i�P�j4=5^2+10^2�|11^2
5=4^2+5^2�|6^2
6=5^2+9^2�|10^2
�@�@�@7=6^2+14^2�|15^2
�i�Q�jC=B+1�Ƃ����B
�܂��AF(A,B)=A^2+B^2�|(B+1)^2�Ƃ����B
���������ƁAF(A,B)=A^2�|2B�|1�B
A��萔�ƌ���ƁA
B�̒l���P�������F�iA,B�j�̒l�́|�Q�������Ȃ鎖��������B
F(A,B)�͂O�ȏォ�����ł��邱�Ƃ�A��B����A
����A�ɂ��āAF�iA,B�j�̎�肤��l�͈̔͂��AA��p����ƁA
A����̎��A
0��F(A,B)��F(A,A+1)= A^2�|2A�|3�@�E�E�E�i�P�j
A�������̎��A
1��F�iA,B�j��F�iA,A+1�j��A^2�|2A�|3�@�E�E�E�i�Q�j
�ƕ\����B
F�iA,B�j�̎�肤��l�́A
�i�P�j���AA����̎��A
F�iA,B�j��0 ,2 ,�E�E�E, A^2�|2A�|3
�i�Q�j���AA�������̎��A
F�iA,B�j��1 ,3 ,�E�E�E,A^2�|2A�|�R
����l���^����ꂽ���ɁAA���\���傫�����鎖�ŁA
F�iA,B�j�͂��̒l����肤��B
����āA��ʂɔC�ӂ̂O�ȏ�̐����́@
A^2�{B^2�|C^2�i��≨��≨���Ő������j�̌`�ŕ\����B
�ЂƂ育�Ɓ@�i���T�C�g�l�̓��e���܂݂܂��̂ŁA�f�ڂ���ꍇ�͂����ӂ��������B�j
a^3+b^3-c^3�ɂ��čl���違���ׂĂ�����A
�C�ӂ̐��̗L���� r �ɑ��āAr = (a3 + b3)/(c3 + d3)�@�ƂȂ�悤�Ȑ��̐��� a�Cb�Cc�Cd �����݂���
����Ȃ̂��B�����B
���� ���u�L������\���������v�@�i�Q�O�P�T�N�P���Q�V���{���j
http://www004.upp.so-net.ne.jp/s_honma/mathbun/mathbun486.html
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
