平成２７年６月２１日

[流れ星]

　　　　　第321回数学的な応募解答

　　　　　　＜解答募集期間：5月31日〜6月21日＞

［整数の下三桁の数］

Ｎ＝２７^２０１５について次の数を求めよ。

（１）一の位の数

（２）十の位の数

（３）百の位の数

NO1「uchinyan」 05/31 12時18分　受信 更新 6/21

10 進法での下３桁を求めればいいので，mod 1000 の合同式で考えます。

N ≡ 27^2015 ≡ (3^3)^2015 ≡ 3^6045 ≡ (3^4)^1511 * 3 ≡ 81^1511 * 3

≡ (80 + 1)^1511 * 3 <----- 二項定理を適用して展開

≡ (1511C2 * 80^2 * 1^1509 + 1511C1 * 80^1 * 1^1510 + 1^1511) * 3

≡ (1511 * 755 * 6400 + 1511 * 80 + 1) * 3

≡ 881 * 3 ≡ 643

つまり，下３桁は 643 です。そこで，

(1) 3，(2) 4，(3) 6，

になります。

(感想)

この手の問題はそれなりによく見る問題で，

大体，フェルマーの小定理又はオイラーの定理か，二項定理の応用で解けます。

今回もオイラーの定理を使ってべき乗を減らしてもいいのですが，それだけではうまくいかず，

結局は二項定理のお世話になるようです。そこで最初から二項定理だけで押しました。

なお，合同式は記述を簡単にするために使っただけで本質的ではありません。

それと，個人的な感想としては，いくらでも計算のできるツールがある今の時代では，

定理の利用の練習や考え方としては重要でも，実際上はあまり意味がないかも知れませんね。

NO2「早起きのおじさん」 05/31 15時27分　受信 更新 6/21

の一の位の数値を知るには、 の一の位の数値を調べます。

そのため7のn乗の計算をして、様子をみます。

0乗	1乗	2乗	3乗	4乗
1	7	49	343	2401

この結果から一の位は、（1→7→9→3→･･･）の繰り返しになります。

4乗で一の位が1に戻るので、27の4n乗の計算をして様子をみます。

（下3桁のみ。千以上の位は*で省略します）

4乗	8乗	12乗	16乗	20乗
*441	*481	*121	*361	*201

20乗で十の位が（･･･0*）になるので、27の20n乗の計算をして様子をみます。

（下3桁のみ）

20乗	40乗	60乗	80乗	100乗
*201	*401	*601	*801	*001

100乗すると下3桁が、（･･･001）となります。

よって、

27×27×27＝19683

なので、

下3桁のみ調べていくと、

*001×*121×*683＝*643

なので、

（１）一の位は3

（２）十の位は4

（３）百の位は6

NO3「浜田明巳」 06/01 15時53分　受信 更新 6/21

VBSCRITの１行プログラムで計算する．

n=1:for j=1 to 2015:n=(n*27) mod 1000:next:msgbox n

　このプログラムにより，２７^２０１５の下３桁の数は６４３となる．
（１）１の位の数は３
（２）１０の位の数は４
（３）１００の位の数は６



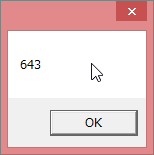
（別解）ｎ＝２７^２０１５とする．以下mod １０００で計算する．

　２７
×２７
―――
１８９
５４
―――
７２９　　　∴２７^２＝７２９≡−２７１

　２７１
×２７１
――――
　２７１
　９７
　２
――――
　４４１　　　∴２７^４＝(２７^２)^２≡(−２７１)^２≡４４１

　４４１
×４４１
――――
　４４１
　６４
　４
――――
　４８１　　　∴２７^８＝(２７^４)^２≡４４１^２≡４８１

　４８１
×４８１
――――
　４８１
　４８
　４
――――
　３６１　　　∴２７^１６＝(２７^８)^２≡４８１^２≡３６１

　３６１
×３６１
――――
　３６１
　６６
　３
――――
　３２１　　　∴２７^３２＝(２７^１６)^２≡３６１^２≡３２１

　３２１
×３２１
――――
　３２１
　４２
　３
――――
　　４１　　　∴２７^６４＝(２７^３２)^２≡３２１^２≡４１

　４１
×４１
―――
　４１
６４
―――
６８１　　　∴２７^１２８＝(２７^６４)^２≡４１^２≡６８１≡−３１９

　３１９
×３１９
――――
　８７１
　１９
　７
――――
　７６１　　　∴２７^２５６＝(２７^１２８)^２≡(−３１９)^２≡７６１≡−２３９

　２３９
×２３９
――――
　１５１
　１７
　８
――――
　１２１　　　∴２７^５１２＝(２７^２５６)^２≡(−２３９)^２≡１２１

　１２１
×１２１
――――
　１２１
　４２
　１
――――
　６４１　　　∴２７^１０２４＝(２７^５１２)^２≡１２１^２≡６４１≡−３５９

　３５９
×１２１
――――
　３５９
　１８
　９
――――
　４３９　　　∴２７^１５３６＝２７^１０２４・２７^５１２≡−３５９・１２１≡−４３９

　４３９
×２３９
――――
　９５１
　１７
　８
――――
　９２１　　　∴２７^１７９２＝２７^１５３６・２７^２５６≡(−４３９)・(−２３９)≡９２１≡−７９

　３１９
×　７９
――――
　８７１
　３３
――――
　２０１　　　∴２７^１９２０＝２７^１７９２・２７^１２８≡(−７９)・(−３１９)≡２０１

　２０１
×　４１
――――
　２０１
　　４
――――
　２４１　　　∴２７^１９８４＝２７^１９２０・２７^６４≡２０１・４１≡２４１

　３６１
×２４１
――――
　３６１
　４４
　２
――――
　　　１　　　∴２７^２０００＝２７^１９８４・２７^１６≡２４１・３６１≡１

　　∴２７^２００８＝２７^２０００・２７^８≡１・４８１＝４８１

　４８１
×４４１
――――
　４８１
　２４
　４
――――
　１２１　　　∴２７^２０１２＝２７^２００８・２７^４≡４８１・４４１≡１２１

　２７１
×１２１
――――
　２７１
　４２
　１
――――
　７９１　　　∴２７^２０１４＝２７^２０１２・２７^２≡１２１・(−２７１)≡−７９１≡２０９

　２０９
×　２７
――――
　４６３
　１８
――――
　６４３　　　∴ｎ＝２７^２０１５＝２７^２０１４・２７≡２０９・２７≡６４３

　故に一の位は３，十の位は４，百の位は６である．

NO4「ｽﾓｰｸﾏﾝ」 06/03 21時14分　受信 更新 6/21

今回はできましたと思います ^^

Ｎ＝２７^２０１５について次の数を求めよ。

（１）一の位の数

（２）十の位の数

（３）百の位の数

(1)

一の位は明らかに…7^2=49, 9^2=81 なので…

27^4 毎に1の位が1になる…

2015/4の余り=3

so…1*27^3≡3　mod 10

(2)

十の位は、たかだか100種類なので循環する…

1の桁が27^4毎に循環するので、その場合で考える…(高々９回の計算でわかる)

27^4=41

41^2=81

41^3=21

41^4=61

41^5=01

つまり…

(27^4)^5≡1

2015/20の余り=15・・・15=8+4+2+1

so…81*41*27^2*27=21*83=43

つまり…

27^2015≡4　mod 100

(3)

百の位でもたかだか1000種類しかないので循環するから、

10の桁で循環するのが (27^4)^5 なので、その場合で考える…(やはり、高々9回の計算でわかる)

27^4=441

441^4=361

361*441=201

つまり…

(27^4)^5≡201

201^2=401

201^3=601

201^4=801

201^5=001

つまり…

(27^20)^5≡1　mod 1000

so…

2015/100の余り=15・・・15=8+4+2+1

so…

441^2*441*27^2*27=121*683=643

ですね ^^

NO5「二度漬け白菜」 06/16 21時28分　受信 更新 6/21

(答)
(1) 一の位の数は 3
(2) 十の位の数は 4
(3) 百の位の数は 6

27^2015≡643(mod 1000) であることが次のようにして
示せます．

27^2015=3^6045.
3^5=243.
3^10≡243^2≡59049≡49(mod 1000).
3^20≡49^2≡2401≡401(mod 1000).
3^40≡401^2≡160801≡801(mod 1000).
3^80≡801^2≡641601≡601(mod 1000).
3^100≡401*601≡241001≡1(mod 1000).
3^6045≡((3^100)^60)*(3^40)*(3^5)≡(1^60)*(801)*(243)≡194643≡643(mod 1000).

オイラーの定理から3^400≡1(mod 1000)
であることがいえるので，3^6000≡(3^400)^15≡1(mod 1000)
とすることもできます．
ですが，なにかもう少し気の利いた解法があるような気がします．

NO6「にいばりZ12」 06/20 04時29分　受信 更新 6/21

27を20と7に分解し2項展開します

27²⁰¹⁵

=(20+7) ²⁰¹⁵

=₂₀₁₅C₀7²⁰¹⁵・20⁰

+₂₀₁₅C₁7²⁰¹⁴・20¹

+₂₀₁₅C₂7²⁰¹³・20²

+₂₀₁₅C₃7²⁰¹²・20³

・

・

・

+₂₀₁₅C₂₀₁₃7²・20²⁰¹³

+₂₀₁₅C₂₀₁₄7¹・20²⁰¹⁴

+₂₀₁₅C₂₀₁₅7⁰・20²⁰¹⁵

=　　　7²⁰¹⁵

+40300・7²⁰¹⁴

+2015・2014/2・7²⁰¹³・20²

・

・

・

+₂₀₁₅C₂₀₁₃7²・20²⁰¹³

+₂₀₁₅C₂₀₁₄7¹・20²⁰¹⁴

+₂₀₁₅C₂₀₁₅7⁰・20²⁰¹⁵

3項以降の下3桁はいずれも0です

従って

7²⁰¹⁵+40300・7²⁰¹⁴・・・�@

の下3桁を調べればいいことになります

ここで7⁴=2401

なので上記1項目は

7²⁰¹⁵=(2400+1) ⁵⁰³・7³

となり2項展開すると

(2400+1) ⁵⁰³=₅₀₃C₀1⁵⁰³・2400⁰+₅₀₃C₁1⁵⁰²・2400¹+・・・

で3項目以降が下3桁0

�@の下3桁を調べるには

(1+503・2400) ・7³+40300・(1+503・2400)・7²

の下3桁を調べればよくさらにこれは

(1+3・400) ・7³+300・7²

を計算すればよいことになります

この下3桁は643となります・・・・・・・・・・・・・回答

NO6「にいばりZ12」 06/21 01時27分　受信 更新 6/21

にいばりZ12です

試行錯誤しながら

もう少しだけ簡単な方法で解いてみました

27=3³、3⁴=81から

27²⁰¹⁵=3 ⁶⁰⁴⁵=3・81 ¹⁵¹¹=3・(1+80) ¹⁵¹¹

ここで

(1+80) ¹⁵¹¹

=₁₅₁₁C₀1¹⁵¹¹・80⁰

+₁₅₁₁C₁1¹⁵¹⁰・80¹

+₁₅₁₁C₂1¹⁵⁰⁹・80²

+₁₅₁₁C₃1¹⁵⁰⁸・80³

・

・

・

+₂₀₁₅C₂₀₁₃1²・80²⁰¹³

+₂₀₁₅C₂₀₁₄1¹・80²⁰¹⁴

+₂₀₁₅C₂₀₁₅1⁰・80²⁰¹⁵

=　　　1¹⁵¹¹

+1510・1¹⁵¹⁰・80¹

+1511・1510/2・1¹⁵⁰⁹・80²・

・

・

+₂₀₁₅C₂₀₁₃7²・20²⁰¹³

+₂₀₁₅C₂₀₁₄7¹・20²⁰¹⁴

+₂₀₁₅C₂₀₁₅7⁰・20²⁰¹⁵

3項以降の下3桁はいずれも0です

従って

3・(1¹⁵¹¹+1511・1¹⁵¹⁰・80¹)・・�@

の下3桁を調べればいいことになりますがこれは

3・(1+11・80)

の下3桁を調べればよく計算すると

3・881=2643

なので下3桁は643となります・・・・・・・・・・・・・回答

合同式や、フェルマーの小定理で考えましたが行き着けず結局何か一番泥臭い解き方となってしまいました

結論的には

27²⁰¹⁵≡643　（mod1000）

となるのでしょうが皆さんの回答を拝見するのが楽しみです。

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。