平成２７年１月１７日

[流れ星]

　　　　　第329回数学的な応募解答

　　　　　　＜解答募集期間：1２月20日〜1月17日＞

［通過領域＋α］

　皆さん、過去の大学入試問題を見ていると、「関数のグラフが通過する範囲を図示せよ」という問題を見かけます。

最近では今年東大で出題されていました。そこで、次の問題を考えました。

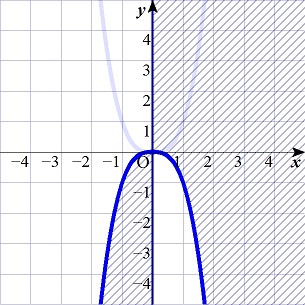
問題１：１次関数ｙ＝２ｔｘ−ｔ^２がｔ≧０の範囲で変化するとき、この１次関数のグラフが通過する範囲を求め、図示せよ。

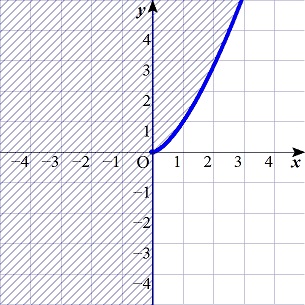
問題２：２次関数ｙ＝ｔｘ^２＋（１/４ｔ）ｘ　がｔ>０の範囲で変化するとき、この２次関数のグラフが通過する範囲を求め、図示せよ。

問題３：３次関数ｙ＝ｘ^３−４ｔｘ^２＋２ｔ^２ｘ　がｔ≧０の範囲で変化するとき、この３次関数のグラフが通過する範囲を求め、図示せよ。

新年あけましておめでとうございます。平成２８年もご愛顧賜りますようお願い申し上げます。

問題４：「数学Ａ」という教科書に整数の性質という章があります。（ここでは、約数は正の自然数としておきます。）

例えば、８＝２^３と素因数分解できますから、正の約数は、１，２，４，８です。

だから、８の約数の個数は　３＋１＝４　　（個）

　また、８と互いの素な数は、１，３，５，７の４個です。

これは大変興味深い結果です。正の約数の個数と互いに素な数の個数が一致しています。

　勿論、自然数Ｎについて、Ｎ＝ａ^ｐ×ｂ^ｑ×ｃ^ｒ×・・・と素因数分解できたとき、

Ｎの約数の個数は、　(ｐ＋１)(ｑ＋１)(ｒ＋１)・・・　で求まります。

Ｎ以下で、Ｎと互いに素の数の個数は、オイラー関数φ（Ｎ）で表すと、

φ（Ｎ）＝Ｎ(1−１/ａ)(1−１/ｂ)(1−１/ｃ) ・・・で書けます。

ここで、問題です。自明な１は除いてもいいでしょう。

「自然数Ｎについて、Ｎの正の約数の個数と、Ｎ以下でＮと互いに素な数の個数とが一致するような自然数Ｎは一体どんな数でしょう。」

ＮＯ１「uchinyan」 12/20 17時19分　受信 更新

領域の図示はテキストではできないので，可能な限り，式と言葉で表現することにします。

問題１：

y = 2tx - t^2，t >= 0

t^2 - 2xt + y = 0

これを t の２次方程式と見れば，t >= 0 で解をもつことが必要十分条件です。

f(t) = t^2 - 2xt + y = (t - x)^2 + y - x^2 として f(t) のグラフを考えれば，

x >= 0 の場合，y - x^2 <= 0，y <= x^2，

x < 0 の場合，f(0) <= 0，y <= 0，

結局，

x < 0 の場合：y <= 0，x >= 0 の場合：y <= x^2，

になります。

問題２：

y = tx^2 + (1/(4t))x，t > 0

(4x^2)t^2 - (4y)t + x = 0

これを t の方程式と見れば，t > 0 で解をもつことが必要十分条件です。

x = 0 の場合，y = 0，

x ≠ 0 の場合，

f(t) = (4x^2)t^2 - (4y)t + x = (4x^2)(t - y/(2x^2))^2 + (x^3 - y^2)/x^2 として f(t) のグラフを考えれば，

y/(2x^2) > 0 のとき，(x^3 - y^2)/x^2 <= 0，y^2 >= x^3，x < 0 又は y >= √(x^3)，

つまり，y > 0 かつ y >= √(x^3)，

y/(2x^2) <= 0 のとき，f(0) < 0，x < 0，

つまり，y <= 0 かつ x < 0，

結局，

x < 0 の場合：すべて，x = 0 の場合：y = 0，x > 0 の場合：y >= √(x^3)，

なります。

問題３：

y = x^3 - (4t)x^2 + (2t^2)x，t >= 0

(2x)t^2 - (4x^2)t + (x^3 - y) = 0

これを t の方程式と見れば，t > 0 で解をもつことが必要十分条件です。

x = 0 の場合，y = 0，

x ≠ 0 の場合，

f(t) = (2x)t^2 - (4x^2)t + (x^3 - y) = (2x)(t - x)^2 - (x^3 + y) として f(t) のグラフを考えれば，

x > 0 のとき，- (x^3 + y) <= 0，y >= - x^3，

x < 0 のとき，f(0) >= 0，y <= x^3，

結局，

x < 0 の場合：y <= x^3，x = 0 の場合：y = 0，x > 0 の場合：y >= - x^3，

なります。

(ちょっとだけ考察)

領域図示の問題は境界の辺りが微妙でそれには役立ちませんが，概要は次のようにしても分かるでしょう。

問題１：

この１次関数は，y = x^2 の (t,t^2) における接線の式です。

このことから結果は容易に予想できます。

問題２：

x = 0 の場合は明らか。

x > 0 の場合は，相加相乗平均から，

y = tx^2 + (1/(4t))x >= 2√(tx^2 * (1/(4t))x) = √(x^3)，

です。

x < 0 の場合は，x -> -x と置き換えれば，y = tx^2 - (1/(4t))x，ですが，

x に関係なく，t -> +0 で y -> -∞，t -> ∞ で y -> ∞，途中は連続的に変化します。

このことから結果は容易に予想できます。

問題３：

y = x^3 - (4t)x^2 + (2t^2)x は，x = 0，(2 ± √2)t，で x 軸と交わります。

このことと３次関数の増減や曲がり具合の様子から，ある程度は結果を予想できます。

正確ではないとしても，論理的に裏打ちされたある程度の予想があれば，助けにはなるでしょう。

(ちょっとだけ考察　終わり)

問題４：

a，b，c，… は素数，p，q，r，… は 0 以上の整数，ただし 1 は除くので少なくとも１つは 0 でない，として，

与えられているように，N = a^p * b^q * c^r * …，のとき，

n(N) = N の約数の個数 = (p + 1)(q + 1)(r + 1)…，

φ(N) = N(1 - 1/a)(1 - 1/b)(1 - 1/c)… ，

です。これはそのまま使います。

さて，φ(N) = n(N) となる N を求めるのですが，

φ(N)/n(N) = φ(a^p)/n(a^p) * φ(b^q)/n(b^q) * φ(c^r)/n(c^r) * … = 1，

として，φ(N)/n(N) = 1 となる N を探すことにします。

まず，x を x >= 2 の実数として，

f(x) = φ(x^p)/n(x^p) = (x^p * (1 - 1/x))/(p + 1) = (x^p - x^(p-1))/(p + 1)，

を考えると，

f'(x) = (px^(p-1) - (p-1)x^(p-2))/(p + 1) = (px^(p-2) * (x - (p-1)/p)/(p + 1)，

x >= 2 なので，f'(x) > 0，f(x) は x >= 2 で狭義に単調増加です。

したがって，φ(x^p)/n(x^p) は x = 2 が最小です。

次に，x を x >= 1 の実数として，

g(x) = φ(a^x)/n(a^x) = (a^x * (1 - 1/a))/(x + 1) = (a - 1) * a^(x-1)/(x + 1)，

を考えると，log を底が e の自然対数として，

g'(x) = (a - 1) * (log(a) * a^(x-1) * (x + 1) - a^(x-1) * 1)/(x + 1)^2

= (a - 1) * a^(x-1) * (log(a) * (x + 1) - 1)/(x + 1)^2，

ここで，2^2 = 4 > e > 2，a >= 2 > e^(1/2)，log(a) >= log(2) > 1/2，で，x >= 1 なので，

g'(x) の分子 = (a - 1) * a^(x-1) * (log(a) * (x + 1) - 1) > 1 * 1 * (1/2 * (1 + 1) - 1) = 0，

そこで，g'(x) > 0，g(x) は x >= 1 で狭義に単調増加です。

したがって，φ(a^x)/n(a^x) は x = 1 が最小です。

一般の N は幾つかの素因数のべき乗の積になるので，今調べた結果を掛け合わせたものになります。

これらのことと，

φ(2^1)/n(2^1) = 1/2，φ(2^2)/n(2^2) = 2/3，φ(2^3)/n(2^3) = 4/4 = 1，φ(3^1)/n(3^1) = 2/2 = 1，

より，φ(N)/n(N) = 1 となる N のうち，

N の素因数が 3 以上だけの場合は，N = 3^1 = 3，だけが解で，それ以外は φ(N) > n(N)，

と分かります。

一方で，2^3 = 8 が解なので，

N の素因数に 2 が含まれる場合は，2^p，p >= 4，では，φ(N) > n(N)，です。

つまり，3，8 以外に可能性があるのは，自明な 1 を除くと，

2^1 = 2，2^2 = 4，2^3 = 8，と 2 以外の素因数の組み合わせだけです。

そこで，N の 2 以外の素因数のべき乗の積を M とします。すると，

φ(N)/n(N) = (φ(2^p)φ(M)))/(n(2^p)n(M)) = 1，φ(M)/n(M) = n(2^p)/φ(2^p)，

これに，上記の狭義の単調増加性を絡めて，N を探します。

ただし，φ(3^1)/n(3^1) = 1 なので，

N に 3 の素因数のべき乗が含まれない場合は，N が解ならば 3N も解になることに注意です。

2 の素因数のべき乗が 2^1 = 2 の場合

φ(2^1)/n(2^1) = 1/2，なので，φ(M)/n(M) = 2，です。

φ(3^1)/n(3^1) = 2/2 = 1，より，これとの積は解ではありません。

φ(3^2)/n(3^2) = 6/3 = 2，より，2 * 3^2 = 18，は解です。

φ(5^1)/n(5^1) = 4/2 = 2，より，2 * 5 = 10，は解です。また，先の注意より 30 も解です。

φ(7^1)/n(7^1) = 6/2 = 3，より，これとの積は解ではありません。

そして，狭義の単調増加性より，他に解はありません。

2 の素因数のべき乗が 2^2 = 4 の場合

φ(2^2)/n(2^2) = 2/3，なので，φ(M)/n(M) = 3/2，です。

φ(3^1)/n(3^1) = 2/2 = 1，より，これとの積は解ではありません。

φ(3^2)/n(3^2) = 6/3 = 2，より，これとの積は解ではありません。

φ(5^1)/n(5^1) = 4/2 = 2，より，これとの積は解ではありません。

そして，狭義の単調増加性より，他に解はありません。

2 の素因数のべき乗が 4 = 2^3 の場合

φ(2^3)/n(2^3) = 4/4 = 1，なので，φ(M)/n(M) = 1，です。

φ(3^1)/n(3^1) = 2/2 = 1，より，8 * 3^1 = 24，は解です。

φ(3^2)/n(3^2) = 6/3 = 2，より，これとの積は解ではありません。

そして，狭義の単調増加性より，他に解はありません。

以上より，自明な 1 以外の解は，

3，8，10，18，24，30，

になります。

(感想)

問題１：〜問題３；の領域の図示は，テキストでは図が描けないので，式と言葉でご勘弁を。

この手の問題は境界などでうっかりミスがあり得るので，大丈夫か少し心配です。

問題４：は，最初，はてどうするか，と思ったのですが，ひとまず上限を考えよう，と思ったらうまくいきました。

論理的に問題はないと思いますが，説明が少し分かりづらいかな，と心配。

2015年ももう少し。早いものです。2016年も宜しくお願い致します。

ＮＯ２「浜田明巳」 12/22 10時19分　受信 更新 1/17

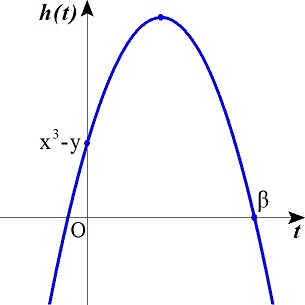
問題１
　ｙ＝２ｔｘ−ｔ^２（ｔ≧０）より，
　　ｔ^２−２ｘｔ＋ｙ＝０
　ｆ(ｔ)＝ｔ^２−２ｘｔ＋ｙとする．
　ｔの２次方程式ｆ(ｔ)＝０がｔ≧０の範囲で解を持てばよい，
　　ｆ(ｔ)＝(ｔ^２−２ｘｔ＋ｘ^２−ｘ^２)＋ｙ＝(ｔ−ｘ)^２＋(ｙ−ｘ^２)
であり，ｆ(ｔ)のグラフは，下に凸の放物線であるから，グラフから，
i). ｘ≧０，ｆ(ｘ)＝ｙ−ｘ^２≦０，ｆ(０)＝ｙ≧０のとき，条件を満たす．
　このとき，ｘ≧０，ｙ≦ｘ^２，ｙ≧０

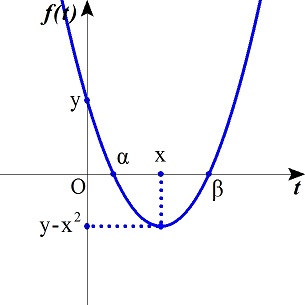
ii). ｆ(０)＝ｙ≦０のとき，条件を満たす．

　i)，ii)より，求める領域は図の斜線部分である，ただし境界線を含む，


問題２
　ｙ＝ｔｘ^２＋１／４・ｔｘ（ｔ＞０）より，
　　(ｘ^２＋１／４・ｘ)ｔ−ｙ＝０
　ｇ(ｔ)＝(ｘ^２＋１／４・ｘ)ｔ−ｙとする．
　ｔの方程式ｇ(ｔ)＝０がｔ＞０の範囲で解を持てばよい．グラフから，
i). ｘ^２＋１／４・ｘ＞０，ｇ(０)＝−ｙ＜０のとき，条件を満たす．
　このとき，ｘ(ｘ＋１／４)＞０から，ｘ＜−１／４または０＜ｘであり，ｙ＞０

ii). ｘ^２＋１／４・ｘ＜０，ｇ(０)＝−ｙ＞０のとき，条件を満たす．
　このとき，−１／４＜ｘ＜０，ｙ＜０

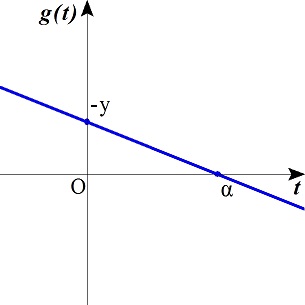
iii). ｘ^２＋１／４・ｘ＝−ｙ＝０のとき，条件を満たす．
　このとき，ｘ＝０またはｘ＝−１／４，ｙ＝０

　i)〜iii)より，求める領域は，図の斜線部分である．境界線のｘ軸，ｙ軸，直線ｘ＝−１／４上の点は除くが，点(０，０)，(−１／４，０)を含む．


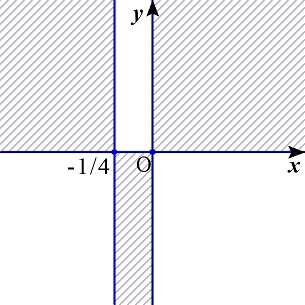
問題３
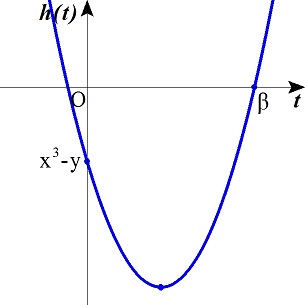
　ｙ＝ｘ^３−４ｔｘ^２＋２ｔ^２ｘ（ｔ≧０）より，
　　２ｘｔ^２−４ｘ^２ｔ＋(ｘ^３−ｙ)＝０
　ｈ(ｔ)＝２ｘｔ^２−４ｘ^２ｔ＋(ｘ^３−ｙ)とする．
　ｔの方程式ｈ(ｔ)＝０がｔ≧０の範囲で解を持てばよい．
　　ｈ(ｔ)＝２ｘ(ｔ^２−２ｘｔ＋ｘ^２−ｘ^２)＋(ｘ^３−ｙ)＝２ｘ(ｔ−ｘ)^２＋(−ｘ^３−ｙ)
であるから，
i). ２ｘ＞０，ｘ≧０，h(ｘ)＝−ｘ^３−ｙ≦０，ｈ(０)＝ｘ^３−ｙ≧０のとき，条件を満たす．
　このとき，ｘ＞０，−ｘ^３≦ｙ≦ｘ^３

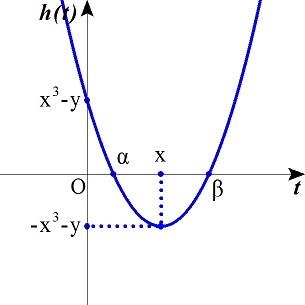
ii). ２ｘ＜０，ｘ≧０，ｈ(ｘ)＝−ｘ^３−ｙ≧０，ｈ(０)＝ｘ^３−ｙ≦０のとき，条件を満たすが，このようなｘは存在しない．

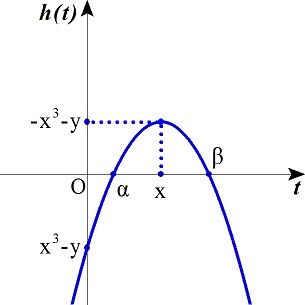
iii). ２ｘ＞０，ｈ(０)＝ｘ^３−ｙ≦０のとき，条件を満たす．
　このとき，ｘ＞０，ｙ≧ｘ^３

iv). ２ｘ＜０，ｈ(０)＝ｘ^３−ｙ≧０のとき，条件を満たす．
　このとき，ｘ＜０，ｙ≦ｘ^３

v). ２ｘ＝−４ｘ^２＝ｘ^３−ｙ＝０のとき，条件を満たす．
　このとき，ｘ＝ｙ＝０

　i)〜v)から，求める領域は図の斜線部分である．境界線の曲線ｙ＝ｘ^３（ｘ＜０），ｙ＝−ｘ^３（ｘ＞０）上の点は含み，ｙ軸上の点は除く．また原点を含む．


問題４
　ＶＢＳＣＲＩＰＴで解いた，Ｎの最大値を５０００としたときの解は，以下の６個の自然数であると分かる．
　　３，８，１０，１８，２４，３０
　Ｎをもっと大きくした場合でも，解はこれらの６個であろう，

max=5000
kotae="Ｎの最大値="&max&chr(13)
kosuu=0
for N=2 to max
  k1=0
  for j=1 to N
   k1=k1-(N mod j=0)
  next
  k2=0
  for j=1 to N
   k2=k2-(GCM(N,j)=1)
  next
  if k1=k2 then
   kosuu=kosuu+1
   if kosuu>1 then
    kotae=kotae&","
   end if
   kotae=kotae&N
  end if
next
msgbox kotae
'
function GCM(a,b)
  if b>0 then
   GCM=GCM(b,a mod b)
  else
   GCM=a
  end if
end function

（最後に）
　問題の条件でＮ≧２とするのは，当然といえば当然であるが，ここでささいな疑問がわきました，
　Ｎ＝１として，上記のプログラムを走らせた場合，１を解と表示します，
　しかしＮ＝１のとき，１とＮは互いに素でしょうか？　確かに２数（？）の最大公約数は１ですが，その２数が等しい場合も互いに素であるといえるのでしょうか？ 　Ｎ＝１はそんなに自明でしょうか？

「浜田明巳」 12/22 10時53分　受信 更新 1/17

（別解）グラフを使わない解法（個人的にはこちらの方が好きです）
問題１
　ｆ(ｔ)＝ｔ^２−２ｘｔ＋ｙとして，ｔの２次方程式ｆ(ｔ)＝０がｔ≧０の範囲で解を持てばよい，
　２解をα，βとする．α，βは実数なので，判別式をＤとすると，
　　Ｄ／４＝ｘ^２−ｙ≧０
　　∴ｙ≦ｘ^２
　解と係数の関係から，α＋β＝２ｘ，αβ＝ｙ
i). α≧０，β≧０のとき，
　　α＋β≧０，αβ≧０
　　∴２ｘ≧０，ｙ≧０
　　∴ｘ≧０，ｙ≧０
ii). α＞０かつβ＜０，またはα＜０かつβ＞０，またはα＝０，またはβ＝０のとき，
　　αβ≦０
　　∴ｙ≦０
　i)，ii).をまとめると，・・・

問題２
　ｇ(ｔ)＝(ｘ^２＋１／４・ｘ)ｔ−ｙとする．
　ｔの方程式ｇ(ｔ)＝０がｔ＞０の範囲で解を持てばよい．
i). ｘ^２＋１／４・ｘ≠０のとき，ｘ≠０かつｘ≠−１／４であり，
　　ｙ／(ｘ^２＋１／４・ｘ)＞０
　　∴ｘ(ｘ＋１／４)・ｙ＞０
　　∴{(ｘ＜−１／４または０＜ｘ)かつｙ＞０}または(−１／４＜ｘ＜０かつｙ＜０)
ii). ｘ^２＋１／４・ｘ＝−ｙ＝０のとき，
　　(ｘ，ｙ)＝(０，０)，(−１／４，０)
　i)，ii)をまとめると，・・・

問題３
　ｈ(ｔ)＝２ｘｔ^２−４ｘ^２ｔ＋(ｘ^３−ｙ)とする．
　ｔの方程式ｈ(ｔ)＝０がｔ≧０の範囲で解を持てばよい．
i). ２ｘ≠０のとき，ｘ≠０である．
　２解をα，βとする．α，βは実数なので，判別式をＤとすると，
　　Ｄ／４＝４ｘ^４−２ｘ(ｘ^３−ｙ)＝２ｘ(ｘ^３＋ｙ)≧０
　　∴(ｘ≧０かつｙ≧−ｘ^３)または(ｘ≦０かつｙ≦−ｘ^３)
　ｘ≠０から，
　　(ｘ＞０かつｙ≧−ｘ^３)または(ｘ＜０かつｙ≦−ｘ^３)
　解と係数の関係から，α＋β＝２ｘ，αβ＝(ｘ^３−ｙ)／(２ｘ)
　ア). α≧０，β≧０のとき，
　　α＋β≧０，αβ≧０
　　∴２ｘ≧０，(ｘ^３−ｙ)／(２ｘ)≧０
　　∴ｘ＞０，ｙ≦ｘ^３
　イ). α＞０かつβ＜０，またはα＜０かつβ＞０，またはα＝０，またはβ＝０のとき，
　　αβ≦０
　　∴(ｘ^３−ｙ)／(２ｘ)≦０
　　∴(ｘ＞０かつｙ≧ｘ^３)または(ｘ＜０かつｙ≦ｘ^３)
ii). ２ｘ＝０のとき，ｘ＝ｙ＝０
　i)，ii).をまとめると，・・・

（蛇足）
　問題１，３ではｔ≧０であり，問題２ではｔ＞０となっているので，気がつきました．
　問題２の
　　(１／４ｔ)ｘ
を，
　　{１／(４ｔ)}ｘ
と解釈すると，次の解答となる．
　ｙ＝ｔｘ^２＋{１／(４ｔ)}ｘから，
　　ｘ^２ｔ^２−ｙｔ＋１／４・ｘ＝０
　ｇ(ｔ)＝ｘ^２ｔ^２−ｙｔ＋１／４・ｘとする．
　ｘの方程式ｇ(ｔ)＝０が，ｔ＞０の範囲で解を持てばよい．
i). ｘ≠０のとき，判別式をＤとすると，
　　Ｄ＝ｙ^２−ｘ^３≧０
　　∴ｙ^２≧ｘ^３
　２解をα，βとする．
　解と係数の関係から，α＋β＝ｙ／ｘ^２，αβ＝１／(４ｘ)
　ア). α＞０，β＞０のとき，α＋β＞０，αβ＞０
　　∴ｙ／ｘ^２＞０，１／(４ｘ)＞０
　　∴ｘ＞０，ｙ＞０
　イ). α＞０，β＜０，またはα＜０，β＞０のとき，
　　αβ＜０
　　∴１／(４ｘ)＜０
　　∴ｘ＜０
ii). ｘ＝０のとき，ｇ(ｔ)＝−ｙｔ＝０
　故に−ｙ＝０，すなわち(ｘ，ｙ)＝(０，０)となる．
　i)，ii)から，求める領域は図の斜線部分である．ただし，曲線ｙ＝ｘ^３／２（ｘ＞０）上の点は含み，ｙ軸（ｘ≠０）上の点は除く．また原点を含む．

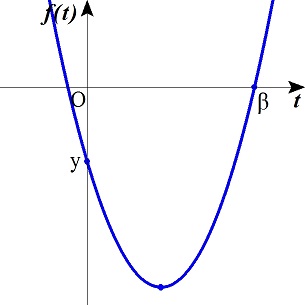
ＮＯ３「早起きのおじさん」 12/25 14時42分　受信 更新 1/17

問題1

tの２次方程式の判別式を調べて、

よって、 が必要条件です。

さて、曲線 の上の点 における接線は、 より、 です。

下の図の接点のｘ座標がtです。

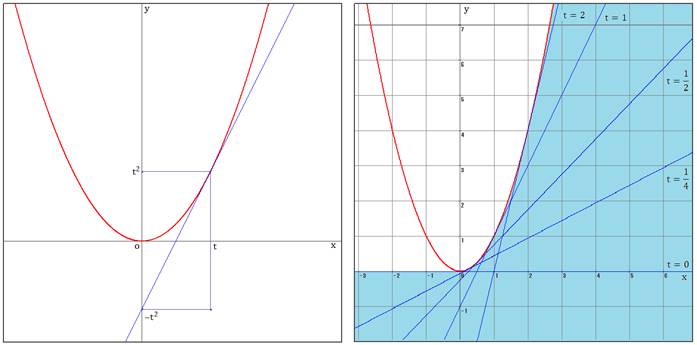
t≧0なので、右の図の青く塗った部分が求める範囲です。

問題2

tの２次方程式の判別式を調べて、

よって、が必要条件です。

（曲線 が境界線になります）

さて、上の曲線の式から、このグラフは、 でｘ軸と交わります。

また、 とすると、

より

つまり、グラフは境界線と で接します。

なので、グラフはｘが大きくなると境界線から離れていきます。

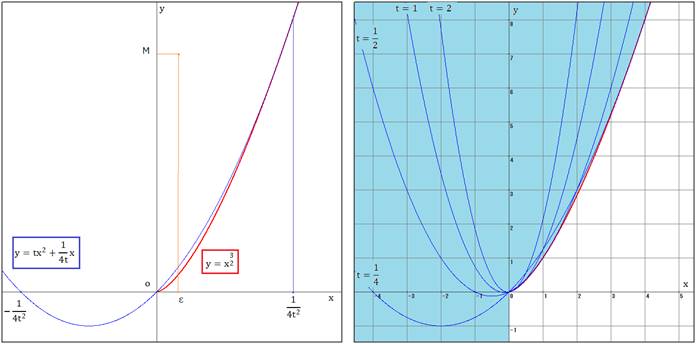
右の図の青く塗った部分が求める範囲です。

念のためｙ軸の近くをグラフが通るかみておきます。

εは正でごく小さな値、Mはとても大きな値とします。

ｘ＝ε、ｙ＝Mをｔの２次方程式に代入すると、

つまり、とても大きな数かとても小さな正の数のときです。

ついでに、ｘ＝−ε、ｙ＝−Mをｔの２次方程式に代入すると、

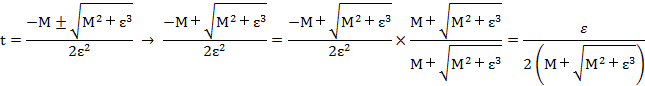
つまり、tがとても小さな正の数のとき、グラフが左下でｙ軸のそばを通ります。

ただし、原点以外のｙ軸は除きます。

問題3

tの２次方程式の判別式を調べて、

曲線 が境界線になります。

さて、上の曲線の式から、このグラフは、 でｘ軸と交わります。

また、

とすると、

つまり、グラフは境界線と で交わり、 で接します。

また、式の形から のとき、 です。

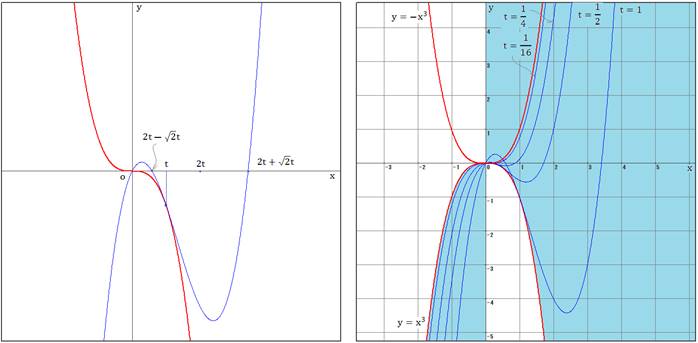
右の図の青く塗った部分が求める範囲です。

また、ｘ＝ε、ｙ＝Mをｔの２次方程式に代入すると、

つまり、とても大きなtのときに、ｙ軸のそばをグラフが通ります。

これも原点以外のｙ軸は除きます。

問題4

以下a、b、c、・・・を素数とします。

●Nが素数のときを調べます。

N=aの約数は、2個です。

a以下でaと互いに素な数は、 個です。

ゆえに、N＝a＝3です。

3より大きな素数の約数の個数は2ですが、互いに素な数の個数が2より大きくなります。

● のときを調べます。

Nの約数は、p＋1個です。

N以下でNと互いに素な数は、 個です。

問題の例にあったように、 のときは、 となります。

aが2より大きくなると、互いに素な数の個数が４より大きくなります。

のときを調べます。

・ のとき、約数は4個、互いに素な数は 個です。

　aとbは異なるので、a＝2、b＝5つまり、N＝10 となります。

　

・ のとき、約数は6個、互いに素な数は 個です。

　aとbは異なるので、a＝2、b＝3つまり、N＝18 となります。

・ のとき、約数は8個、互いに素な数は 個です。

　aとbは異なるので、a＝3、b＝2つまり、N＝24 となります。

・ のとき、約数は10個、互いに素な数は 個です。

この場合、互いに素な数の個数は最低が、a＝3、b＝2のときの、 です。

　それ以外は、a＝2、b＝3のときの、 個より多くなります。

・ のとき、約数は9個、互いに素な数は 個です。

この場合、互いに素な数の個数は最低は、a＝2、b＝3のときの、 です。

a、bの指数がともに2以上になると、該当する数はありません。

・ のとき、約数は8個、互いに素な数は 個です。

　a、b、cは異なるので、a＝2、b＝3、c＝5つまり、N＝30 となります。

・ のとき、約数は12個、互いに素な数は 個です。

この場合、互いに素な数の個数は最低は、a＝2、b＝3、c＝5のときの、16です。

a、b、cの指数がどれか2以上になると、該当する数はありません。

・ のとき、約数は16個、互いに素な数は 個です。

この場合、互いに素な数の個数は最低は、a＝2、b＝3、c＝5、d＝7のときの、48です。

該当する数はありません。

●以上から、3、8、10、18、24、30が該当します。

ＮＯ４「スモークマン」 12/31 23時32分　受信 更新 1/17

問題

「自然数Ｎについて、Ｎの正の約数の個数と、Ｎ以下でＮと互いに素な数の個数とが一致するような自然数Ｎは一体どんな数でしょう。」

回答

N=1 の自明以外のもので…

素因数が1個のとき

(1) N=p^a

a+1=p^(a-1)*(p-1)

右辺は、pが2以外の奇素数でも偶数…

aは奇数

a=3のとき、4=2*p^2も成り立たず、それ以上の奇数でも、

左辺は加法的で右辺は累乗的で右辺の方が大きくなる(アバウトですが)

so…あるとしたら…

a=1

2=p-1・・・p=3・・・N=3

p=2 のとき

a+1=2^(a-1)

a=3・・・N=2^3

(2) N=p*q

4=(p-1)(q-1)

p-1=1, q-1=4・・・N=2*5=10

(3) N=p*q*r

8=1*2*4 しかない…

N=2*3*5=30

(4) N=p*q*r*s

16=1*2*4*2 でダメ…2^k=2^(n(n+1)/2)

2k=n(n+1)・・・2*1 or 2*3 しかない…ので素因数の数が4個以上ではなし

(5) N=p^a*q^b

(a+1)(b+1)=p^(a-1)*(p-1)*q^(b-1)*(q-1)

・ a=2のとき、

3(b+1)=p*q^(b-1)*(q-1)

p=3

b+1=q^(b-1)*(q-1)

b=1,q=2・・・N=3^2*2=18

・a=3 のとき、

4(b+1)=p^2*(p-1)*q^(b-1)*(q-1)

：p=2

b+1=q^(b-1)*(q-1)

b=1・・・2=q-1・・・q=3・・・N=2^3*3=24

a>=4 のときは、両辺の大小を考えたら無理だと思うんだけど、

どう言えばいいのかわからない…

以上ですべてだと思えるので…

1, 3, 8, 10, 18, 24, 30

ＮＯ５「二度漬け白菜」 01/06 22時19分　受信 更新 1/17

問題2の問題文中の式 y=t*x^2+(1/4t)*x についてですが，
この式を y=t*x^2+(1/(4t))*x と解釈して解答しました．

(問題1)
xを固定したときの，
tの関数 f(t)=2*t*x-t^2 (t≧0)の取り得る値の範囲を調べる．

f(t)
=2*t*x-t^2
=-(t-x)^2+x^2．

t が t≧0 の範囲を動くとき，
f(t)取り得る値の範囲は，
x≧0のとき：f(t)≦x^2，
x＜0のとき：f(t)≦f(0)=0．

(問題2)
xを固定したときの，
tの関数 f(t)=t*x^2+(1/(4t))*x (t＞0)
の取り得る値の範囲を調べる．

(d/dt)f(t)=x^2-x/(4*t^2)．

x＜0のとき：
(d/dt)f(t)＞0，
lim[t→+0]f(t)=-∞，lim[t→∞]f(t)=∞．
よって f(t)の取り得る値の範囲は -∞＜f(t)＜∞．

x＞0のとき：
(d/dt)f(t)の符号は t=(1/(2*√x)) を境にして
マイナスからプラスになる．
lim[t→+0]f(t)=∞，lim[t→∞]f(t)=∞．
よって f(t)の取り得る値の範囲は
 f(t)≧f(1/(2*√x))=√(x^3)．

x=0のとき：
このとき，f(t)=0．

(問題3)
xを固定したときの，
tの関数 f(t)=x^3-4*t*x^2+2*t^2*x (t≧0)
の取り得る値の範囲を調べる．

f(t)
=x^3-4*t*x^2+2*t^2*x
=2*x*(t-x)^2-x^3．

x＜0のとき：
f(t)の取り得る値の範囲は
f(t)≦f(0)=x^3．

x＞0のとき：
f(t)の取り得る値の範囲は
f(t)≧-x^3．

x=0のとき：
このとき，f(t)=0．

(問題4)
自然数Ｎについて，Ｎの正の約数の個数と，Ｎ以下でＮと互いに素な
数の個数とが一致するような自然数Ｎは，N=1を除けば，
N=3, 8, 10, 18, 24, 30 の6個のみ．(答)

任意の素数 p と任意の正整数 a を変数とする
2変数関数 f(p，a) を次のように定める．
f(p,a)=((p-1)/(a+1))*p^(a-1)．

f(p,a)は p の狭義単調増加関数であり，
なおかつ a の狭義単調増加関数でもある．

f(p,a)のいくつかの値は次．
f(2,1)=1/2　f(3,1)=1    f(5,1)=2     f(7,1)=3
f(2,2)=2/3  f(3,2)=2    f(5,2)=20/3  f(7,2)=14
f(2,3)=1    f(3,3)=9/2  f(5,3)=25
f(2,4)=8/5  f(3,4)=54/5
f(2,5)=8/3

nを2以上の正整数とする．
正整数 n の素因数分解を，
n=Π[i=1..m](p[i])^(a[i]) (p[1]<p[2]<p[3]…，a[i]は正整数)
とする．
nの正の約数の個数をτ(n)，n以下の正整数で，nと互いに素なもの
の個数をφ(n)とすると，
τ(n)=Π[i=1..m](a[i]+1)，
φ(n)=n*Π[i=1..m](1-1/p[i])=Π[i=1..m](p[i]-1)*(p[i])^(a[i]-1)．

(主張)τ(n)=φ(n) を満たすような n の素因数は高々3個である．

(証明)
τ(n)=φ(n) を満たすような n が4個以上の素因数をもったとする．
nの素因数分解は
n=Π[i=1..m](p[i])^(a[i]) (p[1]<p[2]<p[3]…，a[i]は正整数，mは4以上の整数)
とできる．τ(n)=φ(n)より，
Π[i=1..m](a[i]+1)=Π[i=1..m](p[i]-1)*(p[i])^(a[i]-1)．
両辺をΠ[i=1..m](a[i]+1)で割って，
1=Π[i=1..m]((p[i]-1)/(a[i]+1))*(p[i])^(a[i]-1)．
つまり，
Π[i=1..m]f(p[i],a[i])=1．
一方，i≧4なるとき，p[i]≧7．
ゆえに i≧4なるとき f(p[i],a[i])≧f(7,a[i])≧3＞1．
よって，
Π[i=1..m]f(p[i],a[i])＞Π[i=1..3]f(p[i],a[i])≧f(2,1)*f(3,1)*f(5,1)=1．
これは矛盾．(証明終)

τ(n)=φ(n) を満たすような n がちょうど3個の素因数をもつとき
を考える．
n の素因数分解を
n=((p[1])^(a[1]))*((p[2])^(a[2]))*((p[3])^(a[3])) (p[1]<p[2]<p[3]，a[1],a[2],a[3]は正整数)
とすると，τ(n)=φ(n)より，
f(p[1],a[1])*f(p[2],a[2])*f(p[3],a[3])=1
となる．これを満たすものは，
f(2,1)*f(3,1)*f(5,1)=1 のみ．
このとき，n=30．

τ(n)=φ(n)を満たすような n がちょうど2個の素因数をもつのは，
f(2,1)*f(3,2)=1，
f(2,1)*f(5,1)=1，
f(2,3)*f(3,1)=1
の3通りのみ．
このとき，n=18,10,24．

τ(n)=φ(n)を満たすような n がちょうど1個の素因数をもつのは，
f(2,3)=1，
f(3,1)=1
の2通りのみ．
このとき，n=8，3．

https://oeis.org/A020488

＜水の流れ：丁寧で分かりやすい解法に感謝しています＞

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。