平成２８年１１月２７日

[流れ星]

　　　　　第340回数学的な応募解答

　　　　　　＜解答募集期間：10月30日〜11月27日＞

［逆関数の無限級数］

　皆さんは三角関数sinx , cosx の無限級数はマクローリン展開（ｘ＝０でのテイラー展開）をして表せることはよく知られています。

では、sinx , cosx　の逆関数　arcsinx , arccosx を無限級数で表してください。

NO1「uchinyan」 10/30 13時43分　受信

「uchinyan」 10/30 15時11分　受信 更新 11/27

第３４０回数学的な応募問題

一般に，関数 y = f(x) のマクローリン展開は，f(x) の n 階導関数を f^{n}(x) として，

y = f(x) = Σ[n=0,∞]{f^{n}(0)/n! * x^n}，

と無限級数で書けます。そこで，f^{n}(0) を求めればいいことになります。

まず，y = f(x) = arcsin(x) を考えます。

これは y = sin(x) の逆関数で，x = 0 の回りで考えればいいので，

x = sin(y)，dx/dy = cos(y)，

f^{1}(x) = f'(x) = dy/dx = 1/cos(y) = 1/√(1 - (sin(y))^2) = 1/√(1 - x^2)，

f^{2}(x) = (f'(x))' = x/(√(1 - x^2))^3 = x/(1 - x^2) * f^{1}(x)，

(1 - x^2) * f^{2}(x) = x * f^{1}(x)，

ここで，n 階導関数に関するライプニッツの公式を使うと，

(1 - x^2) * f^{n+2}(x) + nC1 * (1 - x^2)' * f^{n+1}(x) + nC2 * (1 - x^2)'' * f^{n}(x)

= x * f^{n+1}(x) + nC1 * x' * f^{n}(x)，

(1 - x^2) * f^{n+2}(x) - 2nx * f^{n+1}(x) - n(n-1) * f^{n}(x) = x * f^{n+1}(x) + n * f^{n}(x)，

(1 - x^2) * f^{n+2}(x) = (2n+1)x * f^{n+1}(x) + n^2 * f^{n}(x)，

x = 0 とおくと，

f^{n+2}(0) = n^2 * f^{n}(0)，f^{0}(0) = f(0) = 0，f^{1}(0) = f'(0) = 1，

で，k を 0 以上の整数として，

f^{2k}(0) = 0，f^{2k+1}(0) = ((2k-1) * (2k-3) * … * 3 * 1)^2，

です。そこで，

arcsin(x) = Σ[k=0,∞]{((2k-1) * (2k-3) * … * 3 * 1)^2/(2k+1)! * x^(2k+1)}，

となります。これの表記法はいろいろあるでしょうが，例えば，

arcsin(x) = Σ[k=0,∞]{((2k-1) * (2k-3) * … * 3 * 1)/(2^k * k! * (2k+1)) * x^(2k+1)}，

とか，

arcsin(x) = Σ[k=0,∞]{(2k)!/(4^k * (k!)^2 * (2k+1)) * x^(2k+1)}，

とか，もいいかも知れません。

こんな方法も。

y = arcsin(x)，x = sin(y)，dx/dy = cos(y)，

dy/dx = 1/cos(y) = 1/√(1 - (sin(y))^2) = 1/√(1 - x^2)，までは同じ。

ここで，f(x) = 1/√(1 - x) のマクローリン展開を考えると，

f^{n}(x) = ((2n-1) * (2n-3) * … * 3 * 1)/2^n * 1/(√(1 - x))^(2n+1)，より，

f(x) = Σ[n=0,∞]{((2n-1) * (2n-3) * … * 3 * 1)/(2^n * n!) * x^n}，

そこで，

dy/dx = 1/√(1 - x^2) = Σ[n=0,∞]{((2n-1) * (2n-3) * … * 3 * 1)/(2^n * n!) * x^(2n)}，

これより，y(0) = arcsin(0) = 0 なので，

arcsin(x) = y = ∫[0,x]{dy/dt}dt

= Σ[n=0,∞]{((2n-1) * (2n-3) * … * 3 * 1)/(2^n * n! * (2n+1)) * x^(2n+1)}，

になります。これは，先ほどの２番目の表記で k -> n としたものです。

次に，y = arccos(x) です。

これは，y = arcsin(x) が分かってしまえば簡単です。何故なら，

y = arccos(x)，x = cos(y) = sin(π/2 - y)，

x = 0 の回りで考えればいいので，

arcsin(x) = π/2 - y = π/2 - arccos(x)，

arccos(x) = π/2 - arcsin(x)，

arccos(x) = π/2 - Σ[k=0,∞]{((2k-1) * (2k-3) * … * 3 * 1)^2/(2k+1)! * x^(2k+1)}，

になります。

(感想)

久しぶりの理系数学の問題でしたね。

この手の問題は昔よく解きました。よい復習になりました。

計算の工夫はいろいろとありそうですが，まぁ，いいでしょう。

NO2「浜田明巳」 　　11/02 14時05分　受信 更新 11/05

　ｆ(ｘ)＝arcsinｘ，−１≦ｘ≦１，−π／２≦ｆ(ｘ)≦π／２
とすると，ｆ(０)＝０
　ｙ＝ｆ(ｘ)とすると，
　　ｘ＝sinｙ，−π／２≦ｙ≦π／２
　　∴ｄｘ／ｄｙ＝cosｙ＝(１−sin^２ｙ)^１／２＝(１−ｘ^２)^１／２（∵cosｙ≧０）
　　∴ｄｙ／ｄｘ＝(１−ｘ^２)^−１／２＝ｆ'(ｘ)

　ここで，
　　(１＋ｘ)^ａ＝１＋ａ／１！・ｘ＋{ａ(ａ−１)}／２！・ｘ^２＋{ａ(ａ−１)(ａ−２)}／３！・ｘ^３＋{ａ(ａ−１)(ａ−２)(ａ−３)}／４！・ｘ^４＋・・・
　　∴(１−ｘ^２)^−１／２＝１＋(−１／２)／１！・(−ｘ^２)＋{(−１／２)(−１／２−１)}／２！・(−ｘ^２)^２
　　　　　　　　　　　　　　＋{(−１／２)(−１／２−１)(−１／２−２)}／３！・(−ｘ^２)^３
　　　　　　　　　　　　　　＋{(−１／２)(−１／２−１)(−１／２−２)(−１／２−３)}／４！・(−ｘ^２)^４＋・・・
　　　　　　　　　　　　＝１＋１／(２・１！)・ｘ^２＋(１・３)／(２^２・２！)・ｘ^４＋(１・３・５)／(２^３・３！)・ｘ^６＋(１・３・５・７)／(２^４・４！)・ｘ^８＋・・・
　　∴ｆ(ｘ)＝arcsinｘ
　　　　　　＝∫_{ｔ：０→ｘ}(１−ｔ^２)^−１／２ｄｔ＋ｆ(０)
　　　　　　＝ｘ＋１／(２・１！・３)・ｘ^３＋(１・３)／(２^２・２！・５)・ｘ^５＋(１・３・５)／(２^３・３！・７)・ｘ^７＋(１・３・５・７)／(２^４・４！・９)・ｘ^９＋・・・

　ｙ＝arccosｘ，−１≦ｘ≦１，０≦ｙ≦πとすると，
　　ｘ＝cosｙ＝sin(π／２−ｙ)
　　∴π／２−ｙ＝arcsinｘ
　　∴ｙ＝arcosｘ
　　　　＝π／２−arcsinｘ
　　　　＝π／２−ｘ−１／(２・１！・３)・ｘ^３−(１・３)／(２^２・２！・５)・ｘ^５−(１・３・５)／(２^３・３！・７)・ｘ^７
　　　　　　−(１・３・５・７)／(２^４・４！・９)・ｘ^９−・・・

「浜田明巳」 　　11/05 09時50分　受信 更新 11/05

ｙ＝arcsinｘ

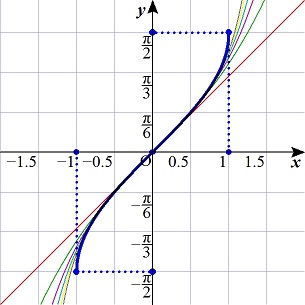
ｙ＝arccosｘ

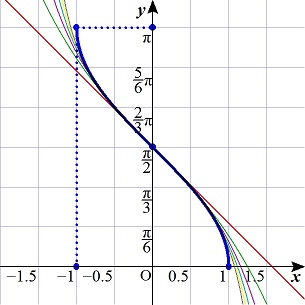
　いずれも元の関数のグラフに収束していく様子がうかがえる．

NO3「二度漬け白菜」 11/16 23時20分　受信

「二度漬け白菜」 11/16 23時20分　受信 更新 11/27

-1≦x≦1において，arcsin(x),arccos(x)はそれぞれ次のような収束する無限級数で表すことができる．

arcsin(x)=x+(1/2)*x^3/3+(1*3/(2*4))*x^5/5+ … +(1*3*5*…*(2*n-1)/(2*4*6*…*(2*n)))*x^(2*n+1)/(2*n+1)+…

arccos(x)=π/2-x-(1/2)*x^3/3-(1*3/(2*4))*x^5/5- … -(1*3*5*…*(2*n-1)/(2*4*6*…*(2*n)))*x^(2*n+1)/(2*n+1)-…

以下，この無限級数表示を導くに至った過程を記す．

xの関数f(x)をxでn回微分したものを f^{n}(x) と表す．
また，実数pと非負整数kに対し，
comb(p,k)=p*(p-1)*(p-2)*…*(p-k+1)/k! とする．

次の [補題]および[定理]を用意しておく．

---------------------------------------------

[補題]
f(x),φ(x) は [a,b]で連続，　
f^{k}(x)，φ^{k}(x) (k=1,2,…,n-1) は [a,b)において連続で，
f^{n}(x),φ^{n}(x)は(a,b)において存在するとし，且つ φ^{n}(x)≠0 とする．

F=f(b)-f(a)-Σ[k=1,n-1]f^{k}(a)*(b-a)^k/(k!),
G=φ(b)-φ(a)-Σ[k=1,n-1]φ^{k}(a)*(b-a)^k/(k!)　(ただし G≠0)
とすれば，
F/G = f^{n}(ξ)/φ^{n}(ξ), a<ξ<b
となるようなξが存在する．

(証明)
K=F/G とおく．
ψ(x)=f(x)-f(a)-Σ[k=1,n-1]f^{k}(a)*(x-a)^k/(k!)-K*(φ(x)-φ(a)-Σ[k=1,n-1]φ^{k}(a)*(x-a)^k/(k!))
とおけば，ψ(x)は[a,b]で連続，(a,b)で微分可能となり，ψ(a)=ψ(b)=0.
よってロルの定理より，ψ^{1}(η)=0, a<η<b なる η が存在する．
ψ^{1}(η)を計算すれば，
0=f^{1}(η)-Σ[k=1,n-1]f^{k}(a)*(η-a)^(k-1)/(k-1)!
-K*(φ^{1}(η)-Σ[k=1,n-1]φ^{k}(a)*(η-a)^(k-1)/(k-1)!). ---(☆)

ここで，
A(x)=f^{1}(η)-Σ[k=1,n-1]f^{k}(x)*(η-x)^(k-1)/(k-1)!，
B(x)=φ^{1}(η)-Σ[k=1,n-1]φ^{k}(x)*(η-x)^(k-1)/(k-1)!
とおく．
A(x),B(x)にコーシーの平均値定理を適用する．
(A(η)-A(a))/(B(η)-B(a))=A^{1}(ξ)/B^{1}(ξ), a<ξ<η なる ξ が存在する．
つまり，
(f^{1}(η)-Σ[k=1,n-1]f^{k}(a)*(η-a)^(k-1)/(k-1)!)/(φ^{1}(η)-Σ[k=1,n-1]φ^{k}(a)*(η-a)^(k-1)/(k-1)!)
=f^{n}(ξ)/φ^{n}(ξ), a<ξ<η なる ξ が存在する．
よって(☆)とから，
K=f^{n}(ξ)/φ^{n}(ξ), a<ξ<η
となる．
(証明終)

----------------------------------------------

[定理]
f(x)は[a,b]で連続，
f^{1}(x), f^{2}(x),…,f^{n-1}(x)は[a,b)で連続，
f^{n}(x)は(a,b)で存在すれば，次の関係が成立するような p,θ
が存在する．

f(b)=f(a)+Σ[k=1,n-1]f^{k}(a)*(b-a)^k/(k!) + R(n),
R(n)=(1-θ)^(n-p)*(b-a)^n*f^{n}(a+θ*(b-a))/(p*(n-1)!),
pは整数ではないような正の実数, 0<θ<1.

(証明)
φ(x)=(b-x)^p (pは整数ではないような正の実数) とおくと，
φ(b)=0,φ(a)=(b-a)^p,φ^{k}(a)=(-1)^k*comb(p,k)*k!*(b-a)^(p-k) となる．
よって，
φ(b)-φ(a)-Σ[k=1,n-1]φ^{k}(a)*(b-a)^k/(k!)
=-(b-a)^p*(1+Σ[k=1,n-1](-1)^k*comb(p,k))
=(b-a)^p*(-1)^n*comb(p-1,n-1)
となる．

よって先の補題より，
f(b)-f(a)-Σ[k=1,n-1]f^{k}(a)*(b-a)^k/(k!)
=f^{n}(ξ)*(b-a)^p*(-1)^n*comb(p-1,n-1)/((-1)^n*comb(p,n)*n!*(b-ξ)^(p-k))
=(b-a)^p*(b-ξ)^(n-p)*f^{n}(ξ)/(p*(n-1)!)
なる ξ (a<ξ<b) が存在する．
ここで，θ=(ξ-a)/(b-a) とおけば，0<θ<1 であって，
(b-a)^p*(b-ξ)^(n-p)*f^{n}(ξ)/(p*(n-1)!)
=(1-θ)^(n-p)*(b-a)^n*f^{n}(a+θ*(b-a))/(p*(n-1)!)
となる. すなわち，
f(b)=f(a)+Σ[k=1,n-1]f^{k}(a)*(b-a)^k/(k!)+(1-θ)^(n-p)*(b-a)^n*f^{n}(a+θ*(b-a))/(p*(n-1)!),
0<θ<1.
(証明終)

この定理でa=0,b=xとおくと，
f(x)=f(0)+Σ[k=1,n-1]f^{k}(0)*(x)^k/(k!) + R(n) ---(★)
R(n)=(1-θ)^(n-p)*x^n*f^{n}(θ*x)/(p*(n-1)!),
pは整数ではないような正の実数, 0<θ<1.
となる．

-----------------------------------------------

sin(y)は[-π/2,π/2]で狭義単調増加な連続関数であり，
sin(-π/2)=-1,sin(π/2)=1であるから，
[-1,1]で定義された連続な逆関数 y=arcsin(x) が確かに存在する．

y=arcsin(x) ⇔ x=sin(y).
y=arcsin(x)において，
dy/dx=1/(dx/dy)=1/cos(y)=(1-x^2)^(-1/2) (-1＜x＜1).

f(x)=arcsin(x) (0≦x≦1) とおく．
0≦x＜1のとき，
f^{1}(x)=(1-x^2)^(-1/2)，f^{2}(x)=x*(1-x^2)^(-3/2) から帰納的に
f^{n}(x)=P[n](x)*(1-x^2)^(-n+1/2) ---(★★)
 ( P[n](x) はxのn-1次の整式 )
となることが判る．

(1-x^2)*f^{2}(x)=x*f^{1}(x)
が成り立っていることが確認できる．
この式の両辺をxでn回微分すると，
(1-x^2)*f^{n+2}(x)-2*n*x*f^{n+1}(x)-n*(n-1)*f^{n}(x)=x*f^{n+1}(x)+n*f^{n}(x).
つまり，
(1-x^2)*f^{n+2}(x)=(2*n+1)*x*f^{n+1}(x)+n^2*f^{n}(x).
これと(★★)とから，
P[n+2](x)=(2*n+1)*x*P[n+1](x)+n^2*(1-x^2)*P[n](x) ---(★★★)
が得られる．

P[1](0)=1，P[2](0)=0 であることと(★★★)とから，
P[2*m](0)=0，P[2*m+1](0)=(1*3*5*…*(2*m-1))^2
となることが判る．
よって，
f^{2*m}(0)=0，f^{2*m+1}(0)=(1*3*5*…*(2*m-1))^2
となる．

f(x)は[0,1]で連続，
f^{1}(x), f^{2}(x),…,f^{n-1}(x)は[0,1)で連続，
f^{n}(x)は(0,1)で存在する．
従って先の定理 および (★)より，0≦x≦1なる任意のxに対し，
f(x)
=f(0)+Σ[k=0,n-1]f^{2*k+1}(0)*x^(2*k+1)/(2*k+1)! + R(2*n+1)
=Σ[k=0,n-1](1*3*5*…*(2*k-1)/(2*4*6*…*(2*k))*x^(2*k+1)/(2*k+1) + R(2*n+1)
となる．

R(2*n+1)において p=1/2 とするとき，R(2*n+1)→0 (n→∞)となることを以下に示す．

f^{1}(x)=(1-x^2)^(-1/2)=((1+x)^(-1/2))*((1-x)^(-1/2)) であり，
これにライプニッツの公式を適用する．

(1+x)^(-1/2)をxでk回微分したもの ((1+x)^(-1/2))^{k} は，
((1+x)^(-1/2))^{k}=(-1)^k*(2^(-k))*(1*3*5*…*(2*k-1))*(1+x)^(-1/2-k).
(ただし，k=0のときは (1*3*5*…*(2*k-1))=1 とする)

また，(1-x)^(-1/2)をxで 2*n-k 回微分したもの ((1-x)^(-1/2))^{2*n-k} は，
((1-x)^(-1/2))^{2*n-k}=(2^(k-2*n))*(1*3*5*…*(4*n-2*k-1))*(1-x)^(-1/2+k-2*n)
(ただし，k=2*nのときは (1*3*5*…*(4*n-2*k-1)=1 とする)
である．

よってライプニッツの公式より，
f^{2*n+1}(x)
=Σ[k=0,2*n]comb(2*n,k)*((-1)^k/(2^n))*(1*3*5*…*(2*k-1))*(1*3*5*…*(2*n-2*k-1))
*(1+x)^(-1/2-k)*(1-x)^(-1/2+k-2*n)
=(2*n)!*(1-x^2)^(-1/2)*(1-x)^(-2*n)*Σ[k=0,2*n](-1)^k*A[k]*((1-x)/(1+x))^k.
( A[k]=((1*3*5*…*(2*k-1))/(2*4*6*…*(2*k)))*((1*3*5*…*(4*n-2*k-1))/(2*4*6*…*(4*n-2*k))) とおいた )

0＜A[k]＜1，および，
1＞A[0]＞A[1]＞A[2]＞…＞A[n]＜A[n+1]＜A[n+2]＜…＜A[2*n]＜1
がわかる．

R(2*n+1) において，p=1/2 とおけば，
|R(2*n+1)|=2*(1-θ)^(2*n+1/2)*x^(2*n+1)/(2*n)!*|f^{2*n+1}(θ*x)|
=2*x*((1-θ)/(1-θ*x))^(1/2)*(1+θ*x)^(-1/2)*(x*(1-θ)/(1-θ*x))^(2*n)*|Σ[k=0,2*n](-1)^k*A[k]*((1-θ*x)/(1+θ*x))^k|.

y=(1-θ*x)/(1+θ*x), S[k]=1-y+y^2- … +(-y)^k
とおけば，0≦S[k]≦1.

故に，

Σ[k=0,2*n](-1)^k*A[k]*((1-θ*x)/(1+θ*x))^k
=A[0]-A[1]*y+A[2]*y^2- … +A[2*n]*y^(2*n)
=A[0]*S[0]+A[1]*(S[1]-S[0])+A[2]*(S[2]-S[1])+ … +A[2*n]*(S[2*n]-S[2*n-1])
=S[0]*(A[0]-A[1])+S[1]*(A[1]-A[2])+ … +S[2*n-1]*(A[2*n-1]-A[2*n])+A[2*n]*S[2*n]
=Σ[k=0,2*n-1]S[k]*(A[k]-A[k+1])+A[2*n]*S[2*n]
≦Σ[k=0,n-1](A[k]-A[k+1])+Σ[k=n,2*n-1](A[k+1]-A[k])+A[2*n]
=A[0]-A[n]+A[2*n]-A[n]+A[2*n]
=3*A[0]-2*A[n] (∵A[2*n]=A[0]).

0≦2*x≦2, 0＜((1-θ)/(1-θ*x))^(1/2)≦1, 0＜(1+θ*x)^(-1/2)≦1,0≦(x*(1-θ)/(1-θ*x))^(2*n)≦1
であるから，
|R(2*n+1)|
≦2*|Σ[k=0,2*n](-1)^k*A[k]*((1-θ*x)/(1+θ*x))^k|
≦2*(3*A[0]-2*A[n])
＜6*A[0].

ここで，A[0]=(1*3*5* … *(4*n-1))/(2*4*6* … *(4*n)) → 0 (n→∞).
(A[0]=Π[k=1,2*n](1-1/(2*k))≦Π[k=1,2*n]e^(-1/(2*k)) (∵0≦xのとき，1-x≦e^(-x))
=e^(-(1/2)*Σ[k=1,2*n]1/k)→0(n→∞))
よって，0≦x≦1 に対して，|R(2*n+1)| → 0 が得られる．

以上より，0≦x≦1においてf(x)は
f(x)
=Σ[n=0,∞](1*3*5*…*(2*n-1)/(2*4*6*…*(2*n)))*x^(2*n+1)/(2*n+1)
=x+(1/2)*x^3/3+(1*3/(2*4))*x^5/5+ … +(1*3*5*…*(2*n-1)/(2*4*6*…*(2*n)))*x^(2*n+1)/(2*n+1)+…
と級数展開できる．
また，この式の両辺はいずれも奇関数であるから，xを-xに変えても
やはり等式が成り立つ．
よって-1≦x≦1においてf(x)は
f(x)=x+(1/2)*x^3/3+(1*3/(2*4))*x^5/5+ … +(1*3*5*…*(2*n-1)/(2*4*6*…*(2*n)))*x^(2*n+1)/(2*n+1)+…
と級数展開できる．

cos(y)は[0,π]で狭義単調減少な連続関数であり，
cos(0)=1,cos(π)=-1であるから，
[-1,1]で定義された連続な逆関数 y=arccos(x) が確かに存在する．
y=arcsin(x) とおくと，
sin(y)=x. よって，cos(π/2-y)=x.
-π/2≦y≦π/2 であるから 0≦π/2-y≦π.
よって，arccos(x)=π/2-y.
つまり，arccos(x)=π/2-arcsin(x).

よって -1≦x≦1 において arccos(x)は，
arccos(x)=π/2-x-(1/2)*x^3/3-(1*3/(2*4))*x^5/5- … -(1*3*5*…*(2*n-1)/(2*4*6*…*(2*n)))*x^(2*n+1)/(2*n+1)-…
と無限級数で表すことができる．

-----------------------------------------

今回の問題の解答の作成には，次の本を参考にしました．

藤原松三郎 著 『微分積分学 第一巻』

(この本の 第二章 を参考にしました．)

NO4「早起きのおじさん」 11/21 21時06分　受信 更新 11/27

関数 のマクローリン展開は、

という形をしています。

例えば、 のマクローリン展開は、

なので、

また、両辺を で微分すると、

グラフ

さて、 の逆関数 のマクローリン展開を考えます。

いくつか導関数を調べます。

なので、

よって、

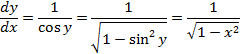
簡便のためにこれを

と表すことにします。

さらに続けると、

一般的に、次のように表してみます。

ここで係数の関連を調べると、

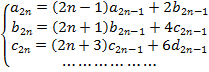
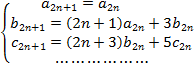
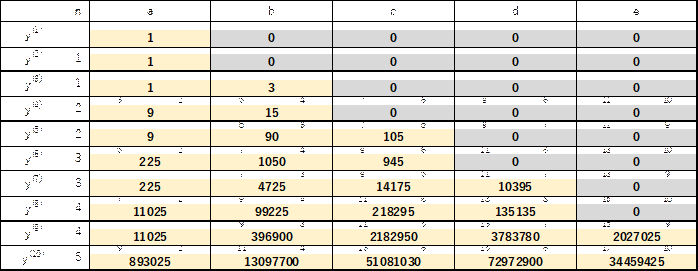
この関係から、次のように、 の式として整理したときの導関数の係数を求めることができます。

（実際にはエクセルで計算しました）

マクローリン展開を考えるとき、 とします。

すると、偶数次の導関数は0、奇数次の導関数も2番目以降の項は0になります。

よって、奇数の導関数の最初の項の係数の値が大切になります。

ここで、初めの2つの係数の仕組みを調べると、

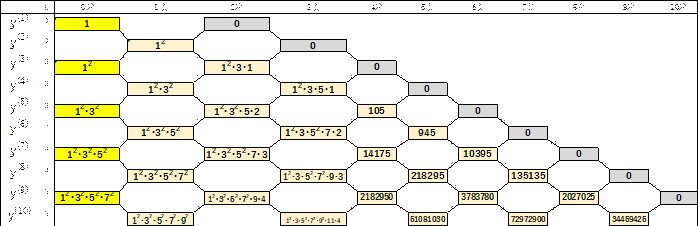
ここで、奇数次導関数を一般的に書いてみると（ と考えるのが係数の式が自然です）、

偶数次の導関数は、

と推察されます。

さて、奇数次の導関数（）の最初の項の係数が、 の形になることを調べます。

奇数と偶数をセットでみていきます。

［１］ のとき、

です。

です。

　これは、初めの計算と一致しています。

［２］ のとき、式（*）と（**）が成立すると仮定します。

式（**）の両辺を で微分すると、

となり、 のとき、(*)と（**）が成り立てば、 のときも奇数次の導関数の最初の係数は奇数平方の積の形です。

また、2番目の項の係数も仮定の形をしているので、 のときの偶数次の導関数の最初の係数も奇数平方の積の形です。

したがって、 のときの奇数次の導関数の最初の係数も奇数平方の積の形です。

（しかし、偶数次の係数が成立しているかはいえません。）

（偶数次の導関数の2番目の係数がこのままでは仮定の形に戻らないので）

（しかし、実際に計算すれば仮定の形になります。）

以上から答えは、

さて、 の逆関数 のマクローリン展開を考えます。

いくつか導関数を調べます。

なので、

よって、

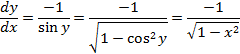
簡便のためにこれを

と表すことにします。

すると、今まで考えていた正弦関数の逆関数のときと同じ形です。

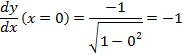
に注意して、

この結果から、

です。

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。