平成29年6月11日
 [流れ星]
[流れ星]
第347回数学的な応募解答
<解答募集期間:5月14日〜6月11日>
[ガウス記号2017]

追加の遊び問題
1から6までの各数字を1回ずつ用いて、結果が2017となる式を作ってください。
使用できる演算は+、−。×、÷ と 括弧( )とします。
例 2017=42×6×(3+5)+1
NO1「uchinyan」
05/14 12時56分 受信 更新 6/11
a(n) = [n^2/2017],1 <= n <= 2017,において,
n^2/2017 の隣同士の差,n^2/2017 - (n-1)^2/2017 = (2n-1)/2017,を考えます。
隣同士の差が 1 未満,(2n-1)/2017 < 1,1 <= n <= 1008 <
1009,の場合
この場合は,a(n) の隣同士が同じ値か差が 1 なので,
a(n) は a(1) = [1/2017] = 0 〜 a(1008) =
[1008^2/2017] = 503 のすべての整数の値を取ります。
つまり,0 〜 503
の 504 種類の値を取ります。
隣同士の差が 1 以上,(2n-1)/2017 >= 1,1009 <= n <= 2017,の場合
この場合は,a(n) の隣同士の差が 1 以上なので,a(n) の値はすべて異なり,
a(n) の項数と同じ 2017 - 1008 = 1009 種類の整数の値を取ります。
以上ですべてなので,取り得る整数の値は,504 + 1009 =
1513 種類,になります。
追加の遊び問題
いろいろとできるのだろうなと思うものの,
あまり興味がそそられないので,ある意味美しいものを1つだけ。
2017=1+(2+34)×56。
(感想)
この問題は以前に類題を解いたことがあります。
2017 をもっと小さな値にし n = 1, 2, 3, ... として傾向を調べればいいですね。
NO2「早起きのおじさん」 05/18 18時51分 受信 更新 6/11
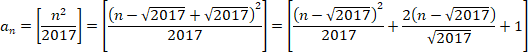
ここで、 ![]() とおきます。
とおきます。
次の2次関数を考えます。
![]()
![]()
この2次関数の微分係数が1未満のところを調べます。
(つまり、yの増加が1より小さいところ見つけます)
![]()
とおくと、
![]()
つまり、n=1008より小さいところは、数列の値の増加が多くても1です。
それ以降は、数列の増加は少なくても1です。
![]()
![]()
![]()
![]()
![]()
初項から第1008項まで、この数列は、503−0+1=504種類の値をとります。
第1009項から第2017項まで、この数列は、2017−1009+1=1009種類の値をとります。
よって、504+1009=1513種類の整数があります。
追加の問題
2017は、素数です。
例えば、
![]()
![]()
NO3「スモークマン」 05/18
20時03分 受信 更新 6/11
上手い方法思いつけず…^^;
n<=√(m*2017)<n+1
m=1
44<√2017<45
45<=√(m*2017)<1009
m=1〜504・・・504個
1009*2=2018>2017 ので、
たとえば…
追加遊び問題
65*31+4÷2=2017
NO4「二度漬け白菜」 05/31
21時31分 受信 更新 6/11
この数列の中には 1513 種類の整数が存在する.(答)
(n+1)^2/2017 - n^2/2017 = (2*n+1)/2017 である.
s(n)=(2*n+1)/2017 とおく.
n≧1008を満たすような n に対しては,
s(n)≧1 であるので,a(n+1)>a(n).
よって,a(1008),a(1009),a(1010),…,a(2017)
は,全て異なる値をとる.
また,n≦1007を満たすような n に対しては,
s(n)<1 であるので,a(n+1)≦a(n)+1.
よって,a(1),a(2),a(3),…,a(1008)
は全体として,a(1) 以上 a(1008)以下の全ての
整数値をとる.
よって,数列 a(1),a(2),a(3),…,a(2017)
に現れる数値の種類は,
(a(1008)-a(1)+1) + (2017-1008)
=(503-0+1) + 1009
=1513 種類.
追加の遊び問題:
和が2017となる式には次のような
ものがあります.
2017=1+(2+34)*56.
2017=1+(32+4)*56.
2017=1+(2+54)*36.
2017=1+(4+52)*36.
2017=4+61*(35-2).
2017=31*65+4-2.
2017=31*65+4/2.
和が2018,2019,2020となる式も
考えてみました.
2018=2+6*(341-5).
2019=4+(32-1)*65.
2020=4+3*12*56.
2020=4*(513-2-6).
ガウス記号に関する問題をひとつ紹介しておきます.
[問題]
実数xに対して,xを超えない最大の整数を floor(x)
と表すことにします.
nを正の整数とするとき,和
Σ[k=1〜n^2](floor((k/n)^2) + floor(n*k^(1/2)))
を n の式で表すとどうなるか?
「皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。
