平成29年11月26日
 [流れ星]
[流れ星]
第353回数学的な応募解答
<解答募集期間:10月29日~11月26日>
[存在する範囲]
過去の大学入試問題です。次のことを参考にして解いてください。
問題1は与式を同時に満たすy、zの組が存在するためのxの条件を求める。
問題2は与式を満たす実数x、y(x≠y)の組が存在するためのkの条件を求める。
ここから、問題です。
NO1「早起きのおじさん」 11/07 16時03分 受信 更新
「早起きのおじさん」 11/08 11時11分 受信
更新 11/26
問題1
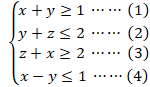
4つの式を同時に考えるのは、難しいので少しずつ考えます。
それぞれの式は、空間を平面で分けた一方を表します。
各不等式は、次の様です。
(1) ![]() (2)
(2)![]()
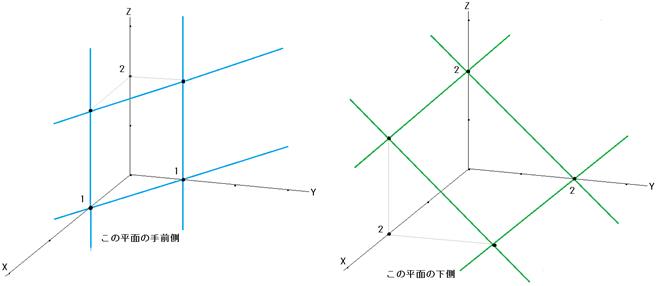
図A 図B
(3) ![]() (4)
(4)![]()
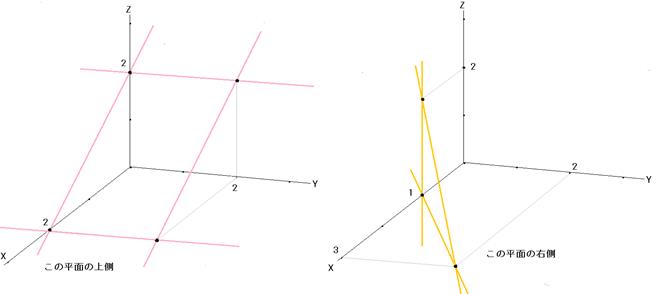
図C 図D
さて、4つのうち3つを同時に考えてみます。
(直線に添えてあるのは、どの2つの平面の交線かを示します)

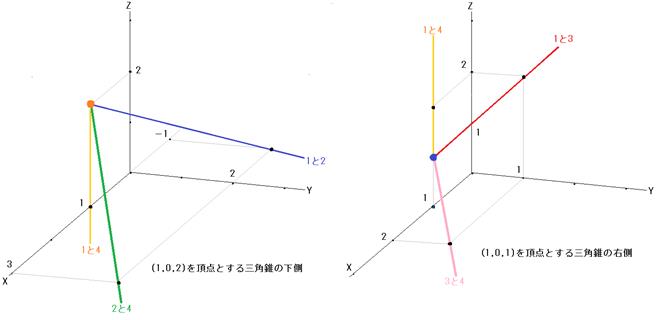
図E 図F

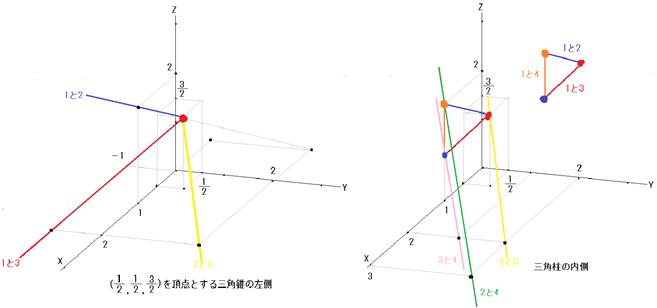
図G 図H
3つずつを同時に考えると、図E、図F、図G、図Hのようになります。
さて、4つを同時に考えるには、図Hの中に(1)の不等式の要素を加味します。
すると、図Hの三角形で、三角柱が切られることになります。
三角形の頂点の座標は、
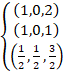
よって、![]() であることが、分かります。
であることが、分かります。
問題2
![]()
式(1)において、xとyとを入れかえると、式(2)になるので、互いに逆関数の関係です。
グラフをかくと、2つは、直線y=xに関して対称になります。
式(1)のグラフを赤、式(2)のグラフを青でかいてみます。
kの値により、いろいろな場合があります。
○kが正で値が大きいとき、2つは4つの点を共有します。
うち2つは、x と y
の値が異なり、条件をみたします。
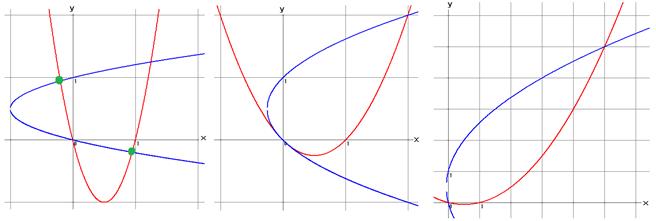
図A (1)と(2)が4点で交わる 図B (1)と(2)が原点で接する 図C (1)と(2)が2点で交わる
式(1)において、
![]()
![]()
なので、(1)のグラフの原点での、微分係数は、x=0として、-kです。
(2)のグラフは、(1)の逆関数なので、-kの逆数をとって、原点での微分係数は、![]() です。
です。
図Bの場合を考えます。
![]()
とすると、
![]()
![]()
より、k=1のとき、2つのグラフは、原点で接します。
○k=0のときは、x=y=0なので、条件をみたしません。

図D
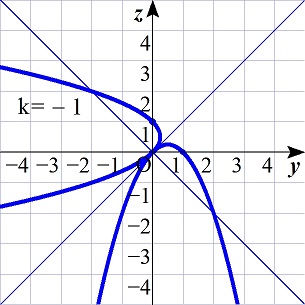
○kが負の値をとる場合を考えます。
上の計算から、k=-1のとき、2つのグラフは接します。(図F)
また、y=x上では、
![]()
![]()
![]()
![]()
x=0は、原点なので、![]() のときの微分係数は、(3)に代入して、
のときの微分係数は、(3)に代入して、
![]()
(2)のグラフは、(1)の逆関数なので、逆数をとって、![]() 上での微分係数は、
上での微分係数は、![]() です。
です。
![]()
![]()
![]()
![]()
![]()
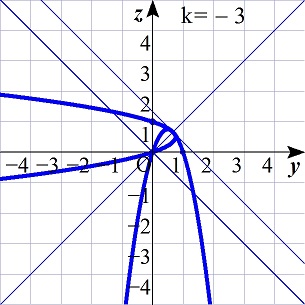
より、k=-3のとき、2つのグラフは、y=x上で接します。
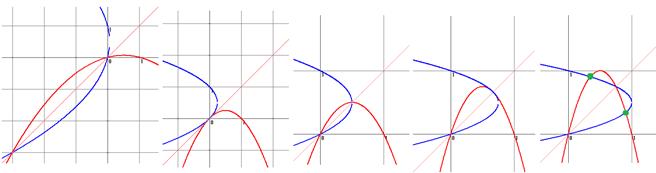
図E 2点で交わる 図F 原点で接する 図G 2点で交わる 図H y=x上で接する 図I 4点で交わる
まとめると、k>1,k<-3となります。
「早起きのおじさん」 11/15 22時14分 受信
更新 11/26
別解です。
問題1
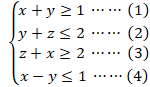
(4)を ![]() として、(1)に加え整理すると、
として、(1)に加え整理すると、![]()
この2式を合わせると、![]()
この条件と、(1)とで最小の ![]() を考えると、
を考えると、![]()
よって、![]()
問題2
![]()
(1)から(2)を引いて、整理すると、
![]()
ここでは、![]() を考えるので、
を考えるので、![]() で約して整理すると、
で約して整理すると、
(k=0のときも ![]() となるので、
となるので、![]() として考えます)
として考えます)
![]()
この直線と(1)を連立させて考えます。
○k>0でk=1のときを考えます。
![]()
下の左のグラフになります。
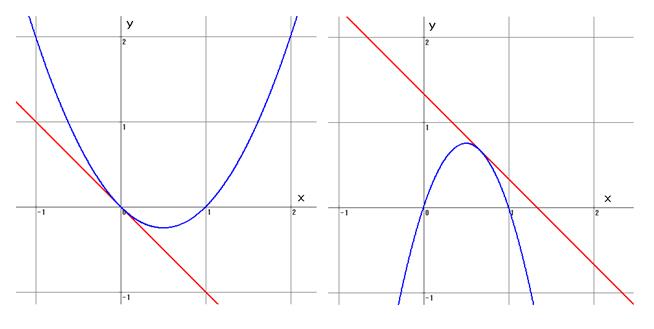
原点で2つのグラフは接します。
0<k<1のとき、赤の直線は、y切片が負になり、放物線と共有点がなくなります。
k>1のとき、赤の直線は、y切片が正になり、放物線と共有点が2つになります。
○k<0で=-3のときを考えます。
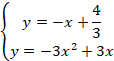
上の右のグラフになります。
![]() で2つのグラフは接します。
で2つのグラフは接します。
kが負で絶対値が大きくなると、赤の直線のy切片は1に近づくように、だんだん下がってきます。
kが負で絶対値が大きくなると、青の放物線の頂点は段々上がっていきます。
0>k>-3のとき、2つのグラフの共有点はありません。
-3>kのとき、2つのグラフの共有点が2つになります。
まとめると、k>1,k<-3となります。
NO2「浜田明巳」 11/07 17時21分 受信 更新 11/26
問題1
x+y≧1・・・(1)
y+z≦2・・・(2)
z+x≧2・・・(3)
x-y≦1・・・(4)
(1),(4)から,y≧1-x,y≧x-1
∴y≧|x-1|・・・(5)
(3)から,z≧2-x・・・(6)
(2)より,点(y,z)の存在領域は,
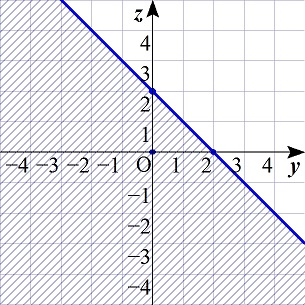
(5),(6)より,点(y,z)の存在領域は,
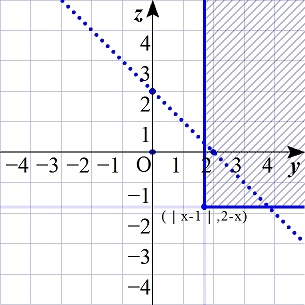
この2つの領域に共通部分があるので,点(|x-1|,2-x)が,不等式(2)を満たせばよい.
∴|x-1|+(2-x)≦2
∴|x-1|≦x
∴-x≦x-1≦x
∴x≧1/2・・・(答)
問題2
y=k(x2-x)・・・(1)
x=k(y2-y)・・・(2)
xy平面で考える.
k=0のとき,(x,y)=(0,0)となり,直線y=x上のみに共有点がある.
∴k≠0
(1)から,
y=k{(x-1/2)2-1/4}
これは,頂点(1/2,-k/4)の放物線を表す.
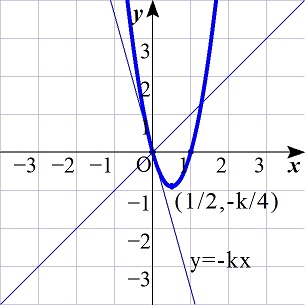
同様に,(2)から,
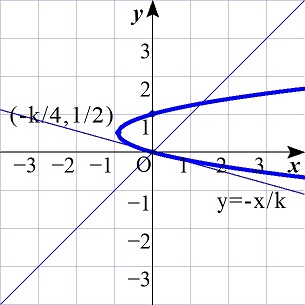
0<k<1,k=1,k>1のときのグラフを考えると,
k>1
のとき,条件を満たすことが分かる.
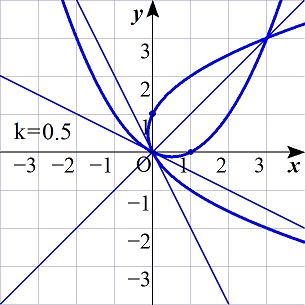
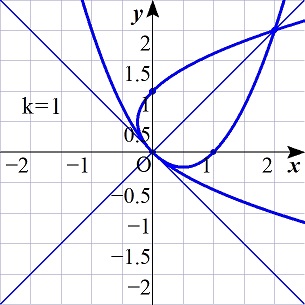
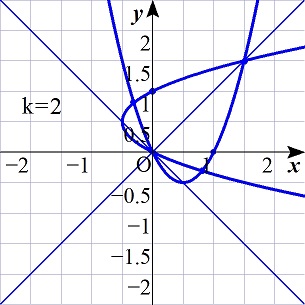
k<0のときを考える.
(1),(2)より,
dy/dx=k(2x-1),dx/dy=k(2y-1)
(1),(2)上の点(p,p)(p≠0)における接線の傾きが-1に等しいとき,
k(2p-1)=-1,1/{k(2p-1)}=-1
∴p=(1-1/k)/2=(k-1)/(2k)・・・(3)
p=k(p2-p),p≠0から,
1=k(p-1)
∴p=1/k+1=(k+1)/k
(3)から,
(k-1)/(2k)=(k+1)/k
∴k-1=2(k+1)
∴k=-3
これはk<0を満たす.
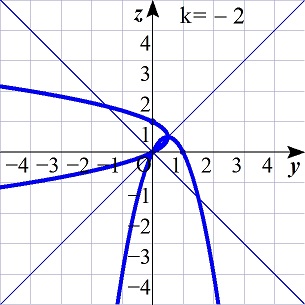
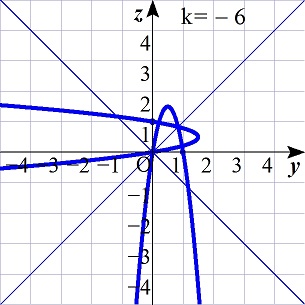
-1<k<0,k=-1,-3<k<-1,k=-3,k<-3のときのグラフを考えると,
k<-3
のとき,条件を満たすことが分かる.
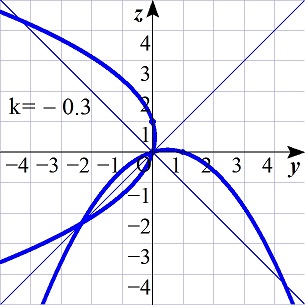
まとめると,
k<-3,1<k
「浜田明巳」 11/08 10時47分 受信 更新 11/26
問題2(別解)
グラフ表示ソフトGRAPESを使って解く.
y=k(x2-x)・・・(1)
x=k(y2-y)・・・(2)
(2)を(1)に代入すると,
x=k{k2(x2-x)2-k(x2-x)}
∴x=0 または 1=k{k2(x3-2x2+x)-k(x-1)}・・・(3)
x=0のとき,(1)から,y=0
故にx=yとなり,条件に反する.
故にx≠0であり,(3)の後半から,
k3x3-2k3x2+k2(k-1)x+(k2-1)=0・・・(4)
(4)の左辺をf(x)とおく.
k=0とすると,-1=0となり,矛盾するので,
k≠0
xの3次方程式f(x)=0の実数解を
x1,x2,x3(x1≦x2≦x3)
とする(GRAPESの関数sol(f(x)=0,i)(i=1,2,3)を使用し求める).
それらのxの値に対して,(1)上の点を,
(x1,y1),(x2,y2),(x3,y3)
とする.
これらの点のどれか1個でも直線y=x上にないとき(|xi-yi|>0.01,i=1,2,3),点
(k,-4)
を画面上に記入する.
-10≦k≦10で,0.05きざみで計算し,次の図を得る.
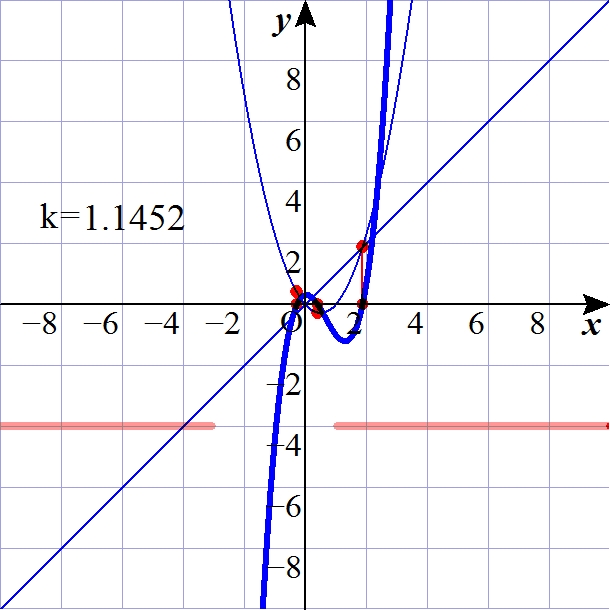
この図から,
k<-3,1<k
となることが分かる.
NO3「二度漬け白菜」 11/16
09時52分 受信 更新 11/26
問題1:
与えられた4つの不等式を同時に満たすy,zの組が存在するような
xの範囲は,x≧1/2 (答)
x+y≧1 --- ①
y+z≦2 --- ②
z+x≧2 --- ③
x-y≦1 --- ④
x<1/2のとき,①~④を同時に満たすようなy,zの組は存在しない.
なぜなら,
x<1/2のとき,①~④を同時に満たすようなy,zの組(Y,Z)が存在
すると仮定する.このとき,
②より,Y+Z≦2 --- ⑤
①+③より,2*x+Y+Z≧3.よって,Y+Z≧3-2*x>2 (∵x<1/2)
しかし,これは⑤と矛盾する.
x≧1/2のとき,①~④を同時に満たすような y,z の組は
必ず存在する.
y=x,z=2-x とすればよい.
実際,y=x,z=2-x としたとき,
x+y=x+x=2*x≧1,
y+z=x+(2-x)=2≦2,
z+x=(2-x)+x=2≧2,
x-y=x-x=0≦1
となるから,①~④を同時に満たしている.
問題2:
題意を満たすような実数 k の範囲は,
k<-3 または 1<k (答)
y=k*(x^2-x) --- ①
x=k*(y^2-y) --- ②
k=0 は題意を満たさない.
k≠0 として考える.
2曲線①,②は直線 y=x に関して対称.
よって題意の交点は直線 y=x に垂直な直線上に
2個ある.この直線を y=-x+2*t とすると,
2交点のx座標を
t-a,t+a (0<a)
とおくことができる.
xの2次方程式
-x+2*t=k*(x^2-x)
が,異なる2解 t-a, t+a をもつ条件を求めればよい.
この条件は,解と係数の関係より,
2*t=(k-1)/k, t^2-a^2=-2*t/k
を満たす t,a (0<a) が存在すること,
つまり,
a^2=(k-1)*(k+3)/(4*k^2) --- ③ (tの消去),
2*t=(k-1)/k
を満たす a,t (0<a) が存在することと同値で,
その条件は,③を満たす a (0<a) が存在すること
と同値.よって求めるkの範囲は,
k<-3 または 1<k (答)
以上
