�����R�O�N�P���Q�P��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@��355�����w�I�ȉ����
�@�@�@�@�@�@����W���ԁF12��24���`1��21����
�m2018��355�̖��n
�@2017�N���c��1�T�ԁB���܂ł̂�����ɐ[�����Ӑ\���グ�܂��B����2018�N���������������ڎ���܂��悤��낵�����肢�����܂��B
�U��Ԃ�A�ŏ��̉�����͐���P�X�X�W�N����10�N10���ł��āA���N21�N�ڂ��}���܂��B
�����ŁA���N�̐���2018�N�Ƒ�355����̐����ɂ��Ȃ�ŁA��₵�܂����B

NO1�u���N���̂�������v 12/25 16��13���@��M �X�V 1/21
���1
(1)
![]() �ł��B
�ł��B
100�́A������0���A2���т܂��B
10�̎w���̕������A0�����т܂��B
10�́A2��5�ɑf���������ł��܂��B
![]()
![]() �ł��B
�ł��B
�܂�A2��5�̏��Ȃ��ق��̈����̌������A������0�����т܂��B
�����A2��5�̈����̗l�q�����Ă݂܂��B
1 �@ 2��0�A5��0��
2 �@ 2��1�A5��0��
3 �@2��0�A5��0��
4 �@2��2�A5��0��
5 �@2��0�A5��1��
6 �@2��1�A5��0��
7 �@2��0�A5��0��
8 �@2��3�A5��0��
9 �@2��0�A5��0��
10 �@2��1�A5��1��
�E�E�E
5���2�̈����̕����A�������Ƃ�������܂��B
�i���Ȃ��Ƃ��A2��1�����A5��5�����Ɉ���������܂��j
����āA5�̈����̌��ׂ܂��B
5������5�̈����������̂ŁA
2018��5��403���3
����ɁA25������5�̈����������̂ŁA
403��5��80���3
����ɁA125������5�̈����������̂ŁA
80��5��16
����ɁA625������5�̈����������̂ŁA
16��5��3���1
����ȏ�A5�̈����͂Ȃ��̂ŁA
403�{80�{16�{3��502
502��0���A�����ɕ��т܂��B
(2)
��̖��ɂ���悤�ɁAn��5�Ŋ���A���̏���5�Ŋ��邱�Ƃ��J��Ԃ��āA���̘a�����v���܂��B
����ƁA�����ɕ���0�̌������܂�܂��B
n��8085�Ƃ���ƁA
8085��5��1617���0
1617��5��323���2
323��5��64���3
64��5��12���4
12��5��2���2
�m�F����ƁA
1617�{323�{64�{12�{2��2018
8090�́A0��2019���т܂��B
���2
![]()
�m�J�b�R�n�́A89�|18��71����܂��B
2018��71��28.422���
2018��28�~41�{29�~30
�m�J�b�R�n��42�Ԗڂ́A![]()
![]()
�䂦�ɁA![]()
����āA![]()
���3
(1)
���̖��̐���̒l�́A3�i�@�Ő�������킵���Ƃ��ɁA�e�ʂ̐������A0��1�ł���悤�Ȑ��ł��B
������A�ǂ����ɁA2���o�Ă���悤��3�i�@�ł���킳��鐔�͐���̒l�Ƃ��Č���܂���B
3�i�@�ŕ\���Ă݂�ƁA
|
3��n�� |
|
�� |
�q�ׂ̌� |
|||
|
|
1 |
1�� |
1�� |
|
||
|
|
10
11 |
2�� |
3�� |
|
||
|
|
100
101 110 111 |
4�� |
7�� |
|
||
|
|
1000
1001 1010 1011 1100 1101 1110 1111 |
8�� |
15�� |
|
||
|
�@�E�E�E |
�E�E�E |
�E�E�E |
�E�E�E |
|||
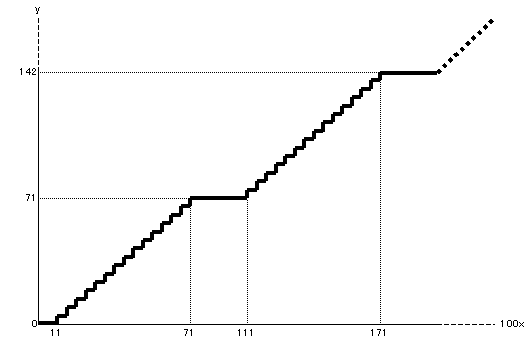
��̕\�̐����A2�i�@�̐��Ƃ��āA�݂�Ǝ��̂悤�ɂȂ�܂��B
|
1 |
|
|
|
2
3 |
|
|
|
4
5 6 7 |
|
|
|
8
9 10 11 12 13 14 15 |
|
|
|
�E�E�E |
|
�܂�A355�Ԗڂ̍����l����Ƃ��A2�i�@��355�Ԗڂ̐����l���A3�i�@�ɓǂݑւ���悢���ƂɂȂ�܂��B
355��2��177���1
177��2��88���1
88��2��44���0
44��2��22���0
22��2��11���0
11��2��5���1
5��2��2���1
2��2��1���0
�܂�A
355 (10)��101100011 (2)
�����3�i�@�̐��ɓǂݑւ���ƁA
![]()
(2)
(1)�Ƌt�̂��Ƃ�����悢�̂ŁA355��3�i�@�ŕ\���āA2�i�@�̐��Ƃ��čl���܂��B
355��3��118���1
118��3��39���1
39��3��13���0
13��3��4���1
4��3��1���1
�܂�A
355 (10)��111011 (3)
������A2�i�@�ƍl����ƁA
![]()
59�ԖڂɌ���܂��B
(3)
3�i�@�ŁB2018��\���ƁA
2018��3��672���2
672��3��224���0
224��3��74���2
74��3��24���2
24��3��8���0
8��3��2���2
2018 (10)��2202202 (3)
�܂�A
![]()
�W����2�̂Ƃ��낪�A5��������̂ŁA����3�̗ݏ��5�g�g��Ȃ��ƁA2018��\�����Ƃ��ł��܂���B
NO2�u�l�c�����v �@�@01/06 11��09���@��M �X�V 1/21
���P
�i�������߂���ł́C��͂�v���O�����̏o�Ԃ��낤�D�������w�Z����v���O����������n�߂�Ƃ̂��Ɓj
�@VBSCRIPT�ŋ��߂��D
�i�P�j�Q�O�P�W�I��f�������������Ƃ��́C�Q�̎w���ƂT�̎w���̂����́C�傫���Ȃ��������ƂȂ�D
�@���炩�ɂT�̎w���̕����������̂ŁC�T�̎w�������ƂȂ�D
�@�T����Q�O�P�T�̂T�̔{���ŁC�T�Ŋ��邱�Ƃ��ł���̑����v�����߂�悢�D
kosuu=0
for n=5 to 2015 step 5
nn=n
while nn mod 5=0
nn=nn/5
kosuu=kosuu+1
wend
next
msgbox kosuu
�@���̃v���O�����ɂ��C�T�O�Q�����ł���D
�i�Q�j���l�̃v���O�����ɂ��C�W�O�W�T�����ł���D
���Q
�@���l�̃v���O�����ɂ��C�Q�W�S�O�����ł���D
���R
�i�P�j����̑��قȂ�R�̗ݏ�̘a�ŕ\����鐔�����������ɕ��ׂ�����́C
�@�@�R�O�C�R�P�C�R�P�{�R�O�C�R�Q�C�R�Q�{�R�O�C�R�Q�{�R�P�C�R�Q�{�R�P�{�R�O�C�E�E�E
�ƂȂ�C�����̐��́C��i�@�ŕ\���ꂽ����C
�@�@�P�i�Q�j�C�P�O�i�Q�j�C�P�P�i�Q�j�C�P�O�O�i�Q�j�C�P�O�P�i�Q�j�C�P�P�O�i�Q�j�C�P�P�P�i�Q�j�C�E�E�E
�ƑΉ�����D
�@�܂��C
�@�@�R�T�T���Q�~�P�V�V�{�P���Q�~(�Q�~�W�W�{�P)�{�P���Q�Q�~(�Q�~�S�S)�{�Q�{�P
�@�@�@�@�@���Q�R�~(�Q�~�Q�Q)�{�Q�{�P���Q�S�~(�Q�~�P�P)�{�Q�{�P
�@�@�@�@�@���Q�T�~(�Q�~�T�{�P)�{�Q�{�P���Q�U�~(�Q�~�Q�{�P)�{�Q�T�{�Q�{�P
�@�@�@�@�@���Q�W�{�Q�U�{�Q�T�{�Q�{�P
�@�̂ɂR�T�T�Ԗڂ̍��́C
�@�@�R�W�{�R�U�{�R�T�{�R�{�P���U�T�U�P�{�V�Q�X�{�Q�S�R�{�R�{�P���V�T�R�V�E�E�E�i���j
�i�Q�j�R�T�T���R�~�P�P�W�{�P���R�~(�R�~�R�X�{�P)�{�P���R�Q�~(�R�~�P�R)�{�R�{�P
�@�@�@�@�@�@���R�R�~(�R�~�S�{�P)�{�R�{�P���R�S�~(�R�{�P)�{�R�R�{�R�{�P
�@�@�@�@�@�@���R�T�{�R�S�{�R�R�{�R�{�P
�ł��邩��C���߂�Ԑ��́C
�@�@�Q�T�{�Q�S�{�Q�R�{�Q�{�P���R�Q�{�P�U�{�W�{�Q�{�P���T�X�i�Ԗځj�E�E�E�i���j
�i�R�j���قȂ�R�̗ݏ�̘a�ŕ\����鐔�́C���̂Q��ނ���D
�@�@�R���P�{�R���Q�{�R���R�{�E�E�E�{�R�����{�R�O
�@�@�R���P�{�R���Q�{�R���R�{�E�E�E�{�R����
�@����������o�����p�͐���������Ȃ�C�������̂Ƃ��C�����������ł���D
�@���̂Q��ނ̐����R�Ŋ������]��́C�O�܂��͂P�ł���D
�@�Ƃ��낪�C�Q�O�P�W�߂Q�imod �R�j�ł���̂ŁC�Q�O�P�W�͂��̐�����ɂȂ��D
NO3�uKasama�v
01/08 19��59���@��M �X�V 1/21 �@
|
���P |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���Q |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���R |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
NO4�u��x�Ђ����v 01/12
10��58���@��M �X�V 1/21
���1�F
������ n �ɑ��āCn!/(10^m) �������ƂȂ�悤��
�ő�̐��� m �� f(n) �Ƃ���ƁCf(n)�͎����ŗ^��
����D
f(n)=��[k=1,��]floor(n/(5^k))�D
(1)
f(2018)
=floor(2018/5)+floor(2018/5^2)+floor(2018/5^3)+floor(2018/5^4)
=403+80+16+3
=502
�ł��邩��C2018!�̖�����0�� 502 ����(��)�D
(2)
f(8080)=2017,
f(8085)=2018
�ł��邩��C���߂�ŏ��̐����� n �́Cn=8085 (��)
���2�F
��蕶�ŗ^�����Ă��铙���̍��ӂ́C71������D
������71���́Cfloor(x) �܂��� floor(x+1) �̂����ꂩ�ɓ������D
71*28 �� 2018 ��71*29
�ł��邱�Ƃ��l����Cfloor(x)=28 �ł���D
2018
=71*28 + 30
=71*floor(x) + 30
=41*floor(x) + 30*(floor(x)+1)
�ł��邩��C71���̂����C�͂��߂�41���� floor(x) �ł���C
�c���30���� floor(x)+1 �ł���D
���������āC
floor(x+59/100)=28 ���@floor(x+60/100)=29
�ƂȂ�D
����āC
28+40/100 �� x �� 28+41/100
�ł���D
����āC2840 �� 100*x �� 2841 �ł��邩��C
floor(100*x)=2840 (��)
���3�F
���̐����̂����C�O�i�@�ŕ\�����Ƃ��C���̕\�L�� 0 �� 1 �̍��X
2��ނ̐�����������Ȃ��悤�Ȃ��̂̏W���� S �Ƃ���D
S�̌������������ɕ��ׂ����̂���蕶�ɗ^�����Ă��鐔��ł���D
(1)
355���i�@�ŕ\���ƁC101100011 �ł���D
�O�i�@�ŕ\���ꂽ 101100011 ���\�i�@�ŕ\���ƁC7537�D
���̐����355�Ԗڂ̍��� 7537 (��)�D
(2)
355���O�i�@�ŕ\���ƁC111011�D
��i�@�ŕ\���ꂽ 111011 ���\�i�@�ŕ\���ƁC59�D
355�͂��̐���̑�59�Ԗ�(��)�Ɍ����D�@
(3)
S�̔C�ӂ̌� x �́C
x=��[k=0,n] a[k]*3^k (n �͐������C�ea[i]�� 0 �܂��� 1)
�Ƃ����`�ɂ�����D
x=��[k=0,n] a[k]*3^k
=a[0]+��[k=1,n] a[k]*3^k
=a[0]+3*��[k=1,n] a[k]*3^(k-1)
�ƕό`�ł��邩��Cx��3�Ŋ���Ɨ]��� 0 �܂��� 1 �̂����ꂩ�ł���D
2018��3�Ŋ���Ɨ]��� 2 �ł��邩��C2018��S�̌��ł͂Ȃ��D
�����2018�͂��̐���Ɍ���Ȃ��D
���3 (3) �Ɋւ��Ăł����C������ N ��C�ӂɗ^�����Ƃ��CN�����̐���
�Ɍ���邩�ǂ����肷����@�́C�͂����Ă���̂ł��傤���H
�����̗���FN���R�i�@�ŕ\�����Ƃ��A�ʂɂQ���P�ł���������A���̐���ɂ͂łĂ��܂���B
�F����ŁA���ɗǂ����@����������Ă��������B��
�u�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B