�����R�O�N�Q���P�W��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��356�����w�I�ȉ����
�@�@�@�@����W���ԁF1��21���`2��18����
�m���ʊ�2��n
�@
�ߋ��̐��w�I�����s�b�N�̖��ł��B�ꕔ���肵�Ă���܂��B
���P�@
�R�ӂ̒��������ꂼ��`�a���V�C�a�b���U�C�`�b���T�̎O�p�`�`�a�b�̕ӂa�b��ɓ_�o���Ƃ�A�o���Q�ӂ`�a�A�`�b�։��낵�������̑������ꂼ��l�C�m�Ƃ���B�l�C�m�Ԃ̋������ŏ��ɂ���悤�Ȃo�̈ʒu���o�O�Ƃ����Ƃ��a�o�O�̒��������߂�B�܂��A���̂Ƃ��̂l�C�m�Ԃ̋��������߂�B
���Q
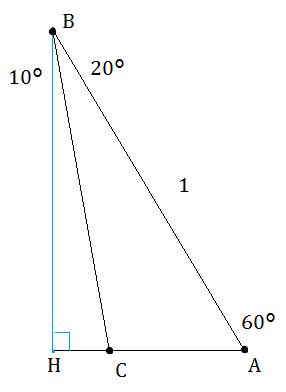
�@�O�p�`�`�a�b�Łڂ`���U�O���A�ڂa���Q�O���A�`�a���P�̂Ƃ��A
(�P�^�`�b)�|�a�b�̒l�����߂�B
�@
NO1�u���N���̂�������v 01/23 14��42���@��M �X�V 2/18
356�@���N���̂�������
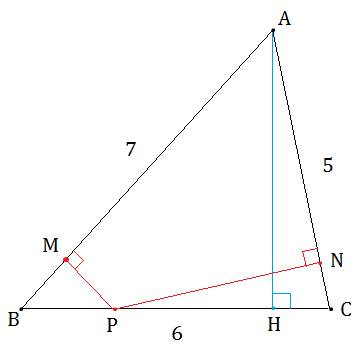
���1
�܂��A�}�̂悤�ɁA���_A����BC�ɐ���AH�������܂��B
�O�����̒藝���AAH�ɂ��āA
![]() ���A
���A![]()
![]() ���A
���A![]()
����āA
![]()
![]()
![]()
![]()
�ȏォ��A
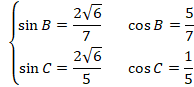
�����ŁABP��t �ƒu���ƁA
![]()
![]()
��AMPN�́A�����������p�̘a��180���Ȃ̂ŁA��PMN�ɂ��āA�]���藝����A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
����āAt��5�̂Ƃ��AMN�͍ŏ��l���Ƃ�܂��B
P0�̈ʒu�́AA����BC�ւ̐����̑���H�Ɠ����Ƃ���ł��B
BP0��5
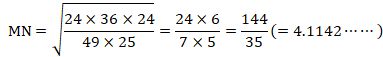
���2
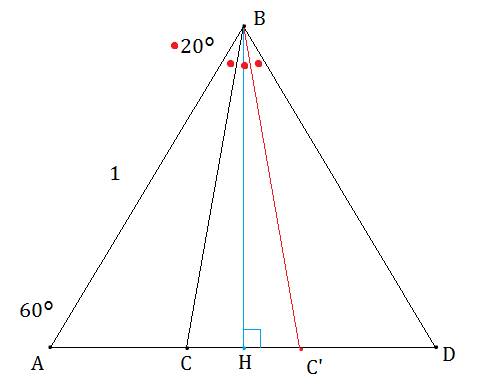 ��ABD�͐��O�p�`�ł��B
��ABD�͐��O�p�`�ł��B
��ABD��3��������2�_���AC�AC�f �Ƃ��܂��B
��ABC�f �ɒ����藝�i�p�b�v�X�̒藝�j��p����ƁA
![]()
![]()
![]()
![]()
�S�̂�AC�Ŋ���ƁA
![]()
�u���N���̂�������v 01/25 18��22���@��M
�X�V 2/18
356�Q2�@���N���̂�������
 ���1
���1
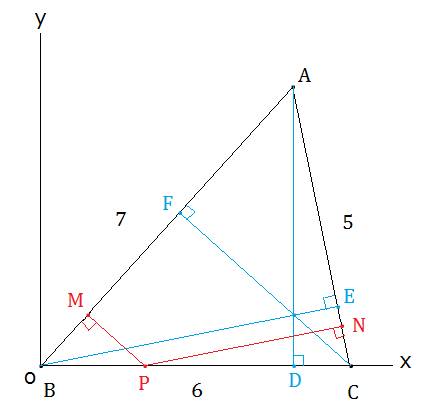
�}�̂悤�ɁAXY���W���ʓ��ɁA��ABC��u���܂��B
���_A��![]() �A���_B��
�A���_B��![]() �A���_C��
�A���_C��![]() �ł��B
�ł��B
�܂��A�e���_A�AB�AC����Εӂւ̐����̑����AD�AE�AF�Ƃ��܂��B
�i�O�̐�����1�_�Ō����܂��j
��̉��A
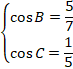
�_D�̍��W��![]()
����āA�x�N�g��![]() �́A
�́A
![]()
�܂��A�x�N�g��![]() �́A
�́A
![]()
���ɁA��BC��̓_P����}�̂悤�ɐ����������܂��B
P�̍��W��![]() �Ƃ���ƁA
�Ƃ���ƁA
��BPM�䁢BCF�Ȃ̂ŁA
![]()
�܂��A��CPN�䁢CBE�Ȃ̂ŁA
![]()
�ȏォ��A
![]()
![]()
![]()
����āA
![]()
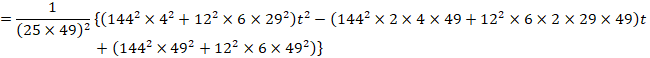
![]()
![]()
����āAt��5�̂Ƃ��AMN�͍ŏ��l���Ƃ�܂��B
P0�̈ʒu�́AA����BC�ւ̐����̑���H�Ɠ����Ƃ���ł��B
BP0��5
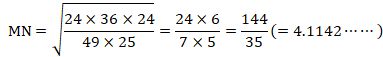
���2
�}�̂悤��AC�̉�����ɒ��_B���琂���������܂��B
![]()
![]()
 ����āA
����āA
![]()
���āA
![]()
�Ȃ̂ŁA
![]()
����āA
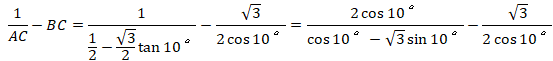
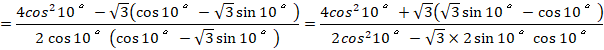
![]()
![]()
�u���N���̂�������v 02/04 06��30���@��M
�X�V 2/18
356�Q3�@���N���̂�������
���2
���}�̂悤�ɁA�ӂ̒���1�̐��O�p�`5��3�i�ɏd�˂܂��B
���_B�����ABC��20���ƂȂ�悤�Ȑ��������܂��B�iBD�j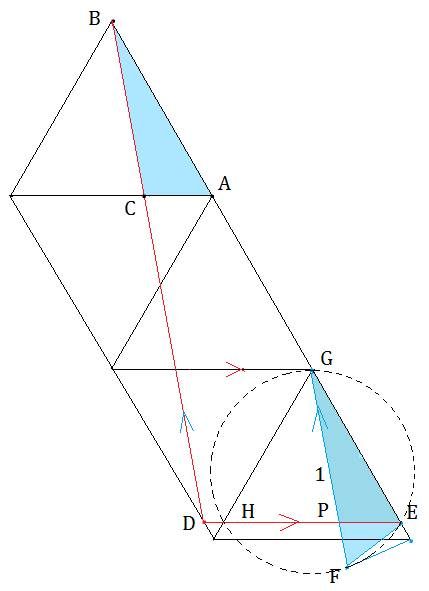
D�̂Ƃ��납���ӂɕ��s�Ȑ��������܂��B�iDE�j
����ƁA��BAC�䁢BED�ƂȂ�܂��B
BA�FAC��BE�FED
1�FAC��BE�F1
����āA
![]()
����ƁA
![]()
�y���z�ŁABC��GE�������܂��B
����ƁA
![]()
�ł��邱�Ƃ��킩��܂��B
�y���z
�����炷��
G�̂Ƃ��납��BD�ɕ��s�Ȑ�GF�������܂��B�iGF�j
���̂Ƃ�GF��1�ƂȂ�悤�ɂ��܂��B
��BAC�䁢GEP�ł��B
![]()
�Ȃ̂ŁA
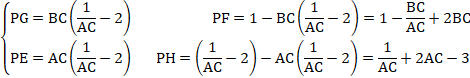
���ɁAPG�~PF��PE�~PH�ł��邱�Ƃׂ܂��B
��������A���ׂ��̒藝�̋t����A4�_E�AG�AH�AF������~����ɂ���܂��B
����ƁA��GE�ɂ��~���p�Ȃ̂Ł�EFG��60���ł��B
��������ƁA��BAC�߁�GFE�ƂȂ�ABC��GE�ł��B
��PG�~PF��PE�~PH�̌v�Z��
�r���A���낢��Ȍ������g���܂��B
�y�����z
![]()
![]()
![]()
![]()
��ABC�ɐ����藝���g���܂��B�i�P�ʂ́u���v�͏ȗ����܂��j
![]()
���A
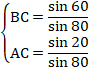
PG�~PF��PE�~PH�ł��邱�Ƃ������̂ɁA��ׂ܂��B
�r���Ȃ�ׂ��Ă����܂��B
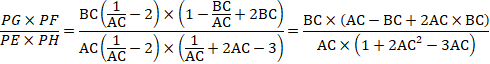
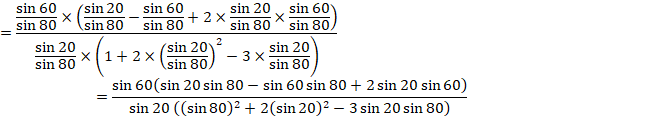
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
�����ŕ���ƕ��q�̎������قȂ邱�ƂɋC�Â��܂��B
�����ŁA���q�ƕ���̍��ׂ܂��B
![]()
![]()
![]()
![]()
![]()
![]()
�����ŁA���J�b�R�̒��́A
![]()
![]()
![]()
![]()
�ƂȂ�A���q�ƕ��ꂪ���������Ƃ��킩��܂��B
PG�~PF��PE�~PH����������̂ŁA���ׂ��̒藝�̋t����A4�_E�AG�AH�AF������~����ɂ���܂��B
NO2�uKasama�v
02/03 18��31���@��M �X�V 2/18
|
���P |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
���Q |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
NO3�u��x�Ђ����v 02/04
12��16���@��M �X�V 2/16
[��� 1]
�l�p�`AMPN �ɂ����āC��M=��N=90���ł���̂ŁC
�l�p�`AMPN�͉~�ɓ��ڂ���D���̉~��D�Ƃ���D
����AP��D�̒��a�ł���D����AP�̒��_��E�Ƃ���D
�O�p�`EMN�ɗ]���藝��K�p���āC
MN^2=EM^2+EN^2-2*EM*EN*cos(��MEN) ---(��)
�����ŁC
EM=EN=EA=(1/2)*AP�C
cos(��MEN)
=cos(2*��MAN)
=2*(cos(��MAN))^2 - 1
=2*((7^2+5^2-6^2)/(2*7*5))^2 - 1
=-503/1225
�ł���̂ŁC������(��)�ɑ�����āC
MN^2=(864/1225)*AP^2�D
����āC
MN���ŏ� �� AP���ŏ�
�ł���D
A�����BC�ɉ��낵�������̑���H�Ƃ���D
AP���ŏ��ƂȂ�̂́CP��H�Ɉ�v����Ƃ��ł���D
AB^2-BH^2=AC^2-(6-BH)^2 ���C
BH=(AB^2-AC^2+36)/12=5�D
�܂��CAH^2=AB^2-BH^2=24�D
�ȏ���C< br>BP_0 = BH = 5 (��)
MN�̍ŏ��l�́C(864/1225)^(1/2)*AH = 144/35 (��)
[��� 2]
����AB��ɁC��ADC=60���ƂȂ�悤�� �_ D ���Ƃ�D
�pDCB�̓����Ɛ���AB�Ƃ̌�_��E�Ƃ���D
����CE��ɁC��CDF=60���ƂȂ�悤�� �_ F ���Ƃ�D
�O�p�`ADC�͐��O�p�`�ł���D
DE�FBE = DC�FBC �ł��邩��C
BE=(DE*BC)/DC=(DE*BC)/AC ---(1)
�܂��CDE+BE=DB=AB-AD=1-AC ---(2)
(1)�C(2)���C
DE=AC*(1-AC)/(AC+BC) ---(3)
����āC
AE=AD+DE=AC+AC*(1-AC)/(AC+BC)=AC*(1+BC)/(AC+BC) ---(4)
��DCF=��ABC=20���C��CDF=��BAC=60���ł���̂ŁC
��ABC �� ��DCF�D
����āC
AB�FAC = DC�FDF�D
����āC
DF=(AC*DC)/AB=AC^2 ---(5)
��AEC �� ��DEF �ł�w)���C�E�@���E�d�FAC = DE�FDF�D
����āCAC*DE = AE*DF ---(6)
(3),(4),(5)��(6)�ɑ�����āC
AC*(AC*(1-AC)/(AC+BC)) = (AC*(1+BC)/(AC+BC))*(AC^2)�D
����āC
BC=(1/(AC))-2�D
����āC(1/(AC))-BC = 2 (��)
NO4�u�l�c�����v �@�@02/15 13��13���@��M �X�V 2/18 �@
���P
�@�@cos�`��(�`�a�Q�{�`�b�Q�|�a�b�Q)�^(�Q�E�`�a�E�a�b)
�@�@�@�@�@��(�V�Q�{�T�Q�|�U�Q)�^(�Q�E�V�E�T)���P�X�^�R�T
�@�@cos�a��(�`�a�Q�{�a�b�Q�|�`�b�Q)�^(�Q�E�`�a�E�`�b)
�@�@�@�@�@��(�V�Q�{�U�Q�|�T�Q)�^(�Q�E�V�E�U)���T�^�V
�@�@cos�b��(�a�b�Q�{�`�b�Q�|�`�a�Q)�^(�Q�E�a�b�E�`�b)
�@�@�@�@�@��(�U�Q�{�T�Q�|�V�Q)�^(�Q�E�U�E�T)���P�^�T
�@�a�o�����i�O�������U�j�Ƃ���ƁC
�@�@�a�l���a�ocos�a���T�^�V�E���� �@�@�b�m���b�ocos�b���P�^�T�E(�U�|��)
�@�@���`�l���`�a�|�a�l���V�|�T�^�V�E����(�S�X�|�T��)�^�V�C
�@�@�@�`�m���`�b�|�b�m���T�|�P�^�T�E(�U�|��)��(�P�X�{��)�^�T
�@���`�l�m�ɂ����āC
�@�@�l�m�Q���`�l�Q�{�`�m�Q�|�Q�E�`�l�E�`�m�Ecos�`
�@�@�@�@�@��(�S�X�|�T��)�Q�^�V�Q�{(�P�X�{��)�Q�^�T�Q�|�Q�E(�S�X�|�T��)�^�V�E(�P�X�{��)�^�T�E�P�X�^�R�T
�@�@���R�T�Q�l�m�Q���Q�T(�S�X�|�T��)�Q�{�S�X(�P�X�{��)�Q�|�R�W(�S�X�|�T��)(�P�X�{��)
�@�@�@�@�@�@�@�@�@���U�O�O�Q�T�|�P�Q�Q�T�O���{�U�Q�T���Q�{�P�V�U�W�X�{�P�W�U�Q���{�S�X���Q�|�R�T�R�V�W�{�P�V�S�W���{�P�X�O���Q
�@�@�@�@�@�@�@�@�@���W�U�S���Q�|�W�U�S�O���{�S�Q�R�R�U
�@�@�@�@�@�@�@�@�@���W�U�S(���|�T)�Q�{�Q�O�V�R�U
�@�O�������U���C�l�m���ŏ��ƂȂ�Ƃ��C�����T�ł���C�l�m�̍ŏ��l�́C
�@�@(�Q�O�V�R�U�^�R�T�Q)�P�^�Q���P�S�S�^�R�T
�@�̂ɂa�o�O���T�ł���C�l�m�̍ŏ��l�͂P�S�S�^�R�T�ł���D
���Q
�@�����藝���C
�@�@�a�b�^sin�`���b�`�^sin�a���`�a�^sin�b
�@�@���a�b�^sin�U�O�����`�b�^sin�Q�O�����P�^sin(�P�W�O���|�U�O���|�Q�O��)
�@�@���a�b��sin�U�O���^sin�P�O�O�������R�^(�Qsin�W�O��)�����R�^(�Qcos�P�O��)�C
�@�@�@�`�b��sin�Q�O���^sin�P�O�O����(�Qsin�P�O��cos�P�O��)�^cos�P�O�����Qsin�P�O��
�@�@���P�^�`�b�|�a�b���P�^(�Qsin�P�O��)�|���R�^(�Qcos�P�O��)
�@�@�@�@�@�@�@�@�@�@��(cos�P�O���|���Rsin�P�O��)�^(�Qsin�P�O��cos�P�O��)
�@�@�@�@�@�@�@�@�@�@��{�Q(cos�P�O���E�P�^�Q�|sin�P�O���E���R�^�Q)}�^sin�Q�O��
�@�@�@�@�@�@�@�@�@�@���Q�E(cos�P�O���Ecos�U�O���|sin�P�O���Esin�U�O��)�^sin�Q�O��
�@�@�@�@�@�@�@�@�@�@���Q�Ecos(�P�O���{�U�O��)�^sin�Q�O��
�@�@�@�@�@�@�@�@�@�@���Q�Ecos�V�O���^sin�Q�O��
�@�@�@�@�@�@�@�@�@�@���Q�Esin�Q�O���^sin�Q�O��
�@�@�@�@�@�@�@�@�@�@���Q�E�E�E�i���j
