平成30年7月8日日
 [流れ星]
[流れ星]
第361回数学的な応募解答
<解答募集期間:6月10日~7月8日>
[条件付き不等式]
最近購入した本に「競技数学アスリートをめざそう 国際数学オリンピックへの道標」があります。その中にあった問題です。

チェビシェフの不等式はこのサイトをご覧ください。
参考:問題1は1996年スロベニアからの候補問題
問題2は2000年アメリカからの出題
問題3は1998年ロシアからの候補問題
NO1「二度漬け白菜」 06/16 ??時??分 受信
更新 7/8
<水の流れ:こちらの不手際で、受信時間は不明です。申し訳ありません>
[問題 1]
(証明)
a^5+b^5
=(a+b)*(a^4-a^3*b+a^2*b^2-a*b^3+b^4)
=(a+b)*(a^2*b^2+(a-b)^2*(a^2+b^2+a*b))
≧(a+b)*a^2*b^2.
よって,
a^5+b^5+a*b≧(a+b)*a^2*b^2+a*b.
よって,
a*b/(a^5+b^5+a*b)
≦a*b/((a+b)*a^2*b^2+a*b)
=a*b*c^2/((a+b)*a^2*b^2*c^2+a*b*c^2)
=c/(a+b+c).
つまり,
a*b/(a^5+b^5+a*b)≦c/(a+b+c) ---(1)
同様にして,
b*c/(b^5+c^5+b*c)≦a/(a+b+c) ---(2)
c*a/(c^5+a^5+c*a)≦b/(a+b+c) ---(3)
を得る.
(1),(2),(3) の辺々を加えて,
a*b/(a^5+b^5+a*b)+b*c/(b^5+c^5+b*c)+c*a/(c^5+a^5+c*a)≦1.
よって,問題文の不等式が証明できた.
等号成立は a=b=c=1 のときのみ.
(終)
[問題 2]
(証明)
正の実数 x,y に対して,
F(x,y)=x-1+1/y
とする.
問題文の不等式は,
F(a,b)*F(b,c)*F(c,a)≦1 ---(★)
である.
次の3つの等式 (1),(2),(3)が成り立っていることが
容易に確認できる.
2=(1/a)*F(a,b)+c*F(b,c) ---(1)
2=(1/b)*F(b,c)+a*F(c,a) ---(2)
2=(1/c)*F(c,a)+b*F(a,b) ---(3)
F(a,b)≦0 の場合を考えてみる.
このとき,(1),(3)より,F(b,c)>0,F(c,a)>0
であることがわかる.
よって,F(a,b)≦0 のときには,
F(a,b)*F(b,c)*F(c,a)≦0
となるので,(★)が成り立つ.
同様にして,F(b,c)≦0,F(c,a)≦0 の各々の
場合にも,やはり(★)が成り立つことが示せる.
次に, F(a,b)>0 かつ F(b,c)>0 かつ F(c,a)>0
の場合を考える.
(1),(2),(3) の辺々を加えて,さらに
(相加平均)≧(相乗平均) を用いると,
6=(1/a)*F(a,b)+c*F(b,c)+(1/b)*F(b,c)+a*F(c,a)+(1/c)*F(c,a)+b*F(a,b)
≧6*((1/a)*F(a,b)*c*F(b,c)*(1/b)*F(b,c)*a*F(c,a)*(1/c)*F(c,a)+b*F(a,b))^(1/6)
=6*(F(a,b)*F(b,c)*F(c,a))^(1/3).
よって,1≧(F(a,b)*F(b,c)*F(c,a))^(1/3).
よって,F(a,b)*F(b,c)*F(c,a)≦1.
よって この場合にも(★)は成り立つ.
以上により,不等式(★)が証明できた.
(★)において等号が成立するのは,
a=b=c=1 のときのみ.
(終)
[問題 3]
(証明)
3個の正項
a^3/((1+b)*(1+c)),(1+b)/8,(1+c)/8,
に対して, (相加平均)≧(相乗平均) を用いると,
a^3/((1+b)*(1+c))+(1+b)/8+(1+c)/8
≧3*((a^3/((1+b)*(1+c))*((1+b)/8)*((1+c)/8))^(1/3)
=(3/4)*a.
よって,
a^3/((1+b)*(1+c))≧(3/4)*a-(b+c)/8-1/4 ---(1)
同様にして,
b^3/((1+c)*(1+a))≧(3/4)*b-(c+a)/8-1/4 ---(2)
c^3/((1+a)*(1+b))≧(3/4)*c-(a+b)/8-1/4 ---(3)
を得る.
(1),(2),(3) の辺々を加えて,
a^3/((1+b)*(1+c))+b^3/((1+c)*(1+a))+c^3/((1+a)*(1+b))
≧(1/2)*(a+b+c)-3/4
≧(1/2)*3*(a*b*c)^(1/3)-3/4
=3/4.
つまり,
a^3/((1+b)*(1+c))+b^3/((1+c)*(1+a))+c^3/((1+a)*(1+b))≧3/4.
よって,問題文の不等式が証明できた.
等号成立は a=b=c=1 のときのみである.
(終)
-------------------------------------------------
[問題 1] について:
この問題を一般化した,次の事柄が成り立ちます.
a*b*c=1 をみたすような正の実数 a,b,c と,
任意の正整数 n に対して,次の不等式が成り立つ.
(a^n*b^n)/(a^(2*n+3)+b^(2*n+3)+a^n*b^n)+
(b^n*c^n)/(b^(2*n+3)+c^(2*n+3)+b^n*c^n)+
(c^n*a^n)/(c^(2*n+3)+a^(2*n+3)+c^n*a^n)≦1.
(証明)
Muirhead の不等式により,
a^(2*n+3)+b^(2*n+3)≧a^(n+2)*b^(n+1)+a^(n+1)*b^(n+2)
が成り立つ.
よって,
(a^n*b^n)/(a^(2*n+3)+b^(2*n+3)+a^n*b^n)
≦(a^n*b^n)/(a^(n+2)*b^(n+1)+a^(n+1)*b^(n+2)+a^n*b^n)
=(a^n*b^n)/((a+b)*(a^(n+1)*b^(n+1))+a^n*b^n)
=(a^n*b^n*c^(n+1))/((a+b)*(a^(n+1)*b^(n+1)*c^(n+1))+a^n*b^n*c^(n+1))
=c/(a+b+c).
よって,
Σ[cyc](a^n*b^n)/(a^(2*n+3)+b^(2*n+3)+a^n*b^n)
≦Σ[cyc]c/(a+b+c)
=1.
(証明終)
Muirhead の不等式については,ここに詳しい解説があります.
https://www.math.ust.hk/excalibur/v11_n1_20161130.pdf
(以上)
NO2「早起きのおじさん」
06/22 21時06分 受信 更新 7/8
<コメント:問題のヒントをはじめ考えましたが、今一つよくわからなかったので、関係なく好きに解きました。
問題2は、a、b、cの置き方を解答の逆数にすれば、1ステップ少なくて済むと気づきましたが、本質的でないと思ったので、思いついた通りの解答にします。>
問題1
![]()
![]() なので、
なので、
![]()
![]()
分母を払って、右辺から左辺を引くと、
![]()
![]()
![]()
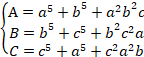
とおくと、

なので、
![]()
![]()
![]()
![]()

なので、式(1)は、
![]()
となり、この式を考えます。
このままでは、うまくいかないので、工夫をします。
![]()
![]()
![]()
先ず、前半部分は、
![]()
![]()
![]()
![]()
![]()
次に、後半部分は、
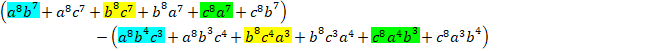
![]()
![]()
![]()
![]()
以上から、式(2)は成り立ちます。
よって、式(1)も成り立ち、元の式も成り立ちます。
等号の成立は、
![]()
から、![]() のときです。
のときです。
問題2
![]()
![]() なので、
なので、![]() とおきます。
とおきます。
![]() です。
です。
![]()
![]()
分母を払って、
![]()
ここで、![]() とおきます。
とおきます。
![]()
右辺から左辺を引いた、
![]()
この式で、考えることにします。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ここで ![]() は正の三実数で、
は正の三実数で、![]() としても問題ありません。
としても問題ありません。
式(5)の初めの項は、負になりません。
2重下線の部分は、正と非負と非負の積なので、負になりません。
よって、式(3)は成立します。
等号の成立は、式(4)から、![]() より、
より、![]() のときです。
のときです。
![]() なので、
なので、![]() になります。
になります。
つまり、![]() です。
です。
問題3
相加平均と相乗平均の関係と![]() より、
より、
![]()
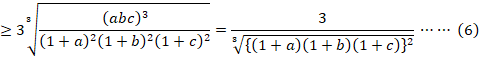
等号の成立は、
![]()
のときです。
前半部分から、
![]()
![]()
![]()
![]()
![]()
より、![]() のときです。
のときです。
同様に、後半部分から、![]() のときです。
のときです。
つまり、![]() のときです。
のときです。
これを式(6)に入れると、
![]()
以上から示すことができました。
NO3「Kasama」
06/30
18時32分 受信 更新 7/8
問題1
ヒントを参考して、
![]()
とイメージしておきます。
与式の各項は巡回的なので、第1項で導いた結果を、他の項に適用すればよいです。
すると、
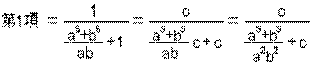
なので、これを①式の第1項に関連付けるには、
![]()
となれば都合が良いです。それを示すため、左辺から右辺を引いて変形すると、

です。よって、
![]()
です。第2、3項についても同様ですから、
![]()
となり、与式は成り立ちます(等号はa=b=c=1の場合)。
問題2
abc=1なので、
a=y/z、b=z/x、c=x/y (x>0、y>0、z>0)
とおいて、与式の左辺を書き換えると、
![]()
です。与式の右辺は1なので、
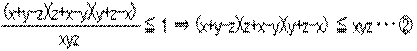
を示せばよいです。
x、y、zは巡回的なので、x≦y≦zとしても一般性を失いません。すると、z+x-y≧0、y+z-x≧0ですから、x+y-zの符号で場合分けして考えます。
(1)x+y-z<0の場合
左辺<0なので、②式は成り立ちます。
(2)x+y-z≧0の場合
相加・相乗平均の関係より、
![]()
![]()
![]()
③④⑤を掛け合わせると、
(x+y-z)(z+x-y)(y+z-x)≦xyz
よって、②式は成り立ちます。
(1)(2)より、与式は成り立ちます(等号はa=b=c=1の場合)。
問題3
abc=1に留意して、a、b、cに相加・相乗平均の関係を適用させると、
![]()
![]()
次に、ヒントに書かれているように、チェビシェフの不等式を利用して、
与式の左辺を2つの積に分割します。

これに⑦式を当てはめると、
![]()
です。分母をそろえて、
![]()
これが3/4以上であることを示せばよいのです。
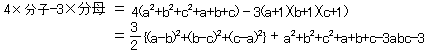
abc=1と⑥⑦式より、
![]()
ゆえに、与式は成り立ちます(等号はa=b=c=1の場合)。
<水の流れの解答>

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。
