�����R�O�N�X���Q��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��363�����w�I�ȉ����
�@�@�@�@����W���ԁF�W���T���`�X���Q����
�m�Ώ̎��̒l�n
�@
�����̗��ꂩ��A�u���N���̂�������v����8��8���ߌ�4���Ɏw�E����܂����̂ł����ɁA�������܂��B�ł��ˁB����ȃ~�X�����Đ\����܂���B��
NO1�u���N���̂�������v 08/08 16��01���@��M �X�V 9/2
���1
(1)
![]()
![]()
![]()
![]()
(2)
![]()
�܂�A
![]()
�܂�A���� ![]() �A��2��
�A��2�� ![]() �ł���t�B�{�i�b�`����ƂȂ�܂��B
�ł���t�B�{�i�b�`����ƂȂ�܂��B
363�̎���
���2 �ŁA
![]()
�Ƃ���܂����A�E�ӂ̉E�̍��́u�I�v�̋L���̈Ӗ���������܂���B
�������������B
�u���N���̂�������v 08/09 11��57���@��M �X�V 9/2
����̈�ʍ��́A�v�����Ȃ������̂ŁA���߂܂���ł����B
���1
(1)
![]()
![]()
![]()
![]()
(2)
![]()
�܂�A
![]()
�܂�A���� ![]() �A��2��
�A��2�� ![]() �ł���t�B�{�i�b�`����ƂȂ�܂��B
�ł���t�B�{�i�b�`����ƂȂ�܂��B
���2
(1)
![]()
![]()
![]()
![]()
(2)
�� ![]()
�܂�A
![]()
���ʂ̍l��
![]()
���̎��̕�����Đ�������ƁA
![]()
����́A
![]()
�Ȃ̂ŁA1�̗������̂����A�����łȂ����̂��A(*)�����܂��B
(*)�̉��́A
![]()
�Ⴆ�A![]() �Ƃ���ƁA
�Ƃ���ƁA![]() �A
�A![]()
�u�������āA![]() �Ƃ���ƁA
�Ƃ���ƁA![]() �A
�A![]()
���̐}�ŁA![]() ��
�� ![]() �Ƃ́A�����Ώ̂̈ʒu�ɂ���܂��B
�Ƃ́A�����Ώ̂̈ʒu�ɂ���܂��B
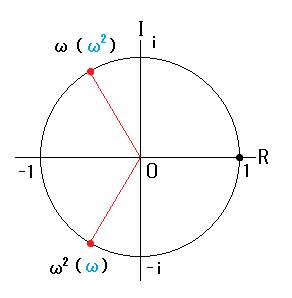
�܂��A
![]()
![]()
�܂�A![]() ��
�� ![]() �Ƃ́A�t���̊W�ɂ���܂��B
�Ƃ́A�t���̊W�ɂ���܂��B
�ȏォ��A
![]()
![]()
![]()
![]()
�܂�A
![]()
![]()
![]()
�ł��B
NO2�u�l�c�����v �@�@08/22 09��44���@��M �X�V 9/2
���P
�@���{�����P�C�������|�P�C�s���������{�����i�����P�C�Q�C�R�C�E�E�E�j
�i�P�j�s�P�����{�����P
�@�@�s�Q�����Q�{���Q��(���{��)�Q�|�Q�������P�Q�|�Q(�|�P)���R�E�E�E�i���j
�@�����ŁC
�@�@�s���{�Q�������{�Q�{�����{�Q��(�����{�P�{�����{�P)(���{��)�|����(�����{����)���s���{�P�{�s��
�@�̂ɐ���o�s���p��Fibonacci����ł���D
�@�@���s�R���s�Q�{�s�P���R�{�P���S�E�E�E�i���j
�@�@�@�s�S���s�R�{�s�Q���S�{�R���V�E�E�E�i���j
�@�@�@�s�T���s�S�{�s�R���V�{�S���P�P�E�E�E�i���j
�i�Q�j�i�P�j���C�s���{�Q���s���{�P�{�s��
�@�@�s���{�Q�|���s���{�P����(�s���{�P�|���s��)�E�E�E(1)
�Ƃ���ƁC
�@�@�s���{�Q��(���{��)�s���{�P�|�����s�����s���{�P�{�s��
�@�@�����{�����P�C�������|�P
�@�̂Ƀ��C���́C�Q�����������Q�|���|�P���O�̂Q���ł���D
�@����(�P�|��T)�^�Q�C����(�P�{��T)�^�Q�Ƃ���D
�@(1)���C����o�s���{�P�|���s���p�C�o�s���{�P�|���s���p�́C���ꂼ�������C���̓��䐔��ł���D
�@�@���s���{�P�|���s����(�s�Q�|���s�P)�����|�P��(�R�|��)�����|�P��(�Q�{��)�����|�P�C
�@�@�@�s���{�P�|���s����(�s�Q�|���s�P)�����|�P��(�R�|��)�����|�P��(�Q�{��)�����|�P
�@�����ŁC
�@�@�Q�{����(�T�|��T)�^�Q���|��T�E(�P�|��T)�^�Q���|��T�E��
�@�@�Q�{����(�T�{��T)�^�Q����T�E(�P�{��T)�^�Q����T�E��
�@�@���s���{�P�|���s������T�E�����C�s���{�P�|���s�����|��T�E����
�@�ӁX�������ƁC
�@�@(���|��)�s������T�E(�����{����)
�@�@���s���������{������{(�P�{��T)�^�Q}���{{(�P�|��T)�^�Q}���E�E�E�i���j
���Q
�@���{�P�^�����|�P�C�s���������{�P�^�����i�����P�C�Q�C�R�C�E�E�E�j
�i�P�j�s�P�����{�P�^�����|�P
�@�@�s�Q�����Q�{�P�^���Q��(���{�P�^��)�Q�|�Q��(�|�P)�Q�|�Q���|�P�E�E�E�i���j
�@�����ŁC
�@�@�s���{�Q�������{�Q�{�P�^�����{�Q��(�����{�P�{�P�^�����{�P)(���{�P�^��)�|(�����{�P�^����)���|�s���{�P�|�s��
�@�@���s�R���|�s�Q�|�s�P���|(�|�P)�|(�|�P)���Q�E�E�E�i���j
�@�@�@�s�S���|�s�R�|�s�Q���|�Q�|(�|�P)���|�P�E�E�E�i���j
�@�@�@�s�T���|�s�S�|�s�R���|(�|�P)�|�Q���|�P�E�E�E�i���j
�i�Q�j���{�P�^�����|�P����C���Q�{���{�P���O
�@�@������(�|�P�}��R��)�^�Q
�@�@�@�@��cos(�}�Q�^�R)�{��sin(�}�Q�^�R)�i���������j
�@�@���s���������{���|��
�@��{cos(�Q���^�R)�{��sin(�Q���^�R)}�{{cos(�|�Q���^�R)�{��sin(�|�Q���^�R)}�C
�@{cos(�|�Q���^�R)�{��sin(�|�Q���^�R)}�{{cos(�Q���^�R)�{��sin(�Q���^�R)}
�@�@���s�����Qcos(�Q���^�R)
�@���𐮐��Ƃ���D
i). �����R���̂Ƃ��C
�@�@�s�R�����Qcos(�Q����)���Q
ii). �����R���{�P�̂Ƃ��C
�@�@�s�R���{�P���Qcos(�Q���{�Q�^�R)���|�P
iii). �����R���{�Q�̂Ƃ��C
�@�@�s�R���{�Q���Qcos(�Q���{�S�^�R)���|�P
�@�܂Ƃ߂�ƁC�����R�̔{���̂Ƃ��C�s�����Q�C����ȊO�̂Ƃ��C�s�����|�P
NO3�u�ɂ���Z12�v�@�@�@08/25 02��10���@��M �X�V 9/2
���P
�@�@��+����1�@�@�E�E�E�@
������-1�@�@�E�E�E�A
�@�@
�@�@���̎���T����xn+yn�����߂�
�@ ,�A����x2-x-1=0�E�E�E�B
�����i1�}��5�j/2
�Ώێ��Ȃ̂�
�����i1�}��5�j/2�@�i�����t���F�������̎�y�����j
�@�����A���Ƃ��͇B���̉����A���ƂȂ�܂�
T2��x2+y2
�@��((1+��5)/2)2+((1-��5)/2)2��3
T3��x3+y3
�@��((1+��5)/2)3+((1-��5)/2)3��4
T4��x4+y4
�@��((1+��5)/2)4+((1-��5)/2)4��7
T5��x5+y5
�@��((1+��5)/2)5+((1-��5)/2)5��11
�ȏ��2���W�J�Ŋm�F�ł��܂�
���݂�
T0��x0+y0
�@��2
T1��x1+y1
�@��((1+��5)/2) +((1-��5)/2)��1
�@�ƂȂ�܂��B����炩��킩��̂�
�@Tn��Tn-1+ Tn-2
�@�����lT0��2�@,T1��1
�Ƃ����K�����ł�
T�𐔗�ƌ����Ƃ�
�̐��W��������
x 2 - P x + Q =0�iP=1�AQ=-1�j
�@�̉����A���̃�n+��n�E�E�E�C
�ƂȂ��Ă��܂��B
���̖��́A�����ԈȑO�Ƀ����J����Ƃ��Đ搶����o�肳�ꂽ���Ƃ��������̂ňȑO�����U�炵��������T���čl���܂����B
�C�̓����J��������̈�ʍ��ɂȂ�܂�����ʍ���
��n-��n/��-���@�̓t�B�{�i�b�`����ƂȂ菉���l���قȂ邾���ł��ˁB
���2
�@�@��+1/x��-1�@�@�E�E�E�D
�@�@
�@�@���̎���T����xn+1/xn�����߂�
�@�D��
�@�@x 2+x+1=0�ƕό`�ł��܂��B�����
�̐��W��������
x 2 - P x + Q =0�iP=-1�AQ=1�j
�ƌ������ł����̉���
����(�|1�{��3��)/2=cos2/3�� +isin2/3�� �E�E�E�E
����(�|1�|��3��)/2=cos -2/3��+isin-2/3�E�E�E�F
�i�E�ƇF�͕��f���ʂ̒P�ʉ~��ŋ���) �E�E�E�G
�@�@��1/�������ƒu���ƇD��
�@�@�@��+����-1
�@�@�@�������P
�@�@�@�Ə����܂����AT����xn+yn�Ȃ̂Ŗ��P�Ɠ����ݖ�ƂȂ��Ă��܂��iP=-1�AQ=1�Ɩ��P�Ƃ͌W�����t�ɂȂ��Ă��܂����j�B
�@�@�@����Ă�������������J����ƂȂ�܂��B
�@�@�@�@���������J����̒�`��
�@ Tn=PTn-1-QTn-2�E�E�E�H
�@�@�@�@�@���|�iTn-1+Tn-2)�E�E�E�I
�@�����ŏ����Q�������߂��
�@�@�@T0��x0+y0��2
�@�@�@T1��x1+y1��-1��P�i�D�Ɠ��`�j
�܂��H�I����
�@�@�@T2��x2+y2��(-1)�E(-1) �|1�E(2)=-1
�@�@�@T3��x3+y3��(-1)�E(-1) �|1�E(-1)=2
�@�@�@T4��x4+y4��(-1)�E(2) �|1�E(-1)=-1
�@�@�@T5��x5+y5��(-1)�E(-1) �|1�E(2)=-1
�@�@�@T6��x6+y6��(-1)�E(-1) �|1�E(-1)=2
�@�@�@T7��x7+y7��(-1)�E(2) �|1�E(-1)=-1
�@�@�@T8��x8+y8��(-1)�E(2) �|1�E(-1)=-1
�ƂȂ�A�O�Q���̘a��-1���|�������̂����̍��ɂȂ�܂�
�@�@�@T0��2
�@�@�@T1��-1
Tn��-(Tn-1+
Tn-2)
�����ł�2�A-1�A-1���J��Ԃ�����ƂȂ�܂��E�E�E�E�E�E�E�E�E�E�E�E��
���̂��Ƃ��A�E�F�G����l���Ă݂܂����B�h���A�u���̒藝����
��n��(cos2/3�� +isin2/3��)n=(cos2/3n�� +isin2/3n��) �E�E�E�J
��n��(cos -2/3��+isin-2/3��)n=(cos-2/3n��+isin-2/3n��)�E�E�E�K
�J�{�K��n���R�̔{���i�O���܂ށj�̎�������Ɉ�v���Ƃ���1�ƂȂ邽�ߘa��2�ƂȂ�R�̔{���ł͂Ȃ��ꍇ
�݂��ɋ����Ȃ��ߋ����̓L�������A�E�g��������͂Ƃ���-1/2�ƂȂ邽�ߘa��-1�ƂȂ�܂��B
����āA���̐����
2�A-1�A-1�A2�A-1�A-1�A2�A-1�A-1�E�E�E�E�ƂȂ�܂��B�������Ȃ��炱�̍l�����ł͑Q�����I�Ȕ��z�͕����т܂���B�i���������f���ʏ����]���鐔��͔����������܂��j
�@�@�@�@�֑�
�@�@�@�@�@P=1�AQ=-1
�@�@�@�@�@P=-1�AQ=1
�@�@�@�@�@���o�Ă��܂����̂�
�@�@�@�@�@P=-1�AQ=-1
�@�@�@�@�@P=1�AQ=1
�@�@�@�@�@�̓��������J����ɂ��������킫�܂����B
�@�@�@�@�@�悸�AP=-1�AQ=-1�ɂ��čl���܂�
�@�@�@�@�@x 2+x-1=0
�̉����A�������߂��
�@�@�@�@�@�@����(-1+��5)/2
�@�@�@�@�@�@����(-1-��5)/2
�@�@�@�@�@�@���������J����̈�ʍ���
Tn=((-1+��5)/2)n+((-1-��5)/2)n
T0����0+��0��2
T1����1+��1��-1
T2����2+��2����(-1)�E(-1) �|(-1)�E(2)=3
T3����3+��3����(-1)�E(3) �|(-1)�E(-1)=-4
T4����4+��4����(-1)�E(-4) �|(-1)�E(3)=7
Tn����n+��n��-Tn-1+Tn-2
�iTn�̐�Βl�͑O�Q���̐�Βl�̘a�ɓ������j
�@�@�@�@�@���ɁAP=1�AQ=1�ɂ��čl���܂�
�@�@�@�@�@x 2-x+1=0
�̉����A�������߂��
�@�@�@�@�@�@����(1+��3i)/2=cos1/3�� +isin1/3��
�@�@�@�@�@�@����(1-��3i)/2=cos1/3�� +isin-1/3��
�@�@�@�@�@�@���������J����̈�ʍ���
Tn=((1+��3i)/2)n+((1-��3i)/2)n
T0����0+��0��2
T1����1+��1��1
T2����2+��2����(1)�E(1) �|(1)�E(2)=-1
T3����3+��3����(1)�E(-1) �|(1)�E(1)=-2
T4����4+��4����(1)�E(-2) �|(1)�E(-1)=-1
T5����5+��5����(1)�E(-1) �|(1)�E(-2)=1
T6����6+��6����(1)�E(1) �|(1)�E(-1)=2
T7����7+��7����(1)�E(2) �|(1)�E(1)=1
T8����8+��8����(1)�E(1) �|(1)�E(2)=-1
T9����9+��9����(1)�E(-1) �|(1)�E(1)=-2
T10����10+��10����(1)�E(-2) �|(1)�E(-1)=-1
T11����11+��11����(1)�E(-1) �|(1)�E(-2)= 1
Tn����n+��n��Tn-1-Tn-2
��L�̎��͑O�q�����h���A�u���̒藝���狕���̓L�����Z������
�����́}1�A2�����Ƃ�Ȃ����Ƃ�����܂��B
�u�ɂ���Z12�v�@�@�@08/29 23��29���@��M
�X�V 9/2
���2�̉�����Ȃ������悤�ł��B���L�ɕߑ����܂���
���2
�@�@��+1/x��-1�@�@�E�E�E�D
�@�@
�@�@���̎���T����xn+1/xn�����߂�
�@�D��
�@�@x 2+x+1=0�ƕό`�ł��܂��B�����
�̐��W��������
x 2 - P x + Q =0�iP=-1�AQ=1�j
�ƌ������ł����̉���
����(�|1�{��3��)/2=cos2/3�� +isin2/3�� �E�E�E�E
����(�|1�|��3��)/2=cos -2/3��+isin-2/3�E�E�E�F
�i�E�ƇF�͕��f���ʂ̒P�ʉ~��ŋ���) �E�E�E�G
�@�@��1/�������ƒu���ƇD��
�@�@�@��+����-1
�@�@�@�������P
�@�@�@�Ə����܂����AT����xn+yn�Ȃ̂Ŗ��P�Ɠ����ݖ�ƂȂ��Ă��܂��iP=-1�AQ=1�Ɩ��P�Ƃ͌W�����t�ɂȂ��Ă��܂����j�B
�@�@�@����Ă�������������J����ƂȂ�܂��B
�@�@�@�@���������J����̒�`��
�@ Tn=PTn-1-QTn-2�E�E�E�H
�@�@�@�@�@���|�iTn-1+Tn-2)�E�E�E�I
�@�����ŏ����Q�������߂��
�@�@�@T0��x0+y0��2
�@�@�@T1��x1+y1��-1��P�i�D�Ɠ��`�j
�܂��H�I����
�@�@�@T2��x2+y2��(-1)�E(-1) �|1�E(2)=-1
�@�@�@T3��x3+y3��(-1)�E(-1) �|1�E(-1)=2
�@�@�@T4��x4+y4��(-1)�E(2) �|1�E(-1)=-1
�@�@�@T5��x5+y5��(-1)�E(-1) �|1�E(2)=-1
�@�@�@T6��x6+y6��(-1)�E(-1) �|1�E(-1)=2
�@�@�@T7��x7+y7��(-1)�E(2) �|1�E(-1)=-1
�@�@�@T8��x8+y8��(-1)�E(2) �|1�E(-1)=-1
�ƂȂ�A�O�Q���̘a��-1���|�������̂����̍��ɂȂ�܂�
�@�@�@T0��2
�@�@�@T1��-1
Tn��-(Tn-1+
Tn-2)
�@�@�@�@�@�@�@����������Ƒ�1���ŕ\����
�@�@�@T2��-(T0+T1)��-1
�@�@�@T3��T0
��2
�@�@�@T4��T1
��-1
�@�@�@T5��-(T0+T1)��-1
�@�@�@T6��T0
��2
�@�@�@T7��T1
��-1
�@�@�@T8��-(T0+T1)��-1
�@�@�@�@�@n=9,10,11��6,7,8�Ɠ����ŏz����
�����
Tn��2 (n=0(mod3))
��-1(n��0(mod3)) �E�E�E�E�E�E�E�E�E�E�E�E��
�����ł�2�A-1�A-1���J��Ԃ�����ƂȂ�܂�
���̂��Ƃ��A�E�F�G����l���Ă݂܂����B�h���A�u���̒藝����
��n��(cos2/3�� +isin2/3��)n=(cos2/3n�� +isin2/3n��) �E�E�E�J
��n��(cos -2/3��+isin-2/3��)n=(cos-2/3n��+isin-2/3n��)�E�E�E�K
�J�{�K��n���R�̔{���i�O���܂ށj�̎�������Ɉ�v���Ƃ���1�ƂȂ邽�ߘa��2�ƂȂ�R�̔{���ł͂Ȃ��ꍇ
�݂��ɋ����Ȃ��ߋ����̓L�������A�E�g��������͂Ƃ���-1/2�ƂȂ邽�ߘa��-1�ƂȂ�܂��B
����āA���̐����
2�A-1�A-1�A2�A-1�A-1�A2�A-1�A-1�E�E�E�E�ƂȂ�܂��B�������Ȃ��炱�̍l�����ł͑Q�����I�Ȕ��z�͕����т܂���B�i���������f���ʏ����]���鐔��͔����������܂��j
�@�@�@�@�֑�
�@�@�@�@�@P=1�AQ=-1
�@�@�@�@�@P=-1�AQ=1
�@�@�@�@�@���o�Ă��܂����̂�
�@�@�@�@�@P=-1�AQ=-1
�@�@�@�@�@P=1�AQ=1
�@�@�@�@�@�̓��������J����ɂ��������킫�܂����B
�@�@�@�@�@�悸�AP=-1�AQ=-1�ɂ��čl���܂�
�@�@�@�@�@x 2+x-1=0
�̉����A�������߂��
�@�@�@�@�@�@����(-1+��5)/2
�@�@�@�@�@�@����(-1-��5)/2
�@�@�@�@�@�@���������J����̈�ʍ���
Tn=((-1+��5)/2)n+((-1-��5)/2)n
T0����0+��0��2
T1����1+��1��-1
T2����2+��2����(-1)�E(-1) �|(-1)�E(2)=3
T3����3+��3����(-1)�E(3) �|(-1)�E(-1)=-4
T4����4+��4����(-1)�E(-4) �|(-1)�E(3)=7
Tn����n+��n��-Tn-1+Tn-2
�iTn�̐�Βl�͑O�Q���̐�Βl�̘a�ɓ������j
�@�@�@�@�@���ɁAP=1�AQ=1�ɂ��čl���܂�
�@�@�@�@�@x 2-x+1=0
�̉����A�������߂��
�@�@�@�@�@�@����(1+��3i)/2=cos1/3�� +isin1/3��
�@�@�@�@�@�@����(1-��3i)/2=cos1/3�� +isin-1/3��
�@�@�@�@�@�@���������J����̈�ʍ���
Tn=((1+��3i)/2)n+((1-��3i)/2)n
T0����0+��0��2
T1����1+��1��1
T2����2+��2����(1)�E(1) �|(1)�E(2)=-1
T3����3+��3����(1)�E(-1) �|(1)�E(1)=-2
T4����4+��4����(1)�E(-2) �|(1)�E(-1)=-1
T5����5+��5����(1)�E(-1) �|(1)�E(-2)=1
T6����6+��6����(1)�E(1) �|(1)�E(-1)=2
T7����7+��7����(1)�E(2) �|(1)�E(1)=1
T8����8+��8����(1)�E(1) �|(1)�E(2)=-1
T9����9+��9����(1)�E(-1) �|(1)�E(1)=-2
T10����10+��10����(1)�E(-2) �|(1)�E(-1)=-1
T11����11+��11����(1)�E(-1) �|(1)�E(-2)= 1
Tn����n+��n��Tn-1-Tn-2
��L�̎��͑O�q�����h���A�u���̒藝���狕���̓L�����Z������
�����́}1�A2�����Ƃ�Ȃ����Ƃ�����܂��B
NO4�uKasama�v
08/26 19��27���@��M �X�V 9/2
|
���P |
|
||||||||||
|
���Q |
|
NO5�u�O�p��K�v�@�@�@�@ 08/26 21��05���@��M �X�V 9/2


��������ƈꏏ�ɓo��ꂽ��ȎR�̉W���̎ʐ^�ł��B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
