�����R�O�N�P�O���Q�W��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��365�����w�I�ȉ����
�@�@�@�@����W���ԁF�X��30���`10��28����
�m���[�N���b�h�̌ݏ��@�n
�@
�P�ȏ�̂Q�̐������A���i���������͂����傫���j�ɂ��Ď��̂悤�ȑ�����s���B�������Ŋ������Ƃ��̏��������Ă����āA�]�肪������x�������̗]��Ŋ����āA�]��̂������J��Ԃ��B
�Ⴆ�A�����R�P�A�����X�W�̂Ƃ��͂����Ȃ�B
�X�W���R�P���R�A�]��͂T
�R�P���T���U�A�@�]��͂P
�T���P���T�A�]�肪�Ȃ��A����I��
�@���̂Ƃ��A�o�Ă����������ɏ����Ă݂�ƁA�R�A�U�C�T�ł���B
�����ŁA�R�P�ƂX�W�̑��݊W�͂R�C�U�A�T�ł���Ƃ����B�܂��A���݊W�ɏo�Ă��鏤�̌��i�R�P�ƂX�W�̂Ƃ��͂R�j�𑊌݊W�̒����Ƃ����B
�@�Ⴆ�A�W�ƂP�P�̑��݊W�͂P�A�Q�A�P�D�Q�ł���Ƃ����B���̒����͂S�ł���B
���P�@���݊W���P�A�Q�A�P�A�P�A�R�ƂȂ鐮���̑g���P�ȏ�100�ȉ��͈̔͂ł��ׂċ��߂Ȃ����B
���Q�@�P�ȏ�100�ȉ��͈̔͂ő��݊W���ł������Ȃ�悤�Ȑ����̑g�ׂ��Ƃ���A�������X�ł���g���ł������A������1�g��������܂���B����1�g�����߂Ȃ����B
�u�Q�l�����F�s�[�^�[�搶�ƒ��w�����̎Z���ɒ���I�v�V����
�u���N���̂�������v 10/03 21��46���@��M �X�V 10/28
��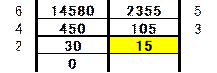 ���[�N���b�h�̌ݏ��@�́A2���̍ő�������߂���@�ł��B
���[�N���b�h�̌ݏ��@�́A2���̍ő�������߂���@�ł��B
�Ⴆ�A14580��2355�̍ő���́A���̂悤�ɋ��߂��܂��B
�܂��A2������ׂď����܂��B
�傫���������������Ŋ���܂��B�i14580����2355�́A��6�A�]��450�j
��6��14580�̍����A�]��450��14580�̉��ɏ����܂��B
�����āA����������]��Ŋ���܂��B�i2355����450�́A��5�A�]��105�j
��5��2355�̉E���A�]��105��2355�̉��ɏ����܂��B
���ɁA450��105��V����2���Ƃ��āA��Ɠ������Ƃ����܂��B
���̂悤�Ȃ��Ƃ��J��Ԃ��Ă����A�Ō�ɗ]�肪0�ƂȂ��ʂ�����܂��B
���̂Ƃ��A�����O�̗]��15���A�ŏ���2���̍ő���ƂȂ�܂��B
���łɁA2355��14580�̑��݊W�́A6,5,4,3,2�ƂȂ�A���̒����́A5�ł��B
�����[�N���b�h�̌ݏ��@�̎d�g�݂��m�F���Ă����܂��B
���E��2���̊W�́A���ɂ��鏤�Ɨ]���p���āA�\�����Ƃ��ł��܂��B
���������2���̊W�́A�E�ɂ��鏤�Ɨ]���p���āA�\�����Ƃ��ł��܂��B
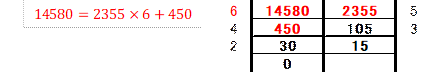
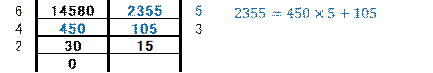
���1
���݊W���v�Z����g�̍��E�ɏ����Ă����܂��B
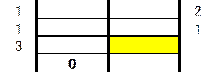
���F�̂Ƃ���ɂ́A2���̍ő��������̂ŁA1����5�̏ꍇ���v�Z���Ă݂܂��B
��̎d�g�݂��g����������2�������߂܂��B
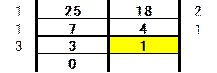


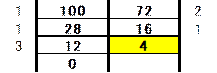

�ő����5�̂Ƃ��́A�傫������100���傫���Ȃ��Ă��܂��܂��B
����āA�����̑g�́A�i18,25�j�A�i36,50�j�A�i54,75�j�A�i72,100�j��4�ł��B
���2
 100�ȉ��Ƃ�������������̂ŁA�Ȃ�ׂ��������Ȃ�悤�ɍl���܂��B
100�ȉ��Ƃ�������������̂ŁA�Ȃ�ׂ��������Ȃ�悤�ɍl���܂��B
�ő�������������ƁA���݊W�̐������������Ƃ��l���܂��B
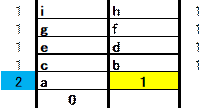
�ő����1�A���݊W��1�̕��тōŌ�̂���2�̏ꍇ���l���܂��B
���݊W�̍Ōオ1���ƁA������2�s�ڂ�1��1�ɂȂ��Ă��܂�����ł��B
�E�}�̊e���̊W���l���܂��B
�����Ō�ȊO1�Ȃ̂ŁAi=h+g�Ah=g+f�Ag=f+e�Af=e+d�Ae=d+c�Ad=c+b�Ac=b+a�Ab=a+1�A�̂悤�ɂȂ�܂��B
���ԂɑO2���̘a���A���̐��ɂȂ��Ă��܂��B
�����́A����1�A��2��2�̃t�B�{�i�b�`����ł��B
{1, 2, 3, 5, 8, 13, 21, 34, 55, 89}
�v�Z���Ă��A �ƂȂ�A�i55,89�j�����߂�g�ł��B
�ƂȂ�A�i55,89�j�����߂�g�ł��B
��������2���ɂȂ肻���ȏꍇ���l���܂��B
�����݊W�̍Ō�̐��ɂ���
�ő����1�A���݊W��1�̕��тōŌ�̂���3�̏ꍇ���l���܂��B
�v�Z����ƁA �ƂȂ�A���������܂���B
�ƂȂ�A���������܂���B
���ő�����������ꍇ
�ő����2�A���݊W��1�̕��тōŌ�̂���2�̏ꍇ���l���܂��B
�v�Z����ƁA �ƂȂ�A���������܂���B
�ƂȂ�A���������܂���B
�����݊W��1�̕��т̓r����2������ꍇ
�E8�Ԗڂ̐���2�̂Ƃ�
a�����������𐔂���ƁA
i=h+g�Ah=g+f�Ag=f+e�Af=e+d�Ae=d+c�Ad=c+b�Ac=b+a�Ab=2a+1
�@21�@ �@13 �@8�@�@�@5�@�@�@3�@�@�@2�@�@ �@1�@ �@�@1
�̂悤�ɂȂ�Ai��89+2�~21��131
�E7�Ԗڂ̐���2�̂Ƃ��A
�������������𐔂���ƁA
i=h+g�Ah=g+f�Ag=f+e�Af=e+d�Ae=d+c�Ad=c+b�Ac=2b+a�Ab=a+1
�@13 �@8�@�@�@5�@�@�@3�@�@�@2�@�@ �@1�@�@�@1
�̂悤�ɂȂ�Ai��89+3�~13��128
�E6�Ԗڂ̐���2�̂Ƃ��A
c�����������𐔂���ƁA
i=h+g�Ah=g+f�Ag=f+e�Af=e+d�Ae=d+c�Ad=2c+b�Ac=2b+a�Ab=a+1
�@8�@�@�@5�@�@�@3�@�@�@2�@�@ �@1�@�@�@1
�̂悤�ɂȂ�Ai��89+5�~8��129
�E5�Ԗڂ̐���2�̂Ƃ��A
d�����������𐔂���ƁA
i=h+g�Ah=g+f�Ag=f+e�Af=e+d�Ae=2d+c�Ad=2c+b�Ac=2b+a�Ab=a+1
�@5�@�@�@3�@�@�@2�@�@ �@1�@�@�@1
�̂悤�ɂȂ�Ai��89+8�~5��129
�E4�Ԗڂ̐���2�̂Ƃ��A
e�����������𐔂���ƁA
i=h+g�Ah=g+f�Ag=f+e�Af=2e+d�Ae=d+c�Ad=2c+b�Ac=2b+a�Ab=a+1
�@3�@�@�@2�@�@ �@1�@�@�@1
�̂悤�ɂȂ�Ai��89+13�~3��128
�E3�Ԗڂ̐���2�̂Ƃ��A
f�����������𐔂���ƁA
i=h+g�Ah=g+f�Ag=2f+e�Af=2e+d�Ae=d+c�Ad=2c+b�Ac=2b+a�Ab=a+1
�@2�@�@ �@1�@�@�@1
�̂悤�ɂȂ�Ai��89+21�~2��131
�E2�Ԗڂ̐���2�̂Ƃ��A
f�����������𐔂���ƁA
i=h+g�Ah=2g+f�Ag=2f+e�Af=2e+d�Ae=d+c�Ad=2c+b�Ac=2b+a�Ab=a+1
�@1�@�@�@1
�̂悤�ɂȂ�Ai��89+34�~1��123
�E1�Ԗڂ̐���2�̂Ƃ��A
f�����������𐔂���ƁA
i=2h+g�Ah=2g+f�Ag=2f+e�Af=2e+d�Ae=d+c�Ad=2c+b�Ac=2b+a�Ab=a+1
�@1
�̂悤�ɂȂ�Ai��89+55�~1��144
�ȏ�̂悤�ɂǂ��100���Ă��܂��܂��B
��������́A����1�A��2��1�̃t�B�{�i�b�`����ɂȂ��Ă��܂��B
���P�@���݊W���P�A�Q�A�P�A�P�A�R�ƂȂ鐮���̑g���P�ȏ�100�ȉ��͈̔͂ł��ׂċ��߂Ȃ����B
a,b,c,d,e,f�͎��R���Ƃ��E�E�E�@
a��b��1�]��c a>b
a>c
b��c��2�]��d b>c
b>d
c��d��1�]��e c>d c>e
d��e��1�]��f d>e d>f
e��f��3�]��0
e>f a>b>c>d>e>f�E�E�E�A
�@
�A���
a=b+c
b=2c+d
c=d+e
d=e+f
e=3f
���
a=25f
b=18f
����đ�Ӂia��100�j���
1��f��4
(a,b)=(25,18)�A(50,36)�A(75,54)�A(100,72)�E�E�E�E��
���Q�@�P�ȏ�100�ȉ��͈̔͂ő��݊W���ł������Ȃ�悤�Ȑ����̑g�ׂ��Ƃ���A�������X�ł���g���ł������A������1�g��������܂���B����1�g�����߂Ȃ����B
�@�@�@1�ȏ�100�ȉ��̎��R���̑g�́A100*99/2��4950�g����܂��B��������ׂĒ��ׂ�͓̂�V�ł��B
�����Ŗ��1�Ɠ����v�̂ōl���Ă����܂��B
�@�@�@�@�L�����ώG�ɂȂ�̂�abcde�E�E�E���Aa1,a2,a3�E�E�E�Ə��������܂��B�܂�����q1 ,q2 ,q3�E�E�E�Ə��������܂��B
an-1�Ŋ����ďI���ꍇ
a1��a2��q1�]��a3
a2��a3��q2�]��a4
a3��a4��q3�]��a5
�@�@�@�@�E
�@�@�@�@�E
�@�@�@�@�E
an-3��an-2��qn-3�]��an-1
an-2��an-1��qn-2�]��an=0
q>0�@�Aa1> a2> a3> a4>
a5>�E�E�E>an�E�E�E�@
������9�ƌ������́An-2��9�An-1��10�An��11�ł��B
�����A
a9��a10��q9�]��a11=0�E�E�E�A
a1��an-1�Ƃ̊W��������
a1= q1a2+a3
=q1(q2a3+a4)+a3
= q1(q2(q3a4+a5)+a4)+ (q3a4+a5)
= q1(q2(q3(q4
(q5a6+a7)+a6)+ (q5a6+a7))+
(q4(q5a6+a7)+a6))+ (q3(q4(q5a6+a7)+a6)+
(q5a6+a7))
= q1(q2(q3(q4
(q5(q6a7+a8)+a7)+ (q6a7+a8))+
(q5(q6a7+a8)+a7))+ (q4(q5(q6a7+a8)+a7)+
(q6a7+a8)))
+ (q3(q4(q5(q6a7+a8)+a7)+
(q6a7+a8))+ (q5(q6a7+a8)+a7))
= q1(q2(q3(q4
(q5(q6(q7a8+a9)+a8)+
(q7a8+a9))+ (q6(q7a8+a9)+a8))+
(q5(q6(q7a8+a9)+a8)+
(q7a8+a9)))+ (q4(q5(q6(q7a8+a9)+a8)+
(q7a8+a9))+ (q6(q7a8+a9)+a8)))
+ (q3(q4(q5(q6(q7a8+a9)+a8)+
(q7a8+a9))+ (q6(q7a8+a9)+a8))+
(q5(q6(q7a8+a9)+a8)+
(q7a8+a9)))�E�E�E�E�B
�����܂ŏ����܂������A�@�A���
a10>0
a9>1
a8>2
�������܂��̂ŇB��
a9=2�Aa8=3�Aq7=1�i�e�X�̍ŏ��l�j�������Ă݂��
= q1(q2(q3(q4
(q5(q6(4)+3)+ (4))+ (q6(4)+3))+ (q5(q6(4)+3)+
(4)))+ (q4(q5(q6(4)+3)+ (4))+ (q6(4)+3)))
+ (q3(q4(q5(q6(4)+3)+
(4))+ (q6(4)+3))+ (q5(q6(4)+3)+ (4)))
�����q6��2���������
= q1(q2(q3(q4
(q5(15)+ (11))+ (q5(11)+ (4)))+ (q4(q5(11)+
(4))+ (11)))
+ (q3(q4(q5(11)+
(4))+ (11))+ (q5(11)+ (4)))
�����q1�`q5�܂ł��ׂ�1�Ƃ��Ă�108�ƂȂ�out�ł�
�����q1�`q7��1�������܂��i�掮�̌`����q6=1�Aq1�`q5��2�Ƃ����Ƃ���a1������ɑ傫���Ȃ�܂��j
���������ćB�͎��̂悤�ɕό`�ł��܂�
a1= 21a8+13a9
��������ēxa1��a9�Ƃ̊W��������
a1= 21(q8a9+a10)+13a9
�@= 21(q8(q9a10+a11)+a10)+13a9
= 21(q8q9+1)a10+13a9�@�@�@�@�i��A���a11=0�j�E�E�E�C
a10<a9�@����a10��1�Aa9��2�i�e�X�̍ŏ��l�j�Ƃ����Ƃ�q9��2
�C�ɑ�������
a1= 42q8+47�@
q8��1���傫�Ȃ̒l���Ƃ�Ƃ�a1��100���傫���Ȃ�̂�
q8��1
�@�@�@�ȏォ��
�@�@�@�@a 9��2
�@�@�@�@a 10��1
q1�`q8��1�Aq9��2
a1��89�Aa2��55
����ӂɒ�܂�̂�1�g�����Ȃ����Ƃ������܂��E�E�E�E��
���ׂĂ݂�ƃt�B�{�i�b�`����ɂȂ�悤�ł��B�i�����̒藝�i���������̌�����2�{�ȉ��̉ŋ��܂�j������𗘗p���Ă���悤�ł��j
����͎��͂����łǂ��܂ł��邩����Ă݂܂����B�v�Z���ĕ��ׂ�ƃt�B�{�i�b�`����ɂȂ��Ă��܂����B
�u�X���[�N�}���v 10/23
18��34���@��M �X�V 10/28
���365��
�P�ȏ�̂Q�̐������A���i���������͂����傫���j�ɂ��Ď��̂悤�ȑ�����s���B�������Ŋ������Ƃ��̏��������Ă����āA�]�肪������x�������̗]��Ŋ����āA�]��̂������J��Ԃ��B
�Ⴆ�A�����R�P�A�����X�W�̂Ƃ��͂����Ȃ�B
�X�W���R�P���R�A�]��͂T
�R�P���T���U�A�@�]��͂P
�T���P���T�A�]�肪�Ȃ��A����I��
�@���̂Ƃ��A�o�Ă����������ɏ����Ă݂�ƁA�R�A�U�C�T�ł���B
�����ŁA�R�P�ƂX�W�̑��݊W�͂R�C�U�A�T�ł���Ƃ����B�܂��A���݊W�ɏo�Ă��鏤�̌��i�R�P�ƂX�W�̂Ƃ��͂R�j�𑊌݊W�̒����Ƃ����B
�@�Ⴆ�A�W�ƂP�P�̑��݊W�͂P�A�Q�A�P�D�Q�ł���Ƃ����B���̒����͂S�ł���B
���P�@���݊W���P�A�Q�A�P�A�P�A�R�ƂȂ鐮���̑g���P�ȏ�100�ȉ��͈̔͂ł��ׂċ��߂Ȃ����B
��/a=3
��/3a=1...a
��/4a=1...3a
��/7a=2...4a
��/18a=1...7a
�Ō�́�=25a
so...(25,18),(50,36),(75,54),(100,72)
���Q�@�P�ȏ�100�ȉ��͈̔͂ő��݊W���ł������Ȃ�悤�Ȑ����̑g�ׂ��Ƃ���A�������X�ł���g���ł������A������1�g��������܂���B����1�g�����߂Ȃ����B
����ꂸ�ɑ���...�݂��ɑf�ł���...
1,1,2,3,5,8,13,21,34,55,89
89/55=1...34
55/34=1...21
34/21=1...13
21/13=1...8
13/8=1..5
8/5=1...3
5/3=1...2
3/2=1...1
1/1=1 ��9��
so...
(89,55)
