平成３０年１1月25日
[流れ星]
第366回数学的な応募解答
＜解答募集期間：10月28日〜11月25日＞
［ヘロンの四角形］
４辺の長さが４，６，８，１０の四角形の面積が最大となるように、辺の長さの順番を決め、そのときの、面積の最大値を求めてください。
NO1 「スモークマン」 11/01 01時35分 受信
更新 11/25
一般の四角形における面積は調べると...
S=√((s-a)(s-b)(s-c)(s-d)-abcd*(cost)^2)・・・tは対角の和の半分
と表されることを天下りで使えば...
Sはt=90°の時=対角の和180°=円に内接する四角形の時で
問題の□は2^2+3^2+2*2*3*x=4^2+5^2-2*4*5*x
x=7/13<1 と存在できることがわかるので...
Max{S}=√(7-2)(7-3)(7-4)(7-5)=√(5*4*3*2)=2√30
実際は...4倍の8√30
NO2「早起きのおじさん」 11/04 19時37分 受信 更新 11/25
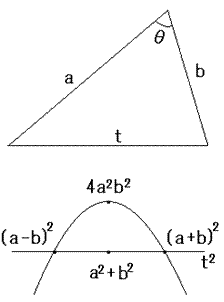●底辺の長さがtで、他の2辺がaとbの三角形の面積Sを
ヘロンの公式で調べます。
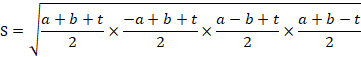
二通りの整理をしましたが、根号の中は、
の2次関数です。
x切片や、最大値は図に書き込んだ通りです。
面積Sの最大値は、
のときで、
一方、別の方法で三角形の面積Sを求めると、
最大値は、θ＝90°のとき、つまり直角三角形のときです。
この2次関数が根号の中に入ったSは定義域が
となります。
●さて、四角形の面積Sを次のように求めます。
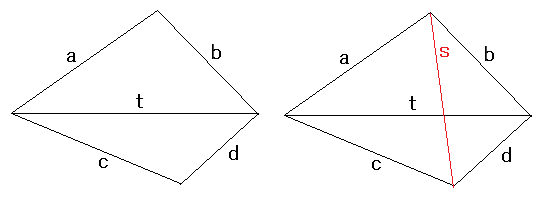
左の図をみてわかりますが、aとb、cとdをそれぞれ入れかえても面積Sは変わりません。
三角形の三辺の長さが変わらないからです。
次に、もう一つの対角線で四角形を二つに分けて、面積を求めることを考えます。
同じ四角形なら、どちらの計算も同じ値になるはずです。
右の図も、aとc、bとdをそれぞれ入れかえて面積Sは変わりません。
ある辺が、他のどの辺と組んでも面積Sが、同じ値になることになります。
つまり、四角形の面積は、辺の順番によりません。
●aを最大の長さの辺とし、aとcをそれぞれのペアの長い方の辺と考えます。
4辺を、｛10，8，6，4｝とすると、
どの場合も、差か和が等しくなります。
ここで、
とおくと、
このグラフの概形は、次のようになります。
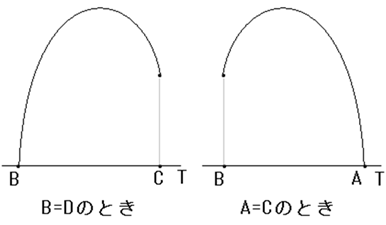
●B＝Dとして、四角形の面積Sを調べてみます。
A＝Cのときも、同じような経過になります。
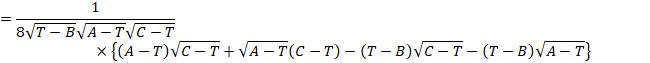
導関数が0の場合は、分子が0のときなので、
左辺は、
右辺は、
整理すると、Tの1次式になります。
これを、Sの式に入れると、
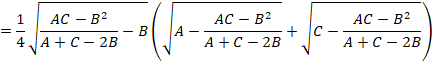
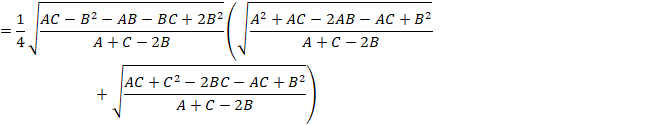
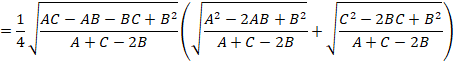
B=Dなので、この式を次のように変形します。
だったので、もとに戻すと、
10、8、6、4の値を代入すると、
「早起きのおじさん」 11/16 16時06分 受信 更新 11/25
366解答続き 早起きのおじさん
●前の解答は、
『aを最大の長さの辺とし、aとcをそれぞれのペアの長い方の辺と考えます。
4辺を、｛10，8，6，4｝とすると、
どの場合も、差か和が等しくなります。
そこで、
a−b＝c−d
として、四角形の面積Sを調べてみます。
』
という流れでした。
ここで、aとdをそれぞれのペアの長い方の辺と考えます。
すると、差が等しい場合は、a−b＝d−c
変形すると、a＋c＝b＋d
これは、向かい合う二辺の和が等しいことを示します。(左図)
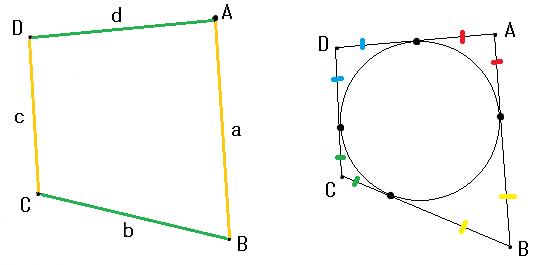
●円に外接する四辺形は、向かい合う二辺の和が等しくなります。
これは、右図からわかります。
●次に、向かい合う二辺の和が等しい四辺形が、円に外接することを調べます。
aが一番長い辺とすると、cが一番短くなります。
CD＝DE、EA＝AFとなるように、点E、Fをとります。
すると、向かい合う二辺の和が等しいので、FB＝BCとなります。
3つの三角形、△DCE、△AEF、△BFCはいずれも二等辺三角形です。
この3つの二等辺三角形の各頂点から対辺に垂線を下します。
すると、1点Oで交わります。
この点Oは、3つの二等辺三角形の底辺からなる△CEFの外心となります。
3つの垂線が△CEFの各辺の垂直二等分線になるからです。
点Oから、四辺形の各辺に垂線を下します。
例えば、2つの直角三角形、△ODIと△ODJは、斜辺と1鋭角が等しいので合同になります。
よって、OI＝OJです。
同様にして、OJ＝OG、OG=OHとなるので、OI＝OJ＝OG＝OHです。
Oを中心とし、半径OIの円が四角形ABCDに内接します。
よって、向かい合う二辺の和が等しい四辺形は、円に外接することがわかります。
●次に、円に内接する四辺形ABCDの面積Sを調べてみます。
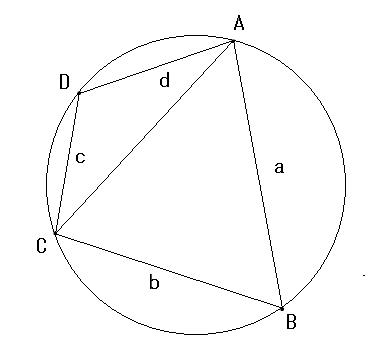
よって、
一方、△ABCから、
△CDAから、
よって、
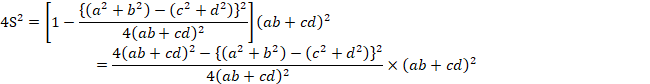
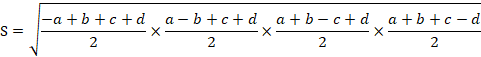
ここで、この四辺形が円に外接しているとします。
つまり、a＋c=b＋d です。
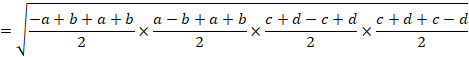
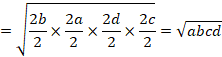
前の解答から、2組の2辺の差が等しい四辺形の面積の最大値は、
でした。
●まとめると、
「4辺が与えられた四辺形が円に外接するとき、最大が面積値をとるのは、別の円に内接しているとき」
ということになります。
皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。
