�����R�P�N�P���Q�O��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��368�����w�I�ȉ����
�@�@�@�@����W���ԁF12��23���`1��20����
�m2019��31�̖��n
2018�N���c��1�T�ԁB���܂ł̂�����ɐ[�����Ӑ\���グ�܂��B
����2019�N���������������ڎ���܂��悤��낵�����肢�������܂��B
�����ŁA���N�̐���2019�N�ƕ����Ō��31�N�ɂ��Ȃ�ŁA��₵�܂����B
���P�F31�ɂT�����������͂X�Ŋ����A�t�ɂX�����������͂T�Ŋ����܂��B����ł́A31�ɂ������������͂��Ŋ����A�t�ɂ����������炁�Ŋ����鎩�R���i���A���j�̑g��T���Ă��������B�������A�������Ƃ���B
�@���݁A���ɂS�g�������Ă��܂����A���̑g�����邩������܂���B�����Ă��������B
���Q�F2019�ɂ������������͂��Ŋ����A�t�ɂ����������炁�Ŋ����鎩�R���i���A���j�̑g��T���Ă��������B�������A�������Ƃ���B
�@���݁A�U�g�������Ă��܂����A���̑g�����邩������܂���B�����Ă��������B
���R�F���鐔��31������������2019�Ŋ����A�t��2019������������31�Ŋ����鐔�������Ă��������B
�@
NO1�u�X���[�N�}���v 12/24 12��58���@��M
�X�V 1/20
���N���X�g�����Ƀ`�������W!! (���1,2�́A���3����̕����ōl�������Ă݂����̂��㔼�ɒlj������Ă��炢�܂��� ^^)
���P�F31�ɂT�����������͂X�Ŋ����A�t�ɂX�����������͂T�Ŋ����܂��B����ł́A31�ɂ������������͂��Ŋ����A�t�ɂ����������炁�Ŋ����鎩�R���i���A���j�̑g��T���Ă��������B�������A�������Ƃ���B
�@���݁A���ɂS�g�������Ă��܂����A���̑g�����邩������܂���B�����Ă��������B
31+1=32
32=2^5�E�E�E2,2^2,2^3,2^4,2^5
31+2=33
33=3*11�E�E�E3,11
31+3=34
34=2*17�E�E�E17
31+4=35
35=5*7�E�E�E5
31+5=36
36=2^2*3^2�E�E�E4,9
���Q�F2019�ɂ������������͂��Ŋ����A�t�ɂ����������炁�Ŋ����鎩�R���i���A���j�̑g��T���Ă��������B�������A�������Ƃ���B
�@���݁A�U�g�������Ă��܂����A���̑g�����邩������܂���B�����Ă��������B
2019+1=2020
2020=2^2*5*101�E�E�E2,4,5,10,20,101,202,404,505,1010,2020
2019+2=2021
2021=43*47�E�E�E43,47,2021
2019+3=2022
2022=2*3*337�E�E�E6,3*337=1011
2019+4=2023
2023=7*17^2�E�E�E17,17^2=308
�Ȃǁc
���R�F���鐔��31������������2019�Ŋ����A�t��2019������������31�Ŋ����鐔�������Ă��������B
x+2019=31m
x+31=2019n
2019-31=31m-2019n
1988+2019n=31m
m=64+65n+4(1+n)/31
so�cn=31k-1
m=64+65(31k-1)+4k=2019k-1
so�c
x=31(2019k-1)-2019=62589k-2050
so�c
60539
123128
185717
�c
���̕��@�����c
(���1)���c
31=b(ak-1)-a
=abk-(a+b)
31+(a+b)=abk�E�E�E1<=k
31+(1+2)=2k�ck<=17 �ƍl�������c
k=1
(a,b)=(2,33),(3,17),(5,9)
k=2
(a,b)=(1,32),(2,11),(4,5)
k=3
(a,b)=(1,16)
k=4�c�Ȃ�
k=5
(a,b)=(1,8)
k=6
(a,b)=(2,3)
k=7�c�Ȃ�
k=8...�Ȃ�
k=9
(a,b)=(1,4)
k=10�c�Ȃ�
k=11�c�Ȃ�
k=12�c�Ȃ�
k=13�c�Ȃ�
k=14�c�Ȃ�
k=15�c�Ȃ�
k-16�c�Ȃ�
k=17
(a,b)=(1,2)
k=17�̂Ƃ��Aa<2 �Ȃ̂ŁA
a-1�̎��`�F�b�N
a=1�c���ׂďo�Ă�
so�c11���ȁH
(���2)���c
2019=b(ak-1)-a
2019+a+b=abk
2019+1+2=2k�E�E�E1<=k<=1011
2019+1+x=x^2
x=45.45�c
�Ȃ̂ŁA
k=46�܂Œ��ׂĂ݂܂����c
k=1
(a,b)=(2,2021),(3,1011),(5,506),(6,405),(11,203)
k=2
(a,b)=(1,2020),(4,289)
k=3
(a,b)=(1,1010),(9,78)
k=4�c�Ȃ�
k=5
(a,b)=(1,505)
k=6
(a,b)=(1,404)
k=7�c�Ȃ�
k=8�c�Ȃ�
k=9
(a,b)=(5,46)
k=10�ȍ~�c
(a,b)=(1,202),(1,101),(2,47),(2,43),(4,17),(5,11),
k=47�̎��ca<6.57�c
�Ȃ̂��c
6�ȉ���a�ŒT���c
a=6�c���łɂłĂ���̂���
a=5�c(5,11)���lj�
a=4�c(4,17)���lj�
a=3�c���łɂłĂ���̂���
a=2�c(2,43(,(2,47)���lj�
a=1�c(1,10),(1,20)���lj�
���c24���Ȃ��c?
NO2�u�O�p��K�v
01/01 19��59���@��M �X�V 1/20
�� ��368��@�����O�p��K��
�y���P�z
�@��ӂ��m�Cn (m��n)�����R���Ƃ���
31�{a��mb �c�@�C 31�{b��na �c�A
�����藧�B�@�A���b�����������
(mn�|1)a��31(m�{1) �c�B
[�T] a��31�̔{���ł͂Ȃ��ꍇ
�@�B��� mn�|1 ��31�̔{���ƂȂ邩��Ck�����R���Ƃ��� mn�|1��31k �B
(�@) k��1 �̂Ƃ��@mn��32��25 �c�C
�� (m, n)��(1, 32), (2, 16), (4, 8)
�@�����̂Ƃ��C�B�A��菇�ɁC (a, b)��(2, 33), (3, 17), (5, 9)
(�A) k��2, 3, �c �Ƃ��ē��l�Ɍv�Z�����
(a, b)��(1, 32), (2, 11), (4, 5), (1, 16), (1, 8), (2, 3), (1, 4) ����B
[�U] a��31�̔{�� a��31k (k��1, 2, �c) �̂Ƃ�
�@�B���Ck(mn�|1)��m�{1 �c�D
k��1,
2, �c �Ƃ��ćD���m, n���߇B�A���a, b�����߂��
(a, b)��(31, 62), (62, 93) ��B
�y���Q�z
�@��ӂ��m�Cn (m��n)�����R���Ƃ���
2019�{a��mb �c�@�C 2019�{b��na �c�A
�����藧�B�@�A���b�����������
(mn�|1)a��2019(m�{1)��3�673(m�{1) �c�B
[�T] mn�|1��3k (k��1, 2, �c) �̏ꍇ
(�@) k��1 �̂Ƃ��Cmn��4�C(m, n)��(1, 4) �c�C
���̂Ƃ��C�A�B�C��� (a, b)��(1346, 3365)
(�A) k��2, 3, �c �Ƃ��ē��l�Ɍv�Z����� (a, b)��(673, 1346), (673, 1346) ��B
[�U] mn�|1��673k (k��1, 2, �c) �̏ꍇ
(�@) k��1 �̂Ƃ��Cmn��674�C(m, n)��(1, 674), (2, 337) �c�D
���̂Ƃ��C�A�B�D��菇�� (a, b)��(6, 2025), (9, 1014)
(�A) k��2, 3, �c �Ƃ��ē��l�Ɍv�Z�����
�@ (a, b)��(3, 2022), (6, 675), (2, 2021), (3, 1011), (5, 506), (6, 405), (11, 203),
(21, 102), (6, 225), (4, 289), (27, 33) ����B
[�V] mn�|1��k(m�{1) (k��1, 2, �c) �̏ꍇ
(�@) k��1 �̂Ƃ��Cmn�|1��m�{1�Cm(n�|1)��2�C(m, n)��(1, 3) �c�E
���̂Ƃ��C�A�B�E��� (a, b)��(2019, 4038)
(�A) k��2, 3, �c �Ƃ��ē��l�Ɍv�Z����� (a, b)��(673, 2692) ��B
�y���R�z
�@��ӂ��x, m�Cn (m��n)�����R���Ƃ���
x�{31��2019m
�c�@�C x�{2019��31n �c�A
�@�@�A���C
�@�@�@3�673m�|31��31n�|3�673�@ �� 3�673(m�{1)��31(n�{1) �c�B
�@3, 31, 673�݂͌��ɑf������k��1, 2, �c�Ƃ���
�@�@�@m�{1��31k
, n��3�673k �c�C
�@�@�A�C���, x��3�673(31k�|1)�|31��3�31�673k�|2050
��60593, 123128, 185717, �c
NO3�u���N���̂�������v 01/03 17��27���@��M �X�V 1/20
���1
31��5(a)�����������́A9(b)�Ŋ����܂��B
����͎��̂悤�ɍl����Ɣ[���ł��܂��B
31��9�Ŋ������Ƃ��̏��Ɨ]��ŕ\���܂��B
�����5��������ƁA�]��Ƃ̘a��9�ɂȂ邩��ł��B
31�{5��(9�~3�{4)�{5��9�~3�{(4�{5)��9�~3�{9��9�~(3�{1)
31��b�Ŋ������Ƃ��̗]��Ƃ̘a��b�ɂȂ�悤�Ȑ���a�̌��ɂȂ�܂��B
31�Ƃ��̂悤��a�Ƃ̘a�͕K��b�Ŋ����܂����A31��b�Ƃ̘a��a�Ŋ�����Ƃ͌���܂���B
�ꍇ�̐������������Ȃ��̂ŁA����݂Ԃ��ɒ��ׂĂ݂܂��B
���悸�A![]() �Ƃ��āA���ׂĂ݂܂��B
�Ƃ��āA���ׂĂ݂܂��B
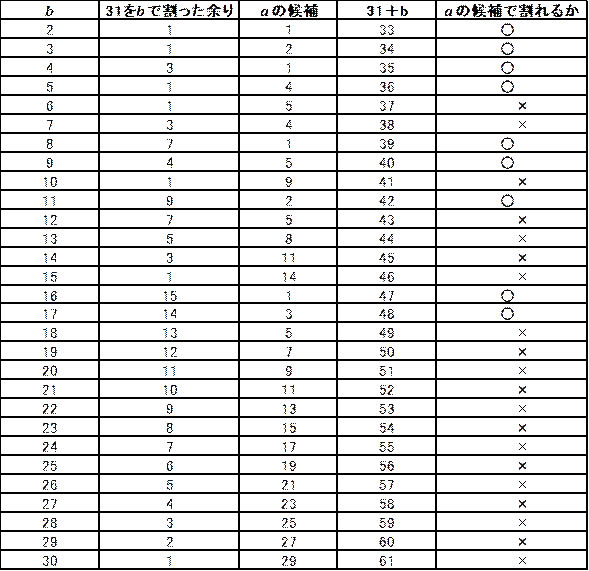
���̌��ʁA���� (a,b) ��������܂��B
(1,2)�A(2,3)�A(1,4)�A(4,5)�A(1,8)�A(5,9)�A(2,11)�A(1,16)�A(3,17)
������b��31�ɂȂ邩���l���܂����A����͂���܂���B
31��31��菬���Ȑ��Ƃ̘a���A31�Ŋ����邱�Ƃ��Ȃ�����ł��B
���Ō�ɁAb��31���傫�ȏꍇ���l���܂��B
31��a���̘a��b�Ŋ�����̂ŁA
b��31�{a
�܂��A31��b�Ƃ̘a���Aa�Ŋ�����̂ŁA��̗��ӂ�31�������āA
![]()
a��62�̖łȂ���ΐ����ɂȂ�Ȃ��̂ŁA
a��1�C2�C31�C62
����āA
(1,32)�A(2,33)�A(31,62)�A(62,93)
���2
���1�ɔ�ׂďꍇ�̐��������̂ŕʂ̂��������܂��B
�悸b���A2019��菬�����ꍇ���݂܂��B
��a��1�̂Ƃ��Ab�̒l�ɊW�Ȃ��A2019�{b ��a�Ŋ����̂ŁA
2019��b�~q�{(b�|1) �Ƃ���ƁA2020��b�~(q�{1)�D
2020��2�~2�~5�~101�Ȃ̂ŁA
2019��2�~1009�{1
2019��4�~504�{3
2019��5�~403�{4
2019��10�~201�{9
2019��20�~100�{19
2019��101�~19�{100
2019��202�~9�{201
2019��404�~4�{403
2019��505�~3�{504
2019��1010�~1�{1009
����āA
(1,2)�A(1,4)�A(1,5)�A(1,10)�A(1,20)�A(1,101)�A(1,202)�A(1,404)�A(1,505)�A(1,1010)
��a��2�̂Ƃ��Ab����Ȃ�A2019�{b ��a�Ŋ����̂ŁA
2019��b�~q�{(b�|2) �Ƃ���ƁA2021��b�~(q�{1)�D
2021��43�~47�Ȃ̂ŁA
2019��43�~46�{41
2019��47�~42�{45
����āA
(2,43)�A(2,47)
��a��3�̂Ƃ��Ab���e�ʂ̐��̘a��3�̔{���Ȃ�A2019�{b ��a�Ŋ����̂ŁA
(2019��3�̔{��)
2019��b�~q�{(b�|3) �Ƃ���ƁA2022��b�~(q�{1)�D
2022��2�~3�~337�Ȃ̂ŁA
(b�́Aa���傫��)
2019��6�~336�{3�@�@�@
��
2019��337�~5�{334�@�@ �@�~
2019��674�~2�{671�@�@ �@�~
2019��1011�~1�{1008�@ ��
����āA
(3,6)�A(3,1011)
��a��4�̂Ƃ��A2019�{b �̉�2����4�̔{���Ȃ�a�Ŋ����̂ŁA
2019��b�~q�{(b�|4) �Ƃ���ƁA2023��b�~(q�{1)�D
2023��7�~17�~17�Ȃ̂ŁA
(b�́Aa���傫��)
2019��7�~288�{3�@�@�@ 2019�{b��2026�@�@�@�~
2019��17�~118�{13�@�@
2019�{b��2036�@�@��
2019��119�~16�{115�@�@2019�{b��2138�@�@�@�~
2019��289�~6�{285�@�@ 2019�{b��2308�@�@��
����āA
(4,17)�A(4,289)
��a��5�̂Ƃ��A2019�{b �̉�1����0��5�Ȃ�a�Ŋ����̂ŁA
2019��b�~q�{(b�|5) �Ƃ���ƁA2024��b�~(q�{1)�D
2024��2�~2�~2�~11�~23�Ȃ̂ŁA
(b�́Aa���傫��)
2019��8�~252�{3�@�@�@
2019�{b��2027�@�@�@�~
2019��11�~183�{6�@�@
2019�{b��2030�@�@��
2019��22�~91�{17�@�@ 2019�{b��2041�@�@�@�~
2019��44�~45�{39�@�@
2019�{b��2063�@�@�@�~
2019��88�~22�{83�@�@�@
2019�{b��2107�@�@�@�~
2019��23�~87�{18�@�@
2019�{b��2042�@�@�@�~
2019��46�~43�{41�@�@ 2019�{b��2065�@�@��
2019��92�~21�{87�@�@
2019�{b��2111�@�@�@�~
2019��184�~10�{179�@�@�@2019�{b��2203�@�@�@�~
2019��253�~7�{248�@�@ 2019�{b��2272�@�@�@�~
2019��506�~3�{501�@ �@2019�{b��2525�@�@��
2019��1012�~1�{1007�@�@ 2019�{b��3031�@�@�@�~
����āA
(5,11)�A(5,46)�A(5,506)
��a��6�̂Ƃ��Ab������e�ʂ̐��̘a��3�̔{���Ȃ�A2019�{b ��a�Ŋ����̂ŁA
2019��b�~q�{(b�|6) �Ƃ���ƁA2025��b�~(q�{1)�D
2025��3�~3�~3�~3�~5�~5�Ȃ̂ŁA
(b�́Aa���傫��)
2019��9�~224�{3�@�@�@
��
2019��27�~74�{21�@�@ ��
2019��81�~24�{75�@�@ ��
2019��15�~134�{9�@�@ ��
2019��45�~44�{39�@ �@��
2019��135�~14�{129�@�@ ��
2019��405�~4�{399�@�@ ��
2019��25�~80�{19�@�@ �@�~
2019��75�~26�{69�@�@ ��
2019��225�~8�{219�@�@�@ ��
2019��675�~2�{669�@�@ ��
����āA
(6,9)�A(6,27)�A(6,81)�A(6,15)�A(6,45)�A(6,135)�A(6,405)�A(6,75)�A(6,225)�A(6,675)
�����ς��܂��B
�����̉����݂Ă����܂��B
��2019��3�~673��3�~(2�~336�{1)��6�~336�{3�Ȃ̂ŁA(3,6) �����ł��邱�Ƃ͂����ɕ�����܂��B
(����́A���o�ł�)
�܂��A
2019��673�~3��673�~(2�{1)��673�~2�{673�Ȃ̂ŁA(673,1346) �����ł��邱�Ƃ������ɕ�����܂��B
�����̍l���Œ��ׂ܂��B
31��5(a)�����������́A9(b)�Ŋ����܂��B
����͎��̂悤�ɍl����Ɣ[���ł��܂��B
31��9�Ŋ������Ƃ��̏���傫�����ďC����������5��������ƁA9�̔{���ɂȂ邩��ł��B
31�{5��(9�~4�|5)�{5��9�~4
x��y�Ƃ��āA���̎�����������Ƃ��܂��B
2019��3�~673��3�~(y�~p�|x)��3y�~p�|3x
2019��3�~673��3�~(x�~q�|y)��3x�~q�|3y
����ƁA(3x,3y)�����ł��邱�Ƃ��킩��܂��B
3x���A3��6�̂Ƃ��͏�Œ��ׂĂ���̂ŁA9�����ׂ܂��B
���ۂɂ́A3�ŖāA
673��yp�|x
673�{x��yp�Ƃ��āA�f�����������Ė�(y�̌��)��T���A673�{y��x�Ŗ邩�ׂ܂��B
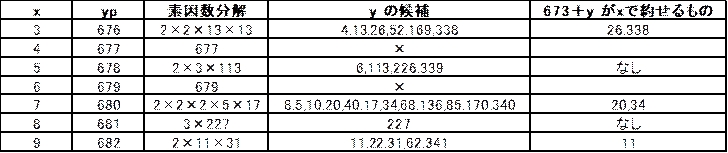
�\���A3�{���āA
(9,78)�A(9,1014)�A(21,60)�A(21,102)�A(27,33)
�����̎����l���܂��B
![]()
���ꂪ���藧���Ă���ƁA2019��a�𑫂���b�Ŋ����Ab�𑫂���a�Ŋ����܂��B
�ό`���āA
![]()
2019��a�������āA�������������Ƃ��Aa�|1�������Ɏ������ׂ�悢���ƂɂȂ�܂��B
���܂Œ��ׂĂ��Ȃ��Aa�Ƃ��āA
7�A8�A10�A11�A13�A14�A16�A17�A19�A20�A22�A23�A25�A26�A28�A29�A30�A����
�ׂ܂��B
![]()
![]() �f��
�f��
![]() �f��
�f��
![]()
![]()
![]()
![]()
![]()
![]()
![]() �f��
�f��
![]()
![]()
![]()
![]()
![]()
![]()
![]()
�����܂ł́A(11,203) ������܂��B
���̕��@�łǂ��܂ł��悢�̂����l���܂��B
![]() �����藧��ԑ傫��a��b���Ȃ�ׂ��������Ƃ��ł��B
�����藧��ԑ傫��a��b���Ȃ�ׂ��������Ƃ��ł��B
a��b �Ȃ̂ŁA
![]()
�Ƃ��āA
![]()
![]()
![]()
�ƂȂ�̂ŁA45�܂Œ��ׂ܂��B
![]()
![]()
![]()
![]() �f��
�f��
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() �f��
�f��
![]()
�ƂȂ�̂ŁAa�́A31����2017�܂ł͈̔͂ɂ́A��������܂���B
���Ō�ɁAb��2019���傫�ȏꍇ���l���܂��B
2019��a���̘a��b�Ŋ�����̂ŁA
b��2019�{a
�܂��A2019��b�Ƃ̘a���Aa�Ŋ�����̂ŁA��̗��ӂ�2019�������āA
![]()
a��4038�̖łȂ���ΐ����ɂȂ�Ȃ��̂ŁA
a��1�C2�C3�C6�C673�C1346�C2019�C4038
����āA
(1,2020)�A(2,2021)�A(3,2022)�A(6,2025)�A(673,2692)�A(1346,3365)�A(2019,4038)�A(4038,6057)
���3
���鐔��N�Ƃ��܂��B
���鐔�ɁA31������������2019�Ŋ����̂ŁAN��2019�~p�|31�D
���鐔�ɁA2019������������31�Ŋ����̂ŁAN��31�~q�|2019�D
����āA
2019�~p�|31��31�~q�|2019
2019�~(p�{1)��673�~3�~(p�{1)��31�~(q�{1)
2019��31�́A�݂��ɑf�Ȃ̂ŁA
p�{1��31k
q�{1��2019k
p��31k�|1�Ƃ���Ƃ��鐔N�́A
N��2019�~(31k�|1)�\31��62589k�|2050�D
