平成３１年２月１７日

[流れ星]

　　　　第369回数学的な応募解答

　　　　＜解答募集期間：1月20日〜2月17日＞

［割り算の剰余］

　お詫び　前回の問題で答えがすべて解っていないまま出題したことを深くお詫び申し上げます。

　過去の神戸大学の入試問題から出題します。

問題１　ｘの整式Ｐ(ｘ)をｘ−１で割った余りが１、x−2で割った余りが２、ｘ−３で割った余りが３となった。

Ｐ(ｘ)を(ｘ−１)(ｘ−２)(ｘ−３)で割った余りを求めよ。

問題２　ｎを2以上の自然数とする。ｋ＝１,２,３,・・・,ｎについて、
整式Ｐ(ｘ)をｘ−ｋで割った余りがｋとなった。

Ｐ(ｘ)を(ｘ−１)(ｘ−２)・・・(ｘ−ｋ)で割った余りを求めよ。

ヒント　Ｐ(ｘ)の表し方に工夫してください。

NO1「早起きのおじさん」 01/23 20時42分　受信 更新 2/17

●P(x) を x−1 で割った商を q₁(x) 、x−2 で割った商を q₂(x)とすると、

P(x) を (x−1)(x−2) で割った商を q₁₂(x) とすると、余りは除式より次数が低いので、

P(1)＝1、P(2)＝2 なので、

よってP(x) を (x−1)(x−2) で割った余りは、x です。

問題1

●P(x) を x−1、x−2、x−3 で割った商をそれぞれq₁(x)、q₂(x)、q₃(x)とすると、

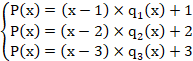
P(x) を (x−1)(x−2)(x−3) で割った商を q₁₂₃(x) とすると、余りは除式より次数が低いので、

P(1)＝1、P(2)＝2、P(3)＝3 なので、

よってP(x) を (x−1)(x−2)(x−3) で割った余りは、x です。

●この方法でこの先を計算するのは大変ですが、以下の結果を想像させます。

P(x) を (x−1)(x−2)･･･(x−k) で割った商を q_12･･･k(x) とすると、余りはx となる。

試してみると、

P(x) は (x−j) で割ると、余りはj です。

問題2

●P(x) を x−k で割った商を q_k(x) とすると、

つまり、

同様に、

・・・

ここで黄色の部分は、等しくなります。

とおきます。

Q(1)＝Q(2)＝･･･＝Q(k)＝0 なので、Q(x) は、(x−1)(x−2)･･･(x−k) を因数に持ちます。

Q(x)を(x−1)(x−2)･･･(x−k) で割った商を q_12･･･k(x) とすると、

となります。

NO2「浜田明巳」 　　01/24 11時27分　受信 更新 2/17

まず問題２を解いてから，問題１を解く．
問題２
　ｋ＝１，２，３，・・・，ｎ（ｎ≧２）のとき，ｘの整式Ｐ(ｘ)をｘ−ｋで割った余りはｋである．
　Ｐ(ｘ)を(ｘ−１)(ｘ−２)(ｘ−３)・・・(ｘ−ｋ)で割った余りは？

i). ｋ＝１のとき，Ｐ(ｘ)をｘ−１で割った余りは，１である．
i). ｋ≧２のとき，
　Ｐ(ｘ)をｋ次式(ｘ−１)(ｘ−２)(ｘ−３)・・・(ｘ−ｋ)で割った商をＱ(ｘ)，余りは，高々(ｋ−１)次式であるので，
　　ａ_０＋ａ_１ｘ＋ａ_２ｘ^２＋・・・＋ａ_ｋ−１ｘ^ｋ−１・・・（＊）
とすると，
　　Ｐ(ｘ)＝(ｘ−１)(ｘ−２)(ｘ−３)・・・(ｘ−ｋ)Ｑ(ｘ)＋ａ_０＋ａ_１ｘ＋ａ_２ｘ^２＋・・・＋ａ_ｋ−１ｘ^ｋ−１
　条件より，
　　Ｐ(１)＝ａ_０＋ａ_１＋ａ_２＋・・・＋ａ_ｋ−１＝１
　　Ｐ(２)＝ａ_０＋２ａ_１＋２^２ａ_２＋・・・＋２^ｋ−１ａ_ｋ−１＝２
　　Ｐ(３)＝ａ_０＋３ａ_１＋３^２ａ_２＋・・・＋３^ｋ−１ａ_ｋ−１＝３
　　・・・
　　Ｐ(ｋ)＝ａ_０＋ｋａ_１＋ｋ^２ａ_２＋・・・＋ｋ^ｋ−１ａ_ｋ−１＝ｋ
　係数に注意すると，このａ_０〜ａ_ｋ−１の連立方程式の解の１つは，明らかに，
　　ａ_１＝１，ａ_０＝ａ_２＝ａ_３＝ａ_４＝・・・＝ａ_ｋ−１＝０・・・（＊＊）
　また，条件より，余り（＊）は一意的に存在する．
　故に，（＊＊）だけがこの連立方程式の解である．
　故に，余りはｘである．
　まとめると，
　　ｋ＝１のとき，１，ｋ≧２のとき，ｘである．

問題１
　問題２の解答より，余りはｘである．

NO3「にいばりZ12」　　　01/25 23時36分　受信 更新 2/17

問題１　ｘの整式Ｐ(ｘ)をｘ−１で割った余りが１、x−2で割った余りが２、ｘ−３で割った余りが３となった。

Ｐ(ｘ)を(ｘ−１)(ｘ−２)(ｘ−３)で割った余りを求めよ。

解答　P(x)を割り切れる項と割り切れない項である次の2項に分けます。

Ｐ(ｘ)＝(x-1)(x-2)(x-3)Ｃ+x 　　　（Ｃは任意多項式）

(x-1)で割ると商は

(x-2)(x-3)Ｃ+1

余りは

1

(x-2)で割ると商は

(x-1)(x-3)Ｃ+1

余りは

2

(x-3)で割ると商は

(x-1)(x-2)Ｃ+1

余りは

3

P(x)を(x-1)(x-2)(x-3)で割ると商はC

余りは

xとなります・・・回答

問題２　ｎを2以上の自然数とする。ｋ＝１,２,３,・・・,ｎについて、
整式Ｐ(ｘ)をｘ−ｋで割った余りがｋとなった。

Ｐ(ｘ)を(ｘ−１)(ｘ−２)・・・(ｘ−ｋ)で割った余りを求めよ。

解答　問題1と同様にP(x)を割り切れる項と割り切れない項である次の2項に分けます。

Ｐ(ｘ)＝(x-1)(x-2)(x-3)・・・・(x-k)Ｃ+x 　　　（Ｃは任意多項式）

(x-k)で割ると商は

(x-1)(x-2)・・・(x-k+1)Ｃ+1

余りは

k

P(x)を(x-1)(x-2)(x-3) ・・・・(x-k)で割ると商はC

余りは

xとなります・・・回答

「にいばりZ12」　　　01/30 22時27分　受信 更新 2/17

問題２　a_kを2以上の自然数とする。a_ｋ＝ａ₁, ａ₂, ａ₃,・・・, ａ_nについて、
整式Ｐ(ｘ)をｘ−a_ｋで割った余りがa_ｋとなった。（つまり(ｘ−ａ₁)で割ったらあまりａ_1、(ｘ−ａ₂)で割ったらあまりａ_{2・・・、}(ｘ−ａ_n)で割ったらあまりａ_n）

Ｐ(ｘ)を(ｘ−ａ₁)(ｘ−ａ₂)・・・(ｘ−ａ_n)で割った余りを求めよ。

整式Ｐ(ｘ)をｘ−ｋで割った余りがｋとなるためには

解答　問題1と同様にP(x)を割り切れる項と割り切れない項である次の2項に分けます。

Ｐ(ｘ)＝(x-ａ₁)(x-ａ₂)(x-ａ₃)・・・・(x-ａ_n)Ｃ+x 　　　（Ｃは任意多項式：Ｃの最高次数をTとしＰ(ｘ) の最高次数k+Tとする）

整式Ｐ(ｘ)をｘ−ｋで割った余りがｋとなるためには割り切れない項がｘである必要があります

∵余りがｘ-（ｘ-ａ_k）＝ａ_k

(x-ａ₁)(x-ａ₂)(x-ａ₃)・・・・(x-ａ_n)で割ると商は

Ｃ

余りは

xとなります・・・回答

問題２-1

　　問題2の整式Ｐ(ｘ)の最高次数をｋとしたときのＰ(ｘ)を求めよ

解答Ｐ(ｘ)＝(x-ａ₁)(x-ａ₂)(x-ａ₃)・・・・(x-ａ_n)Ｃ+x 　　　（Ｃは0より大きい任意自然数とする）

NO4「kasama」　　　02/09 20時55分　受信 更新 2/17

問題１

P(x)を(x-1)(x-2)(x-3)で割ったとき、商をQ(x)、余りをR(x)とすると、

　P(x)=(x-1)(x-2)(x-3)Q(x)+R(x)

と表せますが、R(x)の次数は高々2なので、

　R(x)=a₂x²+a₁x+a₀

と書くことができます。これに、文章中の条件を当てはまると、

x-1で割った余りが1	⇒	P(1)=1	⇒	a2+a1+a0=1
x-2で割った余りが2	⇒	P(2)=2	⇒	2^2a2+2a1+a0=2
x-3で割った余りが3	⇒	P(3)=3	⇒	3^2a2+3a1+a0=3

これらを解くと、a₂=0、a₁=1、a₀=0なので、余りR(x)は

　R(x)=x

です。

問題２

前問を一般化すると、

　P(x)=(x-1)…(x-k)…(x-n)Q(x)+R(x)

　R(x)=a₀x⁰+a₁x¹+…+a_n-2x^n-2+a_n-1x^n-1

です。これに条件を当てはめて、

x-1で割った余りが1

⇒

P(1)=1

⇒

a0･1^0

+

a1･1^1

+

…

+

an-2･1^n-2

+

an-1･1^n-1

=

1

x-2で割った余りが2

⇒

P(2)=2

⇒

a0･2^0

+

a1･2^1

+

…

+

an-2･2^n-2

+

an-1･2^n-1

=

2

x-3で割った余りが3

⇒

P(3)=3

⇒

a0･3^0

+

a1･3^1

+

…

+

an-2･3^n-2

+

an-1･3^n-1

=

3

…

x-kで割った余りがk

⇒

P(k)=k

⇒

a0･k^0

+

a1･k^1

+

…

+

an-2･k^n-2

+

an-1･k^n-1

=

k

…

x-(n-1)で割った余りがn-1

⇒

P(n-1)=n-1

⇒

a0･(n-1)^0

+

a1･(n-1)^1

+

…

+

an-2･(n-1)^n-2

+

an-1･(n-1)^n-1

=

n-1

x-nで割った余りがn

⇒

P(n)=n

⇒

a0･n^0

+

a1･n^1

+

…

+

an-2･n^n-2

+

an-1･n^n-1

=

n

行列で表現すると、

　　　＝　

です。この行列Aのi行j列目の要素はxij=ij-1なので、Vandermondeの行列式によると

det|A|＝≠0

よって、この連立方程式には解が存在します。Cramerの公式を使って、a0⃣　a1　a2　…　　an-2　an-1　を随時求めると、

・・・・・・・・・・・・

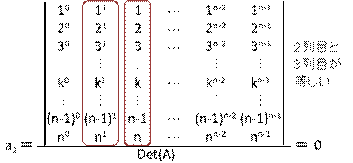
つまり、a₁=1、他は0です。よって、求める余りは、

　R(x)=x　　です。

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。