平成３１年３月１７日
[流れ星]
第370回数学的な応募解答
＜解答募集期間：２月17日〜３月17日＞
［三角形の五心］
高校の総合学習で扱った問題です。
NO1「早起きのおじさん」 02/21 20時44分 受信 更新 3/17
問題1
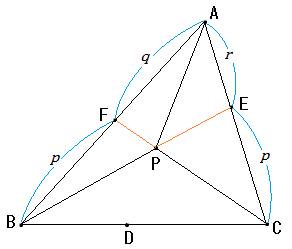
図のように、
APの延長とBCの交点をD、
BPの延長とCAの交点をE、
CPの延長とABの交点をFとします。
△PBC：△PAB＝p：rなのでCE：EA＝p：r、
△PCA：△PBC＝q：pなのでAF：FB＝q：pです。
とします。
を確認しておきます。
先ず、
次に、
(1) 
と(2)をくらべて、
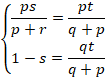
上の式から、
下の式に入れて、
これを(2)に入れると、
問題2
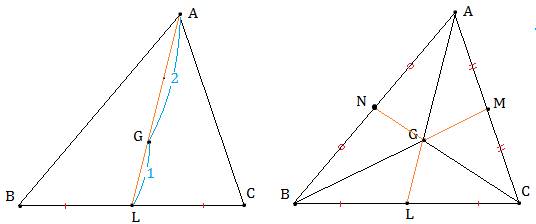
辺BCの中点をL、辺CAの中点をM、辺ABの中点をNとします。
その1
重心は、中線を頂点の方から2：1に内分する点なので、
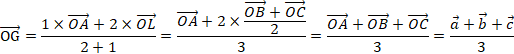
その2
重心は、3中線の交点なので、
△GBC：△GCA：△GAB＝1：1：1です。
問題1のp＝q＝r＝1とすると、
問題3
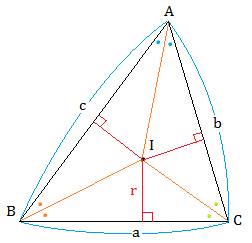
内心から各辺までの距離rが等しいので、
なので、
△IBC：△ICA：△IAB＝a：b：cです。
問題1のp＝a、q＝b、r＝cとすると、
問題4
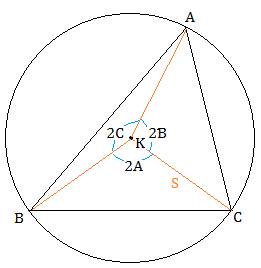
外心は外接円の中心です。
円周角と中心角との関係から、
∠BKC＝2A、∠CKA＝2B、∠AKB＝2C
外心から各頂点までの距離Sが等しいので、
なので、
△KBC：△KCA：△KAB＝sin2A：sin2B：sin2C です。
問題1のp＝sin2A、q＝sin2B、r＝sin2Cとすると、
問題5
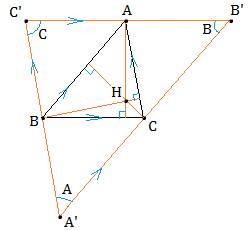
各頂点から対辺に平行な線を引くことでできる三角形を
A’B’C’とします。
□ABA’C、□BCB’A、□CAC’Bは平行四辺形です。
平行四辺形の対辺の長さは等しいです。
よって、△A’B’C’の外心と△ABCの垂心とは同じ点です。
同様に、
ここで、
の係数を調べます。
、
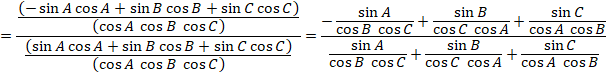
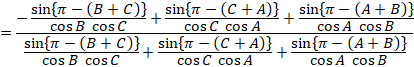
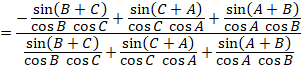
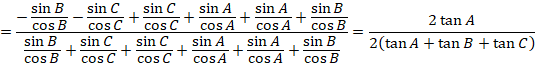
の係数も同様に、
よって、
問題6
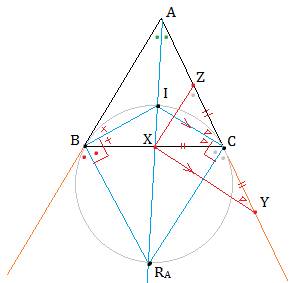内心をI、傍心をRAとします。
∠Aの二等分線と底辺BCとの交点をXとします。
ACの延長上にCX＝CYとなる点Yをとります。
すると、△CXYは二等辺三角形です。
この二等辺三角形の底角の和は、∠ACXと等しいので、
ICとXYは平行になります。
△ACI∽△AYXです。
AI：IX＝AC：CY＝AC：CX ･･････ (3)
AC上にCX＝CZとなる点Zをとります。
すると、△CZXは二等辺三角形です。
この二等辺三角形の底角の和は、∠XCYと等しいので、ZXとCRAは平行になります。
△AZX∽△ACRAです。
ARA：RAX＝AC：CZ＝AC：CX ･･････ (4)
(2) と(4)から
Iは線分AXをAC：CXに内分する点、
RAは線分AXをAC：CXに外分する点となります。
よって、点Cは線分IRAを直径とするアポロニウスの円上にあります。
（∠ICRA＝∠R です）
∠Aの二等分線上にXがあるので、BX：XC＝c：b です。
すると、
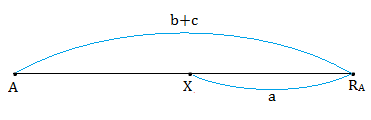
よって、
NO2「三角定規」
02/24 22時57分 受信 更新 3/17
NO3「浜田明巳」 03/08 11時38分 受信 更新 3/17
原点をＯとする．
文字の誤用を避ける為に，
ＢＣ＝ｓ，ＣＡ＝ｔ，ＡＢ＝ｕ，
ﾍﾞｸﾄﾙａ＝ａ，ﾍﾞｸﾄﾙｂ＝ｂ，ﾍﾞｸﾄﾙｃ＝ｃ，ﾍﾞｸﾄﾙｇ＝ｇ，ﾍﾞｸﾄﾙｉ＝ｉ，ﾍﾞｸﾄﾙｋ＝ｋ，
ﾍﾞｸﾄﾙｈ＝ｈ，ﾍﾞｸﾄﾙｒＡ＝ｒＡ，ﾍﾞｸﾄﾙｐ＝ｎ
と表記する（本当はベクトル記号がうまく書けないだけ）．
問題１
ＡＰとＢＣの交点をＤとすると，
ＢＤ：ＤＣ＝△ＡＢＤ：△ＡＣＤ＝△ＰＡＢ：△ＰＣＡ＝ｒ：ｑ
∴ﾍﾞｸﾄﾙＯＤ＝(ｑｂ＋ｒｃ)／(ｒ＋ｑ)＝(ｑｂ＋ｒｃ)／(ｑ＋ｒ)
また，
ＡＰ：ＰＤ＝(△ＰＡＢ＋△ＰＣＡ)：△ＰＢＣ＝(ｒ＋ｑ)：ｐ
∴ｎ＝{ｐａ＋(ｑ＋ｒ)・ﾍﾞｸﾄﾙＯＤ}／{(ｑ＋ｒ)＋ｐ}
＝{ｐａ＋(ｑ＋ｒ)・(ｑｂ＋ｒｃ)／(ｑ＋ｒ)}／(ｐ＋ｑ＋ｒ)
＝(ｐａ＋ｑｂ＋ｒｃ)／(ｐ＋ｑ＋ｒ)
問題２
ＢＣの中点をＭとすると，ﾍﾞｸﾄﾙＯＭ＝(ｂ＋ｃ)／２
また，Ｇは△ＡＢＣの重心なので，ＡＧ：ＧＭ＝２：１
ｇ＝(１・ａ＋２・ﾍﾞｸﾄﾙＯＭ)／(２＋１)＝{ａ＋２・(ｂ＋ｃ)／２}／３
＝(ａ＋ｂ＋ｃ)／３
問題３
ＡＩとＢＣの交点をＤとする．
ＡＩは∠ＢＡＣの二等分線なので，
ＢＤ：ＤＣ＝ＡＢ：ＡＣ＝ｕ：ｔ
∴ﾍﾞｸﾄﾙＯＤ＝(ｔｂ＋ｕｃ)／(ｕ＋ｔ)＝(ｔｂ＋ｕｃ)／(ｔ＋ｕ)
また，△ＡＢＤにおいて，ＢＩは∠ＡＢＤの二等分線なので，
ＡＩ：ＩＤ＝ＡＢ：ＢＤ＝ｕ：{ｕ／(ｕ＋ｔ)・ｓ}＝(ｔ＋ｕ)：ｓ
∴ｉ＝{ｓａ＋(ｔ＋ｕ)・ﾍﾞｸﾄﾙＯＤ}／{(ｔ＋ｕ)＋ｓ}
＝{ｓａ＋(ｔ＋ｕ)・(ｔｂ＋ｕｃ)／(ｔ＋ｕ)}／(ｓ＋ｔ＋ｕ)
＝(ｓａ＋ｔｂ＋ｕｃ)／(ｓ＋ｔ＋ｕ)
問題４
外接円の半径を，ＡＫ＝ＢＫ＝ＣＫ＝Ｒとする．
i). △ＡＢＣが鋭角三角形のとき，外心Ｋは△ＡＢＣの内部にあり，
△ＫＢＣ＝１／２・ＫＢ・ＫＣ・sin２Ａ＝Ｒ２／２・sin２Ａ
△ＫＣＡ＝Ｒ２／２・sin２Ｂ
△ＫＡＢ＝Ｒ２／２・sin２Ｃ
∴△ＫＢＣ：△ＫＣＡ：△ＫＡＢ＝sin２Ａ：sin２Ｂ：sin２Ｃ
問題１と同様に，
ｋ＝(sin２Ａ・ａ＋sin２Ｂ・ｂ＋sin２Ｃ・ｃ)／(sin２Ａ＋sin２Ｂ＋sin２Ｃ)
ii). ∠Ａ＝π／２のとき，外心Ｋは斜辺ＢＣの中点であるので，
ｋ＝(ｂ＋ｃ)／２
また，
sin２Ａ＝sin(２・π／２)＝０
sin２Ｃ＝sin２(π／２−∠Ｂ)＝sin(π−２∠Ｂ)＝sin２Ｂ≠０
∴ｋ＝(sin２Ａ・ａ＋sin２Ｂ・ｂ＋sin２Ｃ・ｃ)／(sin２Ａ＋sin２Ｂ＋sin２Ｃ)
他の頂角が直角でも同様に成立する．
iii). ∠Ａ＞π／２のとき，外心Ｋは△ＡＢＣの外部にあり，線分ＡＫは辺ＢＣと交わり，交点をＤとする．
△ＫＢＣ：△ＫＣＡ：△ＫＡＢ＝ｐ：ｑ：ｒとする．
ＢＤ：ＤＣ＝△ＫＡＢ：△ＫＣＡ＝ｒ：ｑ
から，
ﾍﾞｸﾄﾙＯＤ＝(ｑｂ＋ｒｃ)／(ｒ＋ｑ)
ＫはＡＤを，
ＡＫ：ＫＤ＝(△ＫＡＢ＋△ＫＣＡ)：△ＫＢＣ＝(ｒ＋ｑ)：ｐ
に外分しているので，
ｋ＝{−ｐａ＋(ｑ＋ｒ)・ﾍﾞｸﾄﾙＯＤ}／{(ｑ＋ｒ)−ｐ}＝(−ｐａ＋ｑｂ＋ｒｃ)／(−ｐ＋ｑ＋ｒ)
ここで，
△ＫＢＣ＝Ｒ２／２・sin(２π−２∠Ａ)＝Ｒ２／２・(−sin２Ａ)，
△ＫＣＡ＝Ｒ２／２・sin２Ｂ，△ＫＡＢ＝Ｒ２／２・sin２Ｃ
∴ｐ：ｑ：ｒ＝(−sin２Ａ)：sin２Ｂ：sin２Ｃ
∴ｋ＝(sin２Ａ・ａ＋sin２Ｂ・ｂ＋sin２Ｃ・ｃ)／(sin２Ａ＋sin２Ｂ＋sin２Ｃ)
他の頂角が鈍角でも同様に成立する．
問題５
i). △ＡＢＣが鋭角三角形のとき，垂心Ｈは△ＡＢＣの内部にある．
ＡＨとＢＣの交点をＤとすると，
△ＨＡＢ：△ＨＣＡ＝ＢＤ：ＤＣ＝(ＡＤ／tanＢ)：(ＡＤ／tanＣ)＝tanＣ：tanＢ
同様に，
△ＨＡＢ：△ＨＢＣ＝tanＣ：tanＡ
∴△ＨＢＣ：△ＨＣＡ：△ＨＡＢ＝tanＡ：tanＢ：tanＣ
問題１と同様に，
ｈ＝(tanＡ・ａ＋tanＢ・ｂ＋tanＣ・ｃ)／(tanＡ＋tanＢ＋tanＣ)
ii). ∠Ａ＝π／２のとき，垂心ＨはＡとなる．
∠Ａ→π／２±０で考える．
(tanＡ・ａ＋tanＢ・ｂ＋tanＣ・ｃ)／(tanＡ＋tanＢ＋tanＣ)
＝(ａ＋tanＢ／tanＡ・ｂ＋tanＣ／tanＡ・ｃ)／(１＋tanＢ／tanＡ＋tanＣ／tanＡ)
→ａ（∠Ａ→π／２±０）
＝ｈ
故に成立する．他の頂角がπ／２でも同様に成立する．
（総合学習で扱う問題であるから，ここまでやった方がよいでしょう）
iii). ∠Ａ＞π／２のとき，ＡＨとＢＣの交点をＤとする．
△ＨＢＣ：△ＨＣＡ：△ＨＡＢ＝ｐ：ｑ：ｒとする．
ＢＤ：ＤＣ＝△ＨＡＢ：△ＨＣＡ＝ｒ：ｑ
から，
ﾍﾞｸﾄﾙＯＤ＝(ｑｂ＋ｒｃ)／(ｒ＋ｑ)
ＨはＡＤを，
ＡＨ：ＨＤ＝(△ＨＡＢ＋△ＨＣＡ)：△ＨＢＣ＝(ｒ＋ｑ)：ｐ
に外分しているので，
ｈ＝{−ｐａ＋(ｒ＋ｑ)・ﾍﾞｸﾄﾙＯＤ}／{(ｒ＋ｑ)−ｐ}＝(−ｐａ＋ｑｂ＋ｒｃ)／(−ｐ＋ｑ＋ｒ)
ここで，
△ＨＡＢ：△ＨＣＡ＝ＢＤ：ＤＣ＝(ＡＤ／ＤＣ)：(ＡＤ／ＢＤ)＝tanＣ：tanＢ
ＡＢとＣＨの交点をＥとすると，
△ＨＢＣ：△ＨＣＡ＝ＢＥ：ＡＥ＝(ＣＥ／ＡＥ)：(ＣＥ／ＢＥ)＝tan∠ＣＡＥ：tanＢ
＝tan(π−∠Ａ)：tanＢ＝(−tanＡ)：tanＢ
∴△ＨＢＣ：△ＨＣＡ：△ＨＡＢ＝(−tanＡ)：tanＢ：tanＣ
∴ｈ＝(tanＡ・ａ＋tanＢ・ｂ＋tanＣ・ｃ)／(tanＡ＋tanＢ＋tanＣ)
他の頂角が鈍角でも同様に成立する．
問題６
ＡＲＡとＢＣの交点をＤとすると，
ＢＤ：ＤＣ＝ＡＢ：ＡＣ＝ｕ：ｔ
∴ﾍﾞｸﾄﾙＯＤ＝(ｔｂ＋ｕｃ)／(ｕ＋ｔ)
Ｄを通り,ＢＲＡと平行な直線とＡＢの交点をＥ，直線ＡＢと傍心円ＲＡの接点をＦとする．
ＥＤ//ＢＲＡより，錯角，同位角が等しいので，
∠ＢＤＥ＝∠ＤＢＲＡ
∠ＢＥＤ＝∠ＦＢＲＡ＝∠ＤＢＲＡ
∴∠ＢＤＥ＝∠ＢＥＤ
∴ＢＤ＝ＢＥ
∴ＡＲＡ：ＲＡＤ＝ＡＢ：ＢＥ＝ＡＢ：ＢＤ＝ｕ：{ｕ／(ｕ＋ｔ)・ｓ}＝(ｕ＋ｔ)：ｓ
∴ｒＡ＝{−ｓａ＋(ｕ＋ｔ)・ﾍﾞｸﾄﾙＯＤ}／{(ｕ＋ｔ)−ｓ}＝(−ｓａ＋ｔｂ＋ｕｃ)／(−ｓ＋ｔ＋ｕ)
（この場合分けの多さは，集中力がない私にはきつかったです）
＜水の流れから＞
当時、実教出版から出ていた数学資料NO63（2011年10月発行）の中にあった証明を載せておきます。追加の「フェルマー点」のベクトル表示は興味深いです。皆さん、是非参考にしてください。
