平成３１年３月１７日

[流れ星]

　　　　第371回数学的な応募問題

　　　　＜解答募集期間：３月17日〜４月14日＞

［ひし形の面積］

　円に内接する四角形ＡＢＣＤの２組の対辺のなす∠ＢＥＣとＡＦＢとし、
それぞれの角の２等分線を図のようにＥＩＧとＦＨＪとする。
ただし、点Ｇ，Ｈ，Ｉ、Ｊは四角形ＡＢＣＤの辺上にある。次の問に答えよ。

　

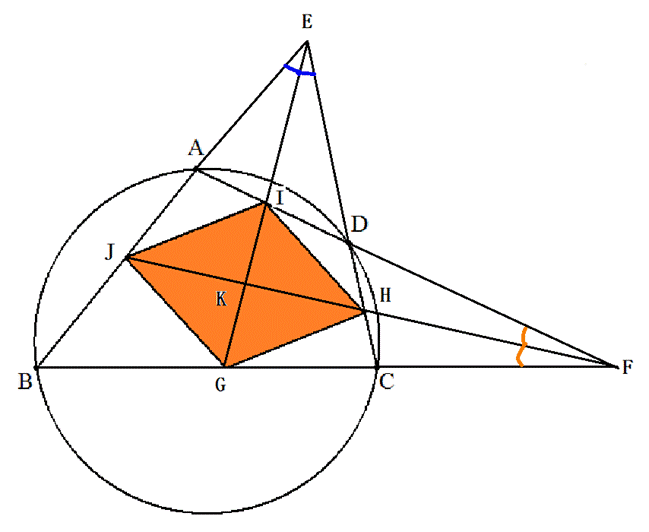
　ここで、四角形ＧＨＩＪの対角線の交点をＫとする。

問１　四角形ＧＨＩＪはひし形になることを証明せよ。

問２　三角形ＡＥＤで、ＥＩ^２＝ＡＥ・ＥＤ−ＡＩ・ＩＤを証明せよ。

　　　ヒント　角の２等分線の定理も使う。

ここから、辺の長さをＡＢ＝４、ＢＣ＝６、ＣＤ＝２、ＤＡ＝３とする。

問３　線分ＥＡ，ＥＤ、ＦＤ，ＦＣの長さを求めよ。

問４　線分ＥＩ、ＥＧ、ＦＨ，ＦＪの長さを求めよ。

問５　ひし形ＧＨＩＪの面積を求めよ。

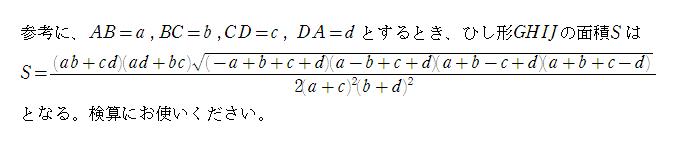
出典　時岡郁夫さんのHPにある「こだわり数学」から　

７２円に内接する四角形に内接するひし形について

追加日　令和元年10月21日　20時　

＜水の流れ：出典先を明記せずに大変ご迷惑をおかけしたことにお詫び致します。＞

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。