平成３１年４月１4丁目日

[流れ星]

　　　　第371回数学的な応募解答

　　　　＜解答募集期間：３月17日〜４月14日＞

［ひし形の面積］

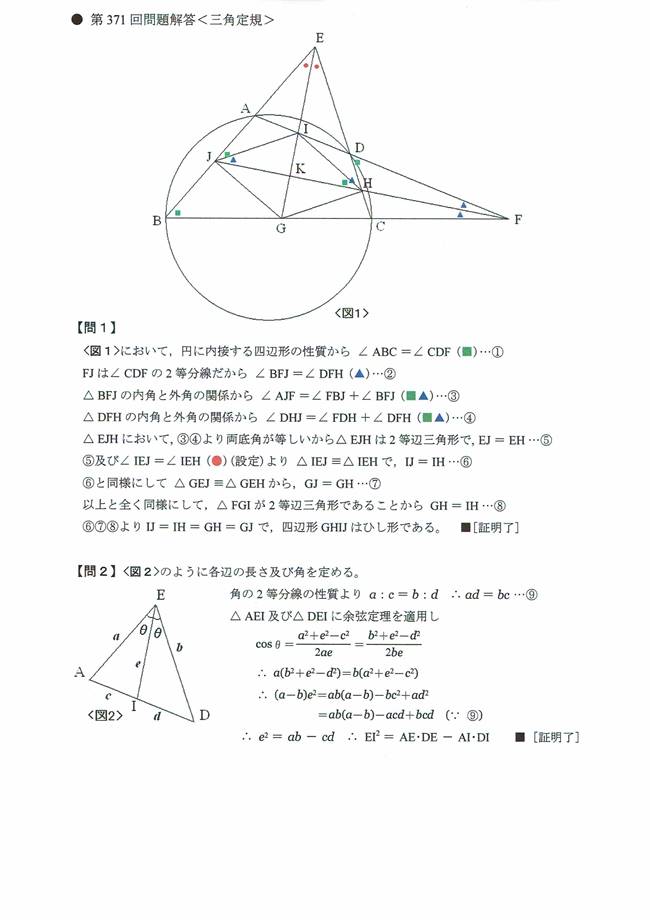
　円に内接する四角形ＡＢＣＤの２組の対辺のなす∠ＢＥＣとＡＦＢとし、
それぞれの角の２等分線を図のようにＥＩＧとＦＨＪとする。
ただし、点Ｇ，Ｈ，Ｉ、Ｊは四角形ＡＢＣＤの辺上にある。次の問に答えよ。

　

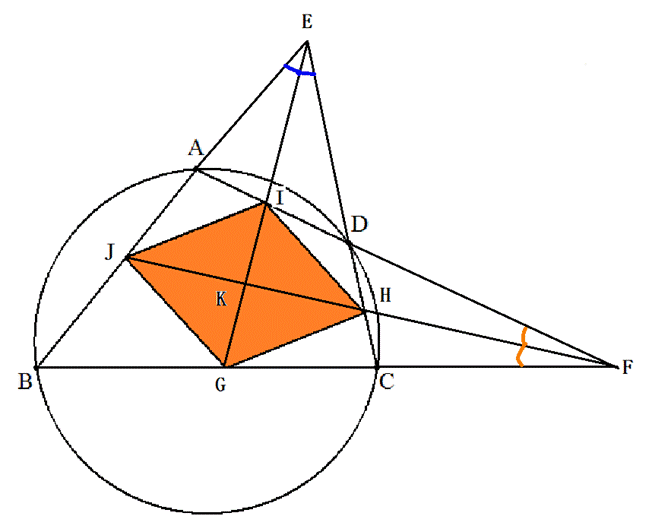
　ここで、四角形ＧＨＩＪの対角線の交点をＫとする。

問１　四角形ＧＨＩＪはひし形になることを証明せよ。

問２　三角形ＡＥＤで、ＥＩ^２＝ＡＥ・ＥＤ−ＡＩ・ＩＤを証明せよ。

　　　ヒント　角の２等分線の定理も使う。

ここから、辺の長さをＡＢ＝４、ＢＣ＝６、ＣＤ＝２、ＤＡ＝３とする。

問３　線分ＥＡ，ＥＤ、ＦＤ，ＦＣの長さを求めよ。

問４　線分ＥＩ、ＥＧ、ＦＨ，ＦＪの長さを求めよ。

問５　ひし形ＧＨＩＪの面積を求めよ。

＜水の流れ＞参考にした「数学のいずみ」数学教育実践研究会サイトです。

出典　時岡郁夫さんのHPにある「こだわり数学」から　

７２円に内接する四角形に内接するひし形について

追加日　令和元年10月21日　20時　

＜水の流れ：出典先を明記せずに大変ご迷惑をおかけしたことにお詫び致します。＞

NO1「早起きのおじさん」 03/20 22時13分　受信 更新

「早起きのおじさん」 03/27 18時09分　受信 更新 4/14

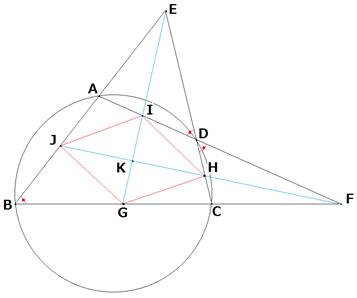問1

四角形ABCDの内角の大きさをそれぞれA、B、C、Dで表すことにします。

円に内接する四角形の向かい合う内角の和はそれぞれπです。

　B＋D＝π　･･･　�@

四角形ABCDの角Dの2つの外角（∠CDF、∠ADE）の大きさはともにBです。

四角形BFDEの頂点F、Eの内角の大きさをそれぞれF、Eで表すことにします。

四角形BFDEの頂点Dの内角の大きさは、2B＋Dです。

四角形BFDEの内角の和は2πです。

　B＋F＋(2B＋D)＋E＝2π

�@を代入して、

　2B＋F＋E＝π

　(B＋F／2＋E／2＝π／2)　･･･　�A

四角形KHDIの頂点Kの内角の大きさをKとします。

四角形KHDIの頂点H、Iの内角の大きさは、それぞれB＋F／2、B＋E／2です。

四角形KHDIの内角の和は2πです。

　K＋(B＋F／2)＋D＋(B＋E／2)＝2π

�@を代入して、

K＋B＋F／2＋E／2＝π

�Aを代入して、

K＝π／2

よって、四角形GHIJの対角線は、直交しています。

さて、△EJHは、△EJK≡△EHK（二角夾辺）となるので、二等辺三角形です。

よって、△IJHも二等辺三角形になるので、IJ＝IHです。

同様に、△FIGも二等辺三角形になるので、△HIGも二等辺三角形です。

よって、HI＝HGです。

△IJK≡△IHK、△IHK≡△GHKなので、△GJKもこれらの三角形と合同です。

よって、四角形GHIJの4つの辺の長さが等しくなります。

以上から、四角形GHIJはひし形です。

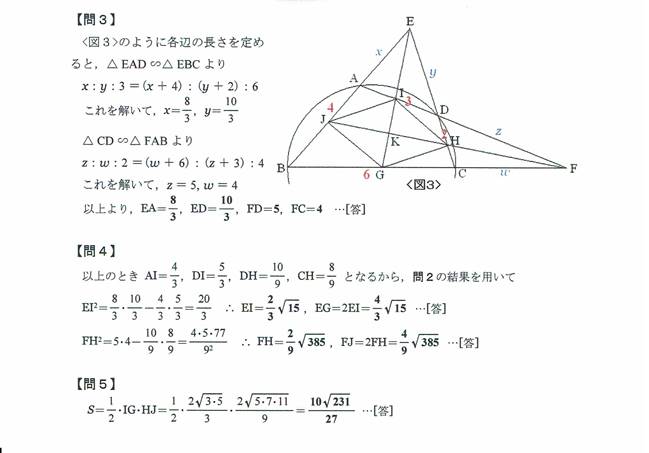
問2

∠AEDの大きさを2θとします。

△EAI、△EDIに余弦定理をもちいると、

AI²＝EA²＋EI²−2EA･EIcosθ　･･･　�B

DI²＝ED²＋EI²−2ED･EIcosθ　･･･　�C

�B、�Cからθを消去すると（�B×ED−�C×EA）、

ED･AI²−EA･DI²＝ED･(EA²＋EI²)−EA･(ED²＋EI²)

EI²(ED−EA)＝EA･ED²−ED･EA²−EA･DI²＋ED･AI²　･･･　�D

さて、△EADにおいて、EIが角の2等分線なので、

　EA：ED＝AI：ID

よって、EA･ID＝ED･AI

この式を用いると、�Dは、

EI²(ED−EA)＝EA･ED²−ED･EA²−EA･DI²＋ED･AI²

　　　　　 ＝AE･ED･ED−AE･ED･EA−EA･ID･ID＋ED･AI･AI

　　　　　 ＝AE･ED(ED−EA)−ED･AI･ID＋EA･ID･AI

　　　　　 ＝AE･ED(ED−EA)−AI･ID(ED−EA)

よって、

EI²＝AE･ED−AI･ID

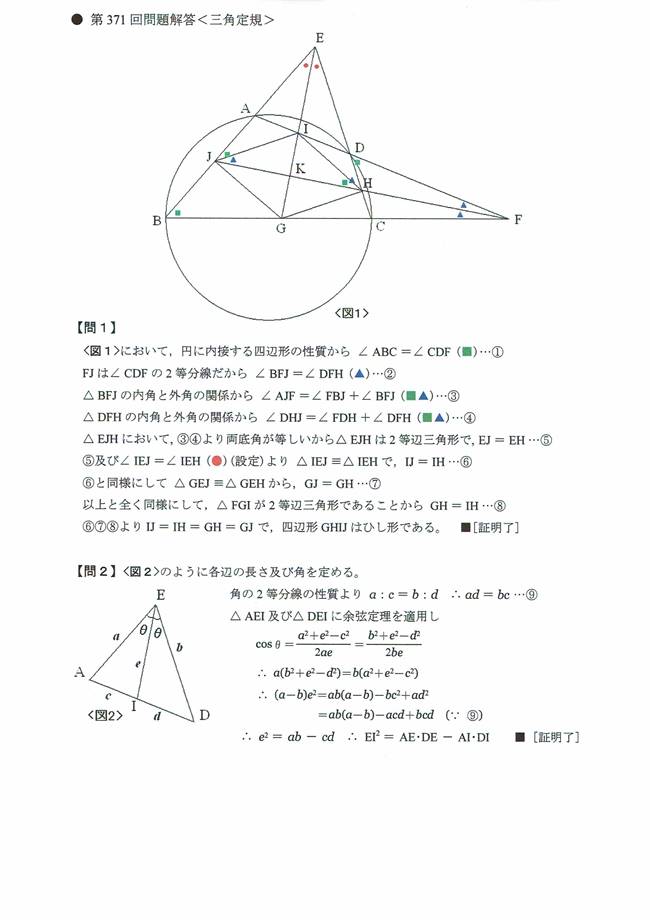
問3

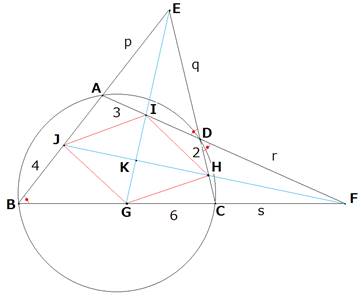EA＝p、ED＝q、FD＝r、FC＝sとおきます。

△EAD∽△ECBなので、

　EA：AD＝EC：CB

　ED：DA＝EB：BC

つまり、

　p：3＝(q＋2)：6

　q：3＝(p＋4)：6

上の式より、q＝2p−2

下の式に入れて、p＝EA＝8／3

よって、q＝ED＝10／3

同様に、△FDC∽△FBAなので、

　FD：DC＝FB：BA

　FC：CD＝FA：AB

つまり、

　r：2＝(s＋6)：4

　s：2＝(r＋3)：4

上の式より、s＝2r−6

下の式に入れて、r＝FD＝5

よって、s＝FC＝4

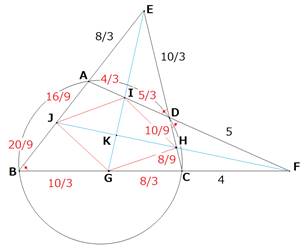問4

EA：ED＝4：5、FC：FD＝4：5なので、

AI＝4／3、ID＝5／3、CH＝8／9、HD＝10／9

CG＝8／3、GB＝10／3、AJ＝16／9、JB＝20／9

問2の結果より、

△AED∽△CEBでAD：CB＝3：6

同様に、

△CFD∽△AFBでCD：AB＝2：4

問5

以上から、ひし形GHIJの対角線の長さは、

よって、ひし形GHIJの面積Sは、

●おまけ

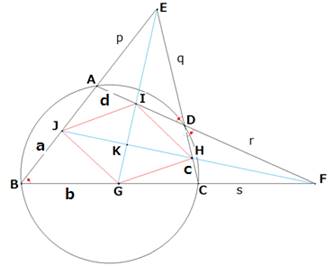ひし形GHIJの面積を一般的に調べてみます。

○p、q、r、sを求めます。

より、

より、

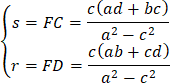
○AI、ID、CH、HDを求めます。

○EC、EB、FA、FBを求めます。

○CG、GB、AJ,JBを求めます。

○ を調べます。

○IG、HJを調べます。

○ひし形の面積を求めます。

37１解答　早起きのおじさん

●おまけ2

ひし形GHIJの面積を一般的に調べてみます。

次の流れで考えます。

・□ABCDの面積

・△FABの面積

・△FAJ、△FBJの面積

・△FAJ　→　△FIJ　→　△IJH

　△FBJ　→　△FGJ　→　△GJH

・ひし形IJGHの面積

○□ABCD＝Sとおきます。

Sは、No366の問題のときに計算した結果を使います。

○△FABの面積は、△FCDと△FABが相似なので、

△FCD＝X、△FAB＝Yとおくと、

○おまけの結果から、

なので、

よって、△FAJと△FBJは、

○おまけの結果から、

なので、

また、

よって、

一方、おまけの結果から、

(△FIGは二等辺三角形です)

なので、

また、

よって、

(△IJH≡△GJHは合同です)

○以上から、ひし形GHIJは、

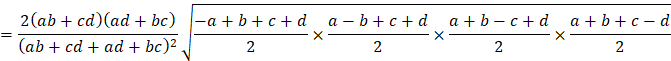
NO2「三角定規」 03/24 13時56分　受信 更新 4/14

NO3「スモークマン」 03/31 18時00分　受信 更新 4/14

久しぶりにチャレンジ〜!!

こちらは、今週、さくら開花しそうです🌸

問１　四角形ＧＨＩＪはひし形になることを証明せよ。

回答

△EAI〜△ECG

so...

角EIA=角EGC=角FGI

また、明らかに、角EIA=角FIG

so...

△FIGは二等辺三角形

so...FG垂直IG

同様に、△AJHも二等辺三角形で、EK垂直JH

so...対角線が互いに直行して二等分されているので、資格GHIJはひし形 ^^

問２　三角形ＡＥＤで、ＥＩ^２＝ＡＥ・ＥＤ−ＡＩ・ＩＤを証明せよ。

　　　

回答

天下り的に...

http://examist.jp/mathematics/math-1/trigonometric-ratio/nitoubunsen-nagasa/

に示されている図添付 Orz...

ここから、辺の長さをＡＢ＝４、ＢＣ＝６、ＣＤ＝２、ＤＡ＝３とする。

問３　線分ＥＡ，ＥＤ、ＦＤ，ＦＣの長さを求めよ。

回答

△AEDと△ACBとの辺の長さの相似比は1:2

so...EA=x,ED=y

2^2*xy=(x+4)(y+2)・・・3xy=4y+2x+8

また、(y+2)/x=(x+4)/y=2

so...3x*(x+4)/2=2(x+4)+2x+8=4x+16

3x(x+4)=8x+32

3x^2+4x-32=(x+4)(3x-8)=0

x=EA=x=8/3,ED=y=10/3

2^2*zw=(z+3)(w+6)

(z+3)/w=(w+6)/z=2

3zw=6z+3w+18

3z*(z+3)/2=6z+3(z+3)/2+18

3z(z+3)=12z+3(z+3)+36

z^2-2z-15=(z+3)(z-5)=0

FD=z=5,FC=w=4

問４　線分ＥＩ、ＥＧ、ＦＨ，ＦＪの長さを求めよ。

回答

EI

=√(EA*ED-AI*ID)

=√(8*10/3^2-3^2*4*5/9^2)

=√(8*10-4*5)/3

=2√15/3

EG=4√15/3

FH

=√(FD*FC-DH*HC)

=√(5*4-2^2*5*4/9^2)

=√(20*(1-4/81))

=2√385/9

FJ=4√385/9

問５　ひし形ＧＨＩＪの面積を求めよ。

ひし形IJGH

=IG*JH/2

=(2√15/3)(2√385/9)/2

=10√231/27

*検算...でも、

((4*6+2*3)(4*3+6*2)*√((-4+6+2+3)(4-6+2+3)(4+6-2+3)(4+6+2-3)))/(2(4+2)^2*(6+3)^2)

=10√231/27 ♪

NO4「にいばりZ12」　　　04/04 01時18分　受信 更新 4/14

円に内接する四角形ＡＢＣＤの２組の対辺のなす∠ＢＥＣとＡＦＢとし、
それぞれの角の２等分線を図のようにＥＩＧとＦＨＪとする。
ただし、点Ｇ，Ｈ，Ｉ、Ｊは四角形ＡＢＣＤの辺上にある。次の問に答えよ。

ここで、四角形ＧＨＩＪの対角線の交点をＫとする。

問１　四角形ＧＨＩＪはひし形になることを証明せよ。

　いま直線EKをｙ軸、FKをｘ軸にとります

　また、∠BEC＝α、∠AFB＝βとします

　さらに∠ADC=θ₁、∠ABC＝θ₂とします

　Dからx,y軸に垂線の足を下しその交点を各々P₁,Q₁とします。

　同様に

　Bからx,y軸に垂線の足を下しその交点を各々P₂,Q₂とします。

　∠IDQ₁＝β/2、∠HDP₁＝α/2

　∠JBQ₂＝β/2、∠HDP₂＝α/2

そうすると

　θ₁＝∠R+（α+β）/2

　θ₂＝∠R-（α+β）/2

　θ₁+θ₂＝2∠R

今、x[軸とy軸が直交していないと

θ₁+θ₂≠2∠R

　となり四角形ABCDは円に内接しません。

　よって

　

　∠EKH=∠R

△EJKと△EHKはEKを共有し3角が等しいので合同

　△IHKと△GHKはHKを共有し3角が等しいので合同

△HGKと△JGKはGKを共有し3角が等しいので合同

以上から四角形IJGHは菱形である・・・・回答

問2　三角形ＡＥＤで、ＥＩ^２＝ＡＥ・ＥＤ−ＡＩ・ＩＤを証明せよ。

　　　ヒント　角の２等分線の定理も使う。

角の２等分線の定理から解く方法が解りませんでしたので取りあえず別解を考えました。

　

△AEDに外接する円を考え、直線EIとのEではない交点をMとします。

円周角の定理（∠EMA＝∠EDA）から

△EMA∽△EDI

EM：EA＝ED：EI

EM・EI＝EA・ED

EM=EI+IMなので

（EI+IM）・EI＝EA・ED

EI²+IM・EI＝EA・ED

EI²＝EA・ED−IM・EI・・・�@

さらに

円周角の定理（∠EDA＝∠EMA）から

△AIM∽△EID

EI：AI＝ID：IM

EI・IM＝AI・ID

なので�@は

EI²＝EA・ED−AI・ID・・・回答

ここから、辺の長さをＡＢ＝４、ＢＣ＝６、ＣＤ＝２、ＤＡ＝３とする。

問３　線分ＥＡ，ＥＤ、ＦＤ，ＦＣの長さを求めよ。

問1より∠EKF＝∠R

　よって

　△EAD∽ECB

　上記三角形の辺の比はAD：CB＝3：6＝1：2

　ED：EB＝1：2　　

ED：（EA+4）＝1：2

　EA：EC＝1：2

　　　EA：（ED+2）＝1：2

　　これを連立して解くと

　　EA=8/3、ED=10/3

また同様に

△FCD∽FAB

　上記三角形の辺の比はCD：AB＝2：4＝1：2

　FC：FA＝1：2　　

FC：（FD+3）＝1：2

　FD：FB＝1：2

　　　FD：（FC+6）＝1：2

　　これを連立して解くと

　　FD＝5、FC＝4

　以上から

　　EA＝8/3

　　ED＝10/3

　　FD＝5

　　FC＝4　　　・・・・回答

問４　線分ＥＩ、ＥＧ、ＦＨ，ＦＪの長さを求めよ。

問2から

EI²＝EA・ED−AI・ID

また、角の2等分線定理から

ED・AI＝AE・ID

　　10/3・AI＝8/3・ID

　　AI＝4/5・ID

EI²＝8/3・10/3−AI・ID

AD＝3＝AI+ID

　　ID＝3−AI

＝3−4/5・ID

　　ID＝5/3

　　AI=3−ID=3−5/3＝4/3

EI²＝8/3・10/3−4/3・5/3＝60/9

△EAI∽△ECG、△EDI∽△EBEで辺の比は1：2

∴EG²＝4・60/9＝240/9

同様に

FH²＝5・4−DH・CH＝5・4−10/9・8/9＝1540/81

（DH＝5/4・CH、CH=2−DH                

DH=5/4・（2−DH）

DH=4/9・10/4＝10/9

CH＝2-10/9＝8/9）

△FDH∽△FBJ、△FCH∽△FAJで辺の比は1：2

∴FJ²＝4・1540/81＝6160/81

以上から

EI＝60^1/2/3　　　＝2・15^1/2/3

EG＝240^1/2/3　　＝4・15^1/2/3

FH＝1540^1/2/9　　＝2・385^1/2/9

FJ＝6160^1/2/9  　＝4・385^1/2/9・・・・回答

問５　ひし形ＧＨＩＪの面積を求めよ。

菱形の面積は

S＝（EG−EI）・（FJ−FH）/2

なので問4から

S＝（2・15^1/2/3）・（2・385^1/2/9）/2＝10√231/27・・・回答(5.629142279)

検算

              a            =AB=4                 

              b            =BC=6                 

              c            =CD=2                 

              d            =DA=3                 

1）         (ab+cd)(ad+bc)＝ 720                       �@

2）         2s=(a+b+c+d)                                                

　　　　　 s=(a+b+c+d)/2＝7.5                  

              (-a+b+c+d)                                                     

              =2(s-a)                                             

                            s-a＝3.5                       �A

              (a-b+c+d)                                                       

              =2(s-b)                                             

                            s-b＝1.5                       �B

              (a+b-c+d)                                                       

              =2(s-b)                                             

                            s-c＝5.5                       �C

              (a+b+c-d)                                                       

              =2(s-b)                                             

                            s-d＝4.5                  �D

              ((-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d))^1/2

              =4((s-a)(s-b)(s-c)(s-d))^1/2

　　　　　　　2(�A�B�C�D)^1/2＝22.79802623   �E

3）         2(a+c)2(b+d)2                                                

　　　　　　　　　　(a+c)²(b+d)²＝2916       �F

菱形の面積 　　　　　　　　　S＝�@*�E/�F＝5.629142279                       ok !