2019�N�ߘa���N5���P2��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��372�����w�I�ȉ����
�@�@�@�@����W���ԁF4��14���`5��12����
�m�����Ɩʐς������}�`�n
�@2018�N9��19�����V�����u�ӂ̒��������ׂĐ����ƂȂ钼�p�O�p�`�ƓӎO�p�`�̑g�̒��ɂ́A���̒������ʐς����ɓ������g���i�����������āj������1�g�����Ȃ��v���Ƃ��ؖ������������L�����ڂ��Ă��܂����B���̑g�ݍ��킹�́A�O�ӂ��u135�A352�A377�v�̒��p�O�p�`�Ɓu132�A366�A366�v�̓ӎO�p�`�������ł��B���̒�����864�A�ʐς�23760�ɂȂ�܂��B���̖��̗ޑ�ł��B
���镽�ʐ}�`�ɂ����āA�ӂ̒��������ׂĐ����ŁA���̒����Ɩʐς��������ʑ��p�`���l���܂��B
���P�@����}�`�������`�i�����`���܂ށj�ł���Ƃ��A����������Ȃ����B
�@�@�@�@�i�Q����܂��j
���Q�@����}�`���ӎO�p�`�i���O�p�`���܂ށj�ł���Ƃ��A���݂��Ȃ����Ƃ������Ȃ����B
���R�@����}�`���O�p�`�̂Ƃ��A����������Ȃ����B�i�T����܂��j
���̑O�ɁA�s��������@���������S�i���{���{���j�̐��̐����������߂Ă����Ă��������B
���S�@����}�`�����s�l�ӌ`��Ђ��`�̂Ƃ��A���݂��邩�ǂ����l�@���Ă݂Ă��������B
NO1�u�X���[�N�}���v 04/16
18��14���@��M �X�V 5/12
������`�������W����...but...�悭�Ӗ������߂Ȃ�����...^^;
�����̗���F�o��҂̈Ӑ}�ƈႤ���߂��ł���悤�ȂƂ��́A�\����Ȃ��ł���
���镽�ʐ}�`�ɂ����āA�ӂ̒��������ׂĐ����ŁA���̒����Ɩʐς��������ʑ��p�`���l���܂��B
���P�@����}�`�������`�i�����`���܂ށj�ł���Ƃ��A����������Ȃ����B�i�Q����܂��j
��
�����`��2�ӂ̒�����a,b�Ƃ����
ab=2(a+b)
(a-2)(b-2)=4
a-2=1,b-2=4�E�E�E(a,b)=(3.6)
a-2=2,b-2=2�E�E�E(a,b)=(4,4)
���Q�@����}�`���ӎO�p�`�i���O�p�`���܂ށj�ł���Ƃ��A���݂��Ȃ����Ƃ������Ȃ����B
��
�ӎO�p�`�ȊO�́��̑��݂͍ŏ��ɑ��݂�������Ă���̂ŁA
���̑�ӂ�ӎO�p�`�Ɠ��������`���Ȃ����Ƃ������̂��낤���ƁH
���1����A3*6=18
c^2*sin��=2*18
2c+��(2*c^2*��(1-(sin��)^2))=18
PC�Łcc=6.249�c
4*4=16
c^2*sin��=2*16
2c+��(2*c^2*��(1-(sin��)^2))=16
c=5.785�c
�Ŗ������Ȃ��c
���R�@����}�`���O�p�`�̂Ƃ��A����������Ȃ����B�i�T����܂��j
���̑O�ɁA�s��������@���������S�i���{���{���j�̐��̐����������߂Ă����Ă��������B
��
AB=a,BC=b,CA=c
a+b+c=2s
S=��(s(s-a)(s-b)(s-c))=a+b+c
S^2=
s(s-a)(s-b)(s-c)=(a+b+c)^2=4s^2
(s-a)(s-b)(s-c)=4s=2(a+b+c)
s-a=x,s-b=y,s-c=z
x+y+z=3s-2s=s
xyz=4(x+y+z)
1/4=1/xy+1/yz+1/zx
x<=y<=z
1/4<=3/x^2
So�cx^2<=12
So�cx=1,2,3
x=1�c
1/4=1/y+1/yz+1/z
1/4<=2/y+1/y^2
y^2-8y<=4
y(y-8)<=4�cy=(1,2,3,4),5,6,7,8
y=5�c
1/4=1/5+1/(5z)+1/z
5z=4z+4+20�cz=24
y=6�c
1/4=1/6+1/(6z)+1/z
6z=4z+4+24�cz=14
y=7�c
1/4=1/7+1/(7z)+1/z
7z=4z+4+28�cz=32/3�łȂ�
y=8�c
1/4=1/8+1/(8z)+1/z
8z=4z+4+32�cz=9
x=2�c
1/4<=1/y+1/y^2
y^2-4y=y(y-4)<=4�cy=(1,2),3,4
y=3�c
1/4=1/6+1/(3z)+1/(2z)
6z=4z+8+12�cz=10
y=4�c
1/4=1/8+1/(4z)+1/(2z)
2z=z+2+4�cz=6
x=3�c
1/4<=2/(3y)+1/y^2
3y^2-8y<=12
y(3y-8)<=12�cy=3
1/4=1/9+2/(3z)
9z=4z+24�cz=24/5�łȂ�
so�c
(x,y,z)=(1,5,24),(1,6,14),(1,8,9),(2,3,10),(2,4,6)
2(x+y+z)=a+b+c=2s
x=s-a�E�E�Ea=30-1=29, 21-1=20, 18-1=17,
15-2=13, 12-2=10
y=s-b�E�E�Eb=30-5=25, 21-6=15, 18-8=10,
15-3=12, 12-4=8
z=s-c�E�E�Ec=30-24=6, 21-14=7,
18-9=9, 15-10=5, 12-6=6
so�c
(a,b,c)=(29.25,6),
(20,15,7), (17,10,9), (13,12,5), (10,8,6)
��5��ނ�^^
���S�@����}�`�����s�l�ӌ`��Ђ��`�̂Ƃ��A���݂��邩�ǂ����l�@���Ă݂Ă��������B
ab*sin��=2(a+b)
sin��=2(a+b)/(ab)<=1
0<=2(a+b)<=ab
(a-2)(b-2)>=4
�������̂͂�����ł�����܂���^^
���1�Ɏ�����Ă���悤�Ȃ��Ƃł͂Ȃ��A
���͂̒����Ɩʐς����������s�l�ӌ`������Ƃ��A�����悤�ȁ��̑��݂����邩�ǂ����c?
�����̗���F�Ӑ}�͓����}�`�̒��ŁA���͂̒����Ɩʐς��������}�`�����邩�ǂ������l���Ē�����Ƃ������ł���
NO2�u�l�c�����v �@�@04/23 12��32���@��M �X�V 5/12
���P
�@���̒����`�̒��p���͂��ނQ�ӂ̒��������C���i���C���͐������C�������j�Ƃ���ƁC�������C
�@�@�������Q(���{��)
�@�@����(���|�Q)�|�Q(���|�Q)���S
�@�@��(���|�Q)(���|�Q)���S
�@���|�Q�����|�Q���|�P�C���|�Q�C���|�Q�͐����Ȃ̂ŁC
�@�@(���|�Q�C���|�Q)��(�S�C�P)�C(�Q�C�Q)
�@�@��(���C��)��(�U�C�R)�C(�S�C�S)
�@�����͋��ɏ����ɓK����D
���Q
�@���`�a�b�ɂ����āC�`�a���`�b�����C�a�b�����i���C���͐������j�Ƃ���D
�@�O�p�s�������C�a�b���b�`�{�`�a
�@�@���������{��
�@�@���Q�������E�E�E(1)
�@�`����a�b�ɐ����`�g�������ƁC
�@�@�`�g��(�`�a�Q�|�a�g�Q)�P�^�Q��{���Q�|(���^�Q)�Q}�P�^�Q���P�^�Q�E(�S���Q�|���Q)�P�^�Q
�@�ʐςr�́C
�@�@�r���P�^�Q�E�a�b�E�`�g���P�^�S�E��(�S���Q�|���Q)�P�^�Q���Q���{��
�@�w���Q���Ƃ���ƁC
�@�@��(�w�Q�|���Q)�P�^�Q���S(�w�{��)
�@�@�����Q(�w�Q�|���Q)���P�U(�w�{��)�Q
�@�@��(���Q�|�P�U)�w�Q�|�R�Q���w�|���Q(���Q�{�P�U)���O
�@�����O����C
�@�@��(���Q�|�P�U)(�w�^��)�Q�|�R�Q�E�w�^���|(���Q�{�P�U)���O
�@�x���w�^���Ƃ���ƁC
�@�@(���Q�|�P�U)�x�Q�|�R�Q�x�|(���Q�{�P�U)���O
�@�@��(�x�{�P){(���Q�|�P�U)�x�|(���Q�{�P�U)}���O
�@�x���w�^����(�Q��)�^�����O���C
�@�@(���Q�|�P�U)�x�����Q�{�P�U�E�E�E(2)
�@���Q���P�U�Ƃ���ƁC�O���P�U�E�Q�ƂȂ�C��������D
�@�̂ɂ��Q���P�U�ƂȂ�C
�@�@�x��(���Q�{�P�U)�^(���Q�|�P�U)���P�{�R�Q�^(���Q�|�P�U)
�@�x��(�Q��)�^�����C
�@�@�Q���|����(�R�Q��)�^(���Q�|�P�U)�E�E�E(3)
�@�Q���|�����O���C���Q�|�P�U���O
�@�@�������S�E�E�E(4)
�@�Q���|���͐������Ȃ̂ŁC(3)���C
�@�@(�R�Q��)�^(���Q�|�P�U)���P
�@�@���R�Q�������Q�|�P�U
�@�@�����Q�|�R�Q���|�P�U���O
�@�@��(���^�S)�Q�|�W�E���^�S�|�P���O
�@�@���S�|��P�V�����^�S���S�{��P�V
�@�S�|��P�V����P�U�|��P�V���O���C
�@�@�����S(�S�{��P�V)���P�U�{�S��P�V�E�E�E(5)
�@�S��P�V���S��P�U���P�U�C�S��P�V����P�U��P�V����P�V��P�V���P�V���C
�@�@�R�Q���P�U�{�S��P�V���R�R
�@(4)�C(5)����C�T�������R�Q�E�E�E(6)
�@(3)���C�Q���|����(�R�Q��)�^{(���{�S)(���|�S)}���O�E�E�E(3)'
�@������Ƃ���ƁC���{�S�C���|�S����Ȃ̂ŁC(3)'����C
�@�@���^{(���{�S)(���|�S)}
�͐������ł���D��������Ƃ����ƁC
�@�@���^(���Q�|�P�U)����
�@�@�������Q�|���|�P�U�����O
�@���̂��̂Q���������̔��ʎ����c�Ƃ���ƁC���͐����Ȃ̂ŁC
�@�@�c���P�{�U�S���Q
�͕������ł���D
�@�c���P�{�U�S���Q�����Q�i���͐��̐����j�Ƃ���ƁC
�@�@(���{�W��)(���|�W��)���P
�@���{�W���C���|�W���͐����Ȃ̂ŁD
�@�@���{�W�������|�W�����}�P
�@�@�������}�P�C�����O
�@����͂����������ł��邱�Ƃɔ�����D
�@�̂ɂ��͋����ł���D
�@�����Q��'�Ƃ���ƁC(3)'���C
�@�@�Q���|����(�R�Q�E�Q��')�^{(�Q��'�{�S)(�Q��'�|�S)}��(�P�U��')�^{(��'�{�Q)(��'�|�Q)}
�@��'����Ƃ���ƁC���l�ɁC��'�^{(��'�{�Q)(��'�|�Q)}�����i���͐������j�Ƃ��邱�Ƃ��ł���D
�@�@������'�Q�|��'�|�S�����O
�@���̂�'�̂Q���������̔��ʎ����c�Ƃ���ƁC���l�ɁC
�@�@�c���P�{�P�U���Q�����Q�i���͐����j
�Ƃ��邱�Ƃ��ł���D
�@�@��(���{�S��)(���|�S��)���P
�@�@�����{�S�������|�S�����}�P
�@�@�������}�P�C�����O
�@����͂����������ł��邱�Ƃɖ�������D
�@�̂ɂ�'�͋����ł���D
�@��'���Q��''�i��''�͐������j�Ƃ���ƁC
�@�@�����Q��'���S��''
�@�̂ɂ��͂S�̔{���ł���D
�@(6)����C�����W�C�P�Q�C�P�U�C�Q�O�C�Q�S�C�Q�W�C�R�Q
i). �����W�̂Ƃ��C
�@�@�Q���|�W��(�R�Q��)�^{(���{�S)(���|�S)}��(�R�Q�E�W)�^(�P�Q�E�S)���P�U�^�R
�@����͐����ɂȂ�Ȃ��̂ŁC��������D
ii). �����P�Q�̂Ƃ��C
�@�@�Q���|�P�Q��(�R�Q�E�P�Q)�^(�P�U�E�W)���R
�@����́C�����ł���Q(���|�U)����ƂȂ�C��������D
iii). �����P�U�̂Ƃ��C
�@�@�Q���|�P�U��(�R�Q�E�P�U)�^(�Q�O�E�P�Q)���R�Q�^�P�T
�@����͖�������D
iv). �����Q�O�̂Ƃ��C
�@�@�Q���|�Q�O��(�R�Q�E�Q�O)�^(�Q�S�E�P�U)���T�^�R
�@����͖�������D
v). �����Q�S�̂Ƃ��C
�@�@�Q���|�Q�S��(�R�Q�E�Q�S)�^(�Q�W�E�Q�O)���S�W�^�R�T
�@����͖�������D
vi). �����Q�W�̂Ƃ��C
�@�@�Q���|�Q�W��(�R�Q�E�Q�W)�^(�R�Q�E�Q�S)���V�^�U
�@����͖�������D
vii). �����R�Q�̂Ƃ��C
�@�@�Q���|�R�Q��(�R�Q�E�R�Q)�^(�R�U�E�Q�W)���U�S�^�U�R
�@����͖�������D
�@�܂Ƃ߂�ƁC���̂悤�ȓӎO�p�`�`�a�b�͑��݂��Ȃ��D
���R
�@�@���������S(���{���{��)�i���C���C���͐������j
�@�O�������������Ƃ���ƁC
�@�@���������S(���{���{��)���S(���{���{��)���P�Q��
�@�����O����C�������P�Q
�@�O������������C�������������P�Q
�@�@�����Q���P�Q
�@���͐������Ȃ̂ŁC�����P�C�Q�C�R
i). �����P�̂Ƃ��C�������S(�P�{���{��)
�@�@����(���|�S)�|�S(���|�S)���S�{�P�U
�@�@��(���|�S)(���|�S)���Q�O
�@�����P�����������C�|�R�����|�S�����|�S
�@���|�S�C���|�S�͐����Ȃ̂ŁC
�@�@(���|�S�C���|�S)��(�P�C�Q�O)�C(�Q�C�P�O)�C(�S�C�T)
�@�@��(���C��)��(�T�C�Q�S)�C(�U�C�P�S)�C(�W�C�X)
ii). �����Q�̂Ƃ��C�Q�������S(�Q�{���{��)
�@�@���������Q(�Q�{���{��)
�@�@����(���|�Q)�|�Q(���|�Q)���S�{�S
�@�@��(���|�Q)(���|�Q)���W
�@�����Q�����������C�O�����|�Q�����|�Q
�@���|�Q�C���|�Q�͐����Ȃ̂ŁC
�@�@(���|�Q�C���|�Q)��(�P�C�W)�C(�Q�C�S)
�@�@��(���C��)��(�R�C�P�O)�C(�S�C�U)
iii). �����R�̂Ƃ��C�R�������S(�R�{���{��)
�@�@����(�R���|�S)�|�S�^�R�E(�R���|�S)���P�Q�{�P�U�^�R
�@�@��(�R���|�S)(�R���|�S)���T�Q���Q�Q�E�P�R
�@�����R�����������C�T���R���|�S���R���|�S
�@�R���|�S�C�R���|�S�͐����Ȃ̂ŁC���̂悤�Ȃ��C���͑��݂��Ȃ��D
�@�܂Ƃ߂�ƁC
�@�@(���C���C��)��(�P�C�T�C�Q�S)�C(�P�C�U�C�P�S)�C(�P�C�W�C�X)�C(�Q�C�R�C�P�O)�C(�Q�C�S�C�U)
�@���C���C���̑召�W���l���āC
�@�@{���C���C��}��{�P�C�T�C�Q�S}�C{�P�C�U�C�P�S}�C{�P�C�W�C�X}�C{�Q�C�R�C�P�O}�C{�Q�C�S�C�U}�E�E�E(1)
�@�O�p�`�̂R�ӂ̒��������C���C���i���C���C���͐������j�Ƃ���D
�@����(���{���{��)�^�Q�Ƃ���ƁC�ʐςr�́C
�@�@�r��{��(���|��)(���|��)(���|��)}�P�^�Q�����{���{��
�@�@��(���{���{��)�^�Q�E(�|���{���{��)�^�Q�E(���|���{��)�^�Q�E(���{���|��)�^�Q��(���{���{��)�Q
�@���{���{�����O����C
�@�@(�|���{���{��)(���|���{��)(���|���{��)���P�U(���{���{��)�E�E�E(2)
�@�����ŁC
�@�@(�|���{���{��)�{(���|���{��)���Q���C(���|���{��)�{(���{���|��)���Q��
�͋��ɋ����ł���̂ŁC�|���{���{���C���|���{���C���{���|���̋��͈�v����D
�@(1)���C�|���{���{���C���|���{���C���{���|���͋����ł���D
�@�O�p�s�������C�������{���C�������{���C�������{��
�@�̂ɂ��C���C���𐳐����Ƃ��āC
�@�@�|���{���{�����Q���E�E�E(3)
�@�@���|���{�����Q���E�E�E(4)
�@�@���{���|�����Q���E�E�E(5)
�Ƃ���D
�@{(4)�{(5)}���Q���C�������{���E�E�E(6)
�@{(3)�{(5)}���Q���C�������{���E�E�E(7)
�@{(3)�{(4)}���Q���C�������{���E�E�E(8)
�@(2)����C�Q���E�Q���E�Q�����P�U�E{(���{��)�{(���{��)�{(���{��)}
�@�@�����������S(���{���{��)
�@(1)����C
�@�@{���C���C��}��{�P�C�T�C�Q�S}�C{�P�C�U�C�P�S}�C{�P�C�W�C�X}�C{�Q�C�R�C�P�O}�C{�Q�C�S�C�U}
�@(6)�C(7)�C(8)����C
�@�@{���C���C��}��{�U�C�Q�T�C�Q�X}�C{�V�C�P�T�C�Q�O}�C{�X�C�P�O�C�P�V}�C{�T�C�P�Q�C�P�R}�C{�U�C�W�C�P�O}
�i�Q�l�j���p�O�p�`�Ɍ����Čv�Z���Ă݂�D
�@�R�ӂ̒������C
�@�@��(���Q�|���Q)�C�Q�������C��(���Q�{���Q)�i���C���C���͐������C���C���݂͌��ɑf�C�������C���C���͋��Ɋ�ɂȂ邱�Ƃ͂Ȃ��j
�Ƃ���D
�@�ʐςr�́C
�@�@�r���P�^�Q�E��(���Q�|���Q)�E�Q����������(���Q�|���Q)�{�Q�������{��(���Q�{���Q)
�@�@�����Q����(���{��)(���|��)���Q����(���{��)
�@����(���{��)���O����C����(���|��)���Q
�@���C���C���|���͐������Ȃ̂ŁC
i). �����P�̂Ƃ��C��(���|��)���Q
�@�@�������P�C���|�����Q�@�܂��́@�����Q�C���|�����P
�@�@�������R�C�����P�@�܂��́@�����R�C�����Q
�@�������C�����R�C�����Q
�@�̂ɂ��̒��p�O�p�`�̂R�ӂ́C�T�C�P�Q�C�P�R
ii). �����Q�̂Ƃ��C��(���|��)���P
�@�@���������|�����P
�@�@�������Q�C�����P
�@�̂ɂ��̒��p�O�p�`�̂R�ӂ́C�U�C�W�C�P�O
���S
�@�Ђ��`�̏ꍇ�D
�@���ϓI�ɂ́C�ӂ̒������R�C�S�C�T�ł��钼�p�O�p�`���g���āC���̂Ђ��`�������ɍ������Ƃ�������D

�@��ʓI�ɁC�P�ӂ̒��������̂Ђ��`�`�a�b�c�i���͐������j���l����D
�@�Ίp���`�b�C�a�c�̌�_���d�Ƃ���D
�@�ڂ`�a�d���Ɓi�O���Ɓ��^�Q�j�Ƃ���ƁC
�@�@�`�d����sin�ƁC�a�d����cos��
�@�̂ɖʐςr�́C
�@�@�r���P�^�Q�E�`�b�E�a�c���P�^�Q�E�Q��sin�ƁE�Q��cos�Ɓ��Q���Qsin��cos�Ɓ����Qsin�Q�Ɓ��S��
�@�@��sin�Q�Ɓ��S�^��
�@�O��sin�Q�Ɓ��P���C�O���S�^�����P
�@�@�������S
�@�����S�̂Ƃ��C�Ɓ��^�S�ƂȂ�C���P�̐����`�ƂȂ�D
�@�����T�̂Ƃ��C
�@�@�Ɓ��P�^�Q�Earcsin(�S�^��)
�@�̂ɏ��������C�P�ӂ̒��������i���͂T�ȏ�̐����j�̐����`�ȊO�̂Ђ��`�����݂���D

�@���s�l�ӌ`�̏ꍇ�D
�@�����`��Ђ��`�łȂ����s�l�ӌ`�`�a�b�c�ɂ����āC�`�a�����C�`�c�����i���C���͐������C�������j�Ƃ���D
�@�`���璼���a�b�ɐ����`�g�����낵�C�a�g�����i�O���������j�Ƃ���ƁC
�@�@�`�g��(�`�a�Q�|�a�g�Q)�P�^�Q��(���Q�|���Q)�P�^�Q
�@�̂ɖʐςr�́C
�@�@�r���`�c�E�`�g����(���Q�|���Q)�P�^�Q���Q(���{��)
�@�@�����Q(���Q�|���Q)���S(���{��)�Q
�@�@�����Q���Q�����Q���Q�|�S(���{��)�Q
�@�@�����Q��{���Q���Q�|�S(���{��)�Q}�^���Q
�@�@������{���Q���Q�|�S(���{��)�Q}�P�^�Q�^��
�@���̂悤�Ȃ��i�O���������j�����݂���悢�D

�i���W�j���s�l�ӌ`�łȂ����r��`�̏ꍇ���l���Ă݂�D
�@�`�a���b�c�����C�`�c�����C�a�b�����i���C���C���͐������C�������j�ł���C�`�c//�a�b�ł��铙�r��`���l����D
�@�`����a�b�ɐ����`�g�������ƁC
�@�@�`�g��(�`�a�Q�|�a�g�Q)�P�^�Q��[���Q�|{(���|��)�^�Q}�Q]�P�^�Q���P�^�Q�E{�S���Q�|(���|��)�Q}�P�^�Q
�@�ʐςr�́C
�@�@�r���P�^�Q�E(�`�c�{�a�b)�E�`�g���P�^�Q�E(���{��)�E�P�^�Q�E{�S���Q�|(���|��)�Q}�P�^�Q
�@�@�@���Q���{���{��
�@�@��(���{��)�Q{�S���Q�|(���|��)�Q}���P�U(�Q���{���{��)�Q
�@�@���S{(���{��)�Q�|�P�U}���Q�|�U�S(���{��)���|(���Q�|���Q)�Q�|�P�U(���{��)�Q���O
�@���̂��̕��������C���������������Ă悢�D
�@�Ⴆ�C


NO3�u���N���̂�������v 04/27 23��41���@��M �X�V 5/12
���1
�����`�̏c���̒��������ꂼ��x�Ay�Ƃ��܂��B
���̒�����2(x�{y)�A�ʐς�xy �B
(�����̎��́A��{�Ώ̎�����Ȃ��Ă��܂�)
�����̒l���������Ƃ���ƁA
![]()
![]()
���́A�O���t���A3�~6�̒����`�ƁA4�~4�̐����`�ł��B

���2
��ӂ̒�����x�A���̕ӂ̒�����y�̓ӎO�p�`���l���܂��B
���̒����́Ax�{2y�A
�ʐς̓w�����̌������A
![]()
�����̒l���������Ƃ��āA��������ƁA
![]()
�����ŁA���ӂ͋����ł��B
�E�ӂ́Ax�������̂Ƃ������ł����A��̂Ƃ��͊�ł��B
x�͋����łȂ���Ȃ�܂���B
x��2���Ƃ��܂��B
���̒����́A2(m�{y)
�ʐς́A![]()
�����̒l���������Ƃ��āA��������ƁA
![]()
![]()
y�ɂ��ĉ����ƁA
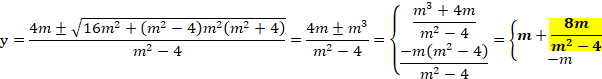
�|m�͕��ɂȂ�̂Ŏ̂Ă܂��B
���F�̕����́A
|
m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
9���� |
|
8m |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
�@��� |
|
m2�|4 |
-3 |
0 |
5 |
12 |
21 |
32 |
45 |
60 |
77 |
�@��� |
|
�l |
�� |
�~ |
4.8000 |
2.6667 |
1.9048 |
1.5000 |
1.2444 |
1.0667 |
0.9351 |
1��菬 |
�\���Ay�����̐����ɂȂ邱�Ƃ͂���܂���B
��xyz��4(x�{y�{z)�������܂��B
���́Ax�Ay�Az�ɂ��đΏ̂ł��B
z��萔�Ƃ��ĂƂ炦�Ax�̕�����y���l���܂��B
![]()
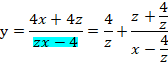
���F�̕������l����ƁA
z��1�̂Ƃ��Ax��1�A2�A3�̂Ƃ�y�͕��Ax��4��y�͒�`����Ȃ��̂ŁA5�ȏ���l���܂��B
z��2�̂Ƃ��Ax��1�̂Ƃ�y�͕��Ax��2��y�͒�`����Ȃ��̂ŁA3�ȏ���l���܂��B
z��3�̂Ƃ��Ax��1�̂Ƃ�y�͕��Ȃ̂ŁA2�ȏ���l���܂��B
z��4�̂Ƃ��Ax��1��y�͒�`����Ȃ��̂ŁA2�ȏ���l���܂��B
���̕������́Ay��x�Ɋւ��đΏ̂ł��B
y�̒l�ׂ�Ƃ��A�͂��߂�x�͏c�̑Q�ߐ��̎��̐����̒l����n�߁A���̂Ƃ���y�̒l���傫��x�͒��ׂ܂���B
y�̒l�������ɂȂ�Ȃ�����ł��B

z��4�̂Ƃ��Ax��1�Ƃ���ƁA
![]()
�Ȃ̂ŁA���̒l���傫��x�ɂ��Ē��ׂ�K�v�͂���܂���B
y�̒l�̕\

�ȏォ��A(1,5,24)�A(1,6,14)�A(1,8,9)�A(2,3,10)�A(2,4,6) �����ł��B
(x�Ay�Az�̏��������ɐ������܂���)
���3
�O�p�`��3�ӂ�x�Ay�Az�Ƃ��܂��B
���̒����́Ax�{y�{z�A
�ʐς̓w�����̌������A
![]()
�����̒l���������Ƃ���ƁA
![]()
![]()
![]()
�����ŁA
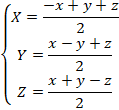
�Ƃ����ƁA
![]()
�Ȃ̂ŁA
![]()
�䂦�ɁA��̌��ʂ�p���āA
 �Ƃ���ƁA
�Ƃ���ƁA![]() �Ȃ̂ŁA
�Ȃ̂ŁA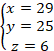
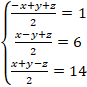 �Ƃ���ƁA
�Ƃ���ƁA![]() �Ȃ̂ŁA
�Ȃ̂ŁA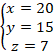
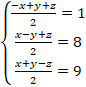 �Ƃ���ƁA
�Ƃ���ƁA![]() �Ȃ̂ŁA
�Ȃ̂ŁA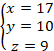
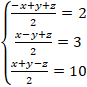 �Ƃ���ƁA
�Ƃ���ƁA![]() �Ȃ̂ŁA
�Ȃ̂ŁA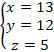
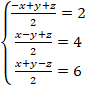 �Ƃ���ƁA
�Ƃ���ƁA![]() �Ȃ̂ŁA
�Ȃ̂ŁA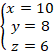
�܂�A3�ӂ��A(29,25,6)�A(20,15,7)�A(17,10,9,)�A(13,12,5)�A(10,8,6) �̎O�p�`�ł��B
�g���̉��́A���p�O�p�`�ł��B
���4
�����߂ɂЂ��`���l���܂��B
�Ђ��`��1�ӂ̒�����x�A���p��1�̑傫�����ƂƂ��܂��B
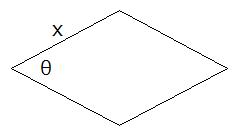
���̒�����4x�A�ʐς�x2sin�Ƃł��B
�����̒l���������Ƃ���ƁA
![]()
![]()
x��4,5,6,��� �̂Ƃ��A�������܂��B
x��4�̂Ƃ��́A���1�̐����`�̂Ƃ��ł��B
�����ɕ��s�l�ӌ`���l���܂��B
�u�l�ӌ`��2�ӂ̒�����x�Ay�A���p�̈�̑傫�����ƂƂ��܂��B
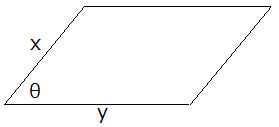
���̒�����2(x�{y)�A�ʐς�xy sin�Ƃł��B
�����̒l���������Ƃ���ƁA
![]()
![]()
![]()
![]()

�O���t���A
x��1,2�̂Ƃ��́A�������܂���B
x��3�̂Ƃ��́Ay��6�ȏ�̐����ł��B
x��4�̂Ƃ��́Ay��4�ȏ�̐����ł��B
x��5�̂Ƃ����Ay��4�ȏ�̐����ł��B
x��6�̂Ƃ��́Ay��3�ȏ�̐����ł��B
x��7�ȏ�̂Ƃ��́Ay��3�ȏ�̐����ł��B
NO4�u�O�p��K�v
05/08 22��54���@��M �X�V 5/12
10�A�x���C���x���`�������W�����̂ł����B
����̓L�`���Ɖ������Ƃ��ł��܂���ł����B
�y���P�z
���s����̌�G�N�Z���܂œ������ĒT���C�Y�t�}�̂Q�������͂��܂������C�u�������v�Ƃ�������̂ł͂���܂���B
�����̗���F��蕶�̕s���ɂ��A���l�тƂ��܂���
���P�@����}�`�������`�i�����`���܂ށj�ł���Ƃ��A����������Ȃ����B
�@�@�@�@�i�Q����܂��j
���̌��ł����A�����`�i�����`���܂ށj�̒��ōl���āA
�@�ӂ̒��������ׂĐ����ŁA���̒����Ɩʐς������Ƃ����Ӗ��ŏo�肵�܂����B
�ŁA���̎O�p�`�Ƃ̑g�łȂ��āA�����}�`�̒��ł̈Ӑ}�ł����B
�@�ŁA�@�i�Q����܂��j�Ƃ����\�������Ă��܂��āA2�g�Ƃ͕\�����Ă���܂���B
������ɂ��Ă��A����ӂ��������ƂɂȂ�A���l�т��܂��B
�@������A�������ꂽ�O�p�`�ƒ����`��2�g�ł����A
���̎��̕�����ςȉ��l������܂��B
�@�N�����ׂĂ��Ȃ���A�����������ł��B
�A�b�v�����Ƃ��A�����������ꂽ���͋������̂ł͂Ȃ��ł��傤���B
�@
�y���R�z
�s�������
�@xyz��4(x�{y�{z)
�́C
�@(x, y, z)��(1,5,24), (1,6,14), (1,8,9), (2,3,10), (2,4,6)
�Ɖ������Ƃ��ł��C����炩��
�@(x�{y, x�{z, y�{x)��(6,25,29), (7,15,20), (9,10,17),
(5,12,13), (6,8,10)
�����ƁC�����3����3�p�`��3�ӂ��Ȃ��C�ʐςƎ��������������l�ɂȂ�Ƃ���܂ł͂킩�����̂ł����C���̉Ɍ��т��邱�Ƃ��ł��܂���B
����͂���A�̕��X�̉���������Ă��������܂��B
�ł́C�܂�����i��������ł����j�B
�����̗��ꂩ��A��ŋC���t�����̂ł����A���R����288��w�����̎O�p�`�i�Q�j�Ɠ������ł����B�����o�肵�Ă���Ɠ����v�l�Ɋׂ肨�������������B��
NO3�u���N���̂�������v 05/19 16��48���@��M �X�V 5/19
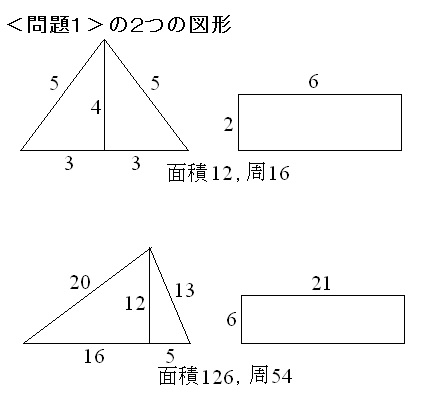
��372��m�����Ɩʐς������}�`�n�̖��ŁA�u�O�p��K�v����̖��1���܂˂Ă݂܂����B
����1�������̂ŁA�����Ă݂܂��B
����ɉ������邩�́A������܂���B
���̍l�����A����m�An�̊���U�����Ɏ�����Ă��Ȃ���ł��B
�l���̂��炷���������܂��B
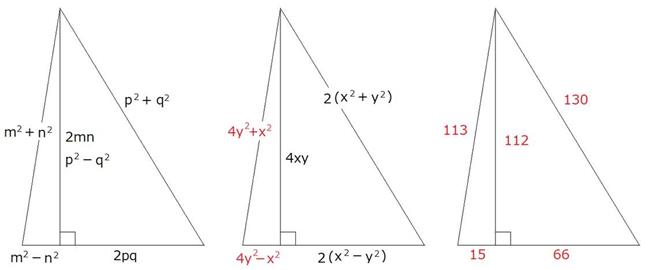
���̐}�̂悤�ɁA���p�O�p�`��2�Ȃ��܂��B
2mn��p2−q2��(p�{q)(p�\q)
m�An�Ap�Aq�͐����ł��B
���ӂ������ł��邱�Ƃ���Ap�Aq�̘a���Ƃ��ɋ����ł��B
p�{q��2x
p�\q��2y
�Ƃ����܂��B
2mn��(p�{q)(p�\q)��4xy
mn��2xy
�����ŁAm�An�̊���U��͎��̂悤�ł��B(m��n�Ax��y)
|
�@ |
�@ |
�A |
�B |
�C |
�D |
�E |
|
m |
2xy |
2x |
2y |
xy |
x |
���̑� |
|
n |
1 |
y |
�� |
2 |
2�� |
�B�̏ꍇ
���́A(4y2+x2)�{2(x2+y2)�{(4y2-x2)�{2(x2-y2)��2(2x2+4y2)
�ʐς́A{(4y2-x2)�{2(x2-y2)}�~2xy��2xy(x2+2y2)
�����`��1�ӂ�A�Ƃ���ƁA
(2x2+4y2−A)A��2xy(x2+2y2)
�����A��2���������Ƃ��ĉ����A�����̒����������ɂȂ�悤�ɂ��܂��B
����ƁA�ʓ|�Ȍv�Z�����āA���̒����`��������܂��B

NO3�u���N���̂�������v 06/04 21��33���@��M �X�V 6/05
��372��m�����Ɩʐς������}�`�n�̖��ŁA����2�������̂ŁA�����܂��B
����ɉ������邩�́A������܂���B
�l�����͑O��Ɠ����ł��B
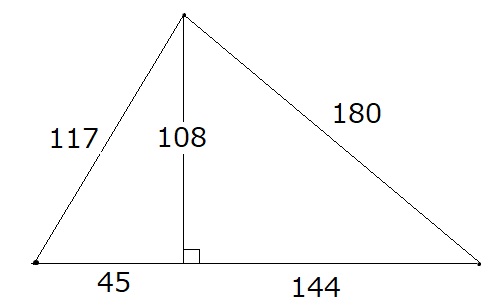
�����`�́A54�~189�ł��B
2���@�O�p�`�́A
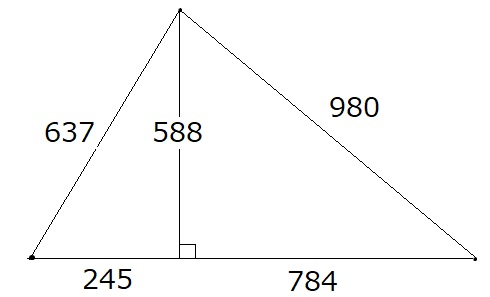
�����`�́A294�~1029�ł��B
NO3�u���N���̂�������v 06/05 18��56���@��M �X�V 6/06
�O�p�`�ƒ����`�Ŏ��̒����Ɩʐς����������̂���ׂ܂��B
�i���łɘA���������̂ƐV�������̂�����܂��B�܂��A�A�ƇD�͑����ł��B�j

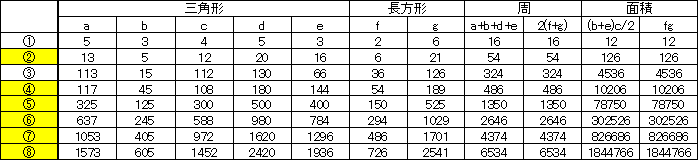
��̌��ʂ����܂��B�i�@�ƇB�͏Ȃ��܂��j
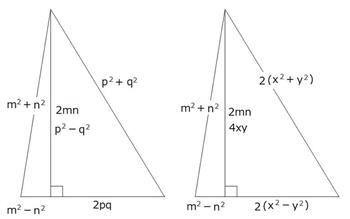
��̍��̐}�ŁA2mn=p2�|q2��(p�{q)(p�|q) �ł��B
p�{q��2x�Ap�|q��2y �Ƃ����ƁA
p��x�{y�Aq��x�|y �Ȃ̂ŁA�E�̐}�̂悤�ɍl���܂��B

k�͊�ł��B
��̕\��k�ŕ\���Ă݂܂��B
m��3k�An��2k�Am2�{n2��13k2�Am2�|n2��5k2�A2mn��12k2�A
xy��3k2�Ax��3k�Ay��k�A2(x2�{y2)��20k2�A2(x2�|y2)��16k2�A
f��6k2�Ag��21k2�A�ł��B
�O�p�`�̎��́Aa�{b�{d�{e��13k2�{5k2�{20k2�{16k2��54k2
�����`�̎��́A2(f�{g)��2(6k2�{21k2)
�O�p�`�̖ʐς́A(b�{e)c/2��(5k2�{16k2)�~12k2�^2
�����`�̖ʐς́Afg��6k2�~21k2
�ƂȂ�܂��B
�@ �A�B�̃p�^�[���ɂ��ẮA�킩��܂���B
NO3�u���N���̂�������v 06/06 09��53���@��M �X�V 6/06
�ӂƋC�Â����̂ő���܂��B
����̐����́A���ׂđ����ł����B
�A�A�C�A�D�A�E�A�F�A�G�͓������̂ł����B
�B�̂��Ƃ��l���Ă��ċC�t���܂����B
���LJA�ƇB�ȊO�́A���̂Ƃ��땪����܂���B
���Ⴂ���炵�܂����B
NO3�u���N���̂�������v 06/09 17��41���@��M �X�V 6/10
�O��́A���Ⴂ�Ő\����܂���ł����B
����́A���Ȃ��Ǝv���܂��B
�����������ׂĒ萫�I�Ȃ��Ƃ����肻���ȋC�����܂�������͎~�߂܂��B
���̎O�p�`�����܂�A�E�̎O�p�`���v�Z�ŋ��߂���悤�Ɋ����܂��B
�܂��A�����`���O�p�`�̒�ӈȊO�̂��̂ɂ��ẮA���͗ǂ��킩��܂���B
�y�P�z�s�^�S���X��

���p�O�p�`��3�ӂɂ����鐔�́A��̕\�̒��ɂ�����܂��B
�������A�@�ƇA�͑����̒��p�O�p�`�ł��B
�A�̕�a��b�����ւ���ƁA6�A8�A10�ƂȂ�킩��₷���Ȃ�܂��B
�������A�Ⴆ�A�O�ӂ�9�A12�A15�̂��̂́A�\�ɂ͌���܂���B
15��1�{14��2�{13��3�{12��4�{11��5�{10��6�{9��7�{8 �̂悤��2�Ƃ��������ɂ͂Ȃ�Ȃ�����ł��B
�y�Q�z�O�p�`�ƒ����`�̎��Ɩʐς��������Ƃ����ꍇ���l���܂��B
�悸�A���ʂ�\�ɂ��Đ������܂��B

�����`�̏c�́A��b�̔����A����a��d�̘a�Ƃ��܂��B
����Ɩʐς͕K���������̂ŁA���̒����ׂ�悢���ƂɂȂ�܂��B
�y�R�z���āA���̍��̐}��AB�̔����̒�����AD�Ƃ��AOB��OC�{CD�̏ꍇ���l���܂��B
�_B�̍��W��(x,y)�Ƃ��܂��B
![]()
![]()
��r���Đ�������ƁA![]() �ƂȂ�܂��B
�ƂȂ�܂��B
����OB�ɓ_������Ă����(on)�AOB��OC+CD�ł��B
OB�̏���ɓ_�������(over)�AOB��OC�{CD�ł��B
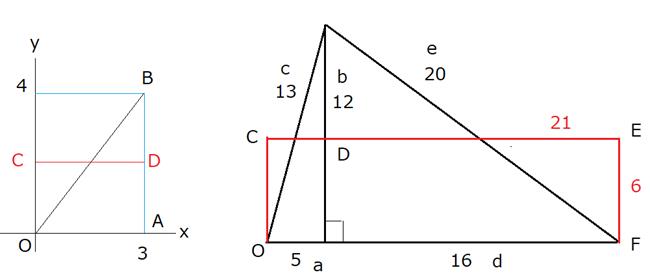
��̉E�̐}�ŁA
c��13�AOC�{CD��6�{5��11���Ac�̕���2�����ł��B
e��20�ADE�{EF��16�{6��22���ADE�{EF�̕���2�����ł��B
���ׂ�Ƃ��A�O�p�`�̒�ӂƒ����`�̉��̕ӂƂ͓������̂ŁA
(c�{e)��(OC�{CD�{DE�{EF)�ł݂܂��B
������c���Ac�|(b/2�{a)�����A
�E����DE�{EF���Ad�{b/2�|e�����̂ŁA
c�|(b/2�{a)��d�{b/2�|e���A
e�|d��a�{b�|c
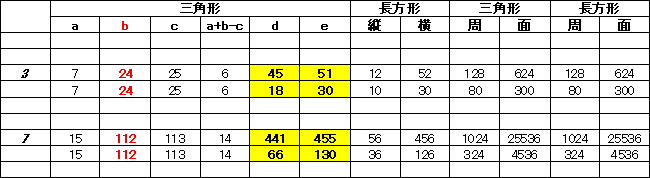
���̌��ʂ�p���ĉ���T���ɂ́A
���̕\��p�ӂ��܂��B
�s�^�S���X���̕\��b�̒����Ń\�[�g���A�ΕӂƉ��̕ӂ̍����L�����Ă����܂��B
5(a)�A12(b)�A13(c)�̑��_��T���ɂ́A�悸a�{b�|c��5�{12�|13��4���v�Z���܂��B
�\��b��12�̂Ƃ��������ƁA����8�A2��2��������܂���B�i4�̂��̂͂���܂���j
���ɁA12(b)�̖�4��6�܂ŕ\����ɂ����܂��B
d�Ab�Ae�́A8�A6�A10�i����2�j�Ȃ̂ŁA2�{����ƁA16�A12�A20�i����4�j�ł��B
�ΕӂƉ��̕ӂ̍���4�Ȃ̂ł�����̗p���܂��B
�O�̂��߁A12(b)�̖�4�܂ŕ\����ɂ����܂��B
d�Ab�Ae�́A3�A4�A5�i����2�j�Ȃ̂ŁA3�{����ƁA9�A12�A15�i����6�j�ł��B
�ΕӂƉ��̕ӂ̍���6�Ȃ̂ł���͂��߂ł��B
����ȗv�̂ʼn������܂�܂��B

�܂��A�y�Q�z�̉���3��7�ɂ͕ʉ��������Ď��̂��̏��������܂��B
NO3�u���N���̂�������v 06/10 18��36���@��M �X�V 6/10
372�lj�3
�O�p�`�ƒ����`�̎��Ɩʐς��������Ƃ����ꍇ����ʓI�ɍl���܂��B
�����`�̏c�́A��b�̔����A����a��d�̘a�Ƃ��܂��B
����Ɩʐς͕K���������̂ŁA���̒����ׂ�悢���ƂɂȂ�܂��B

�O�p�`��2�ӂƒ����`��3�ӂ̘a���������Ȃ�悢�킯�ł��B
OP�{PQ��OC�{CD�{DE�{EQ
a�Ab�Ad��p���Đ������܂��B
![]()
d�Ő������܂��B
![]()
![]()
![]()
![]()
![]()
���̎���d��2���������Ƃ��ĉ����ƁA
![]()
���߂ɁAOP�̌X����4/3�ȏ�Ƃ��Ă����ƁA�����́{���K���Ȃ̂ŁA
![]()
�Ⴆ�Aa=3�Ab��4�Ƃ���ƁA
![]()
�Ⴆ�Aa=5�Ab��12�Ƃ���ƁA
![]()
�ƂȂ�A���̕\�ƈ�v���܂��B

���R�����g�F����̖�A�ӂƕ����̂ŏ����܂����B372�͂���Ŏ~�߂܂��B��
NO3�u���N���̂�������v 06/12 16��48���@��M �X�V 6/12
���R�����g�F����z�[���y�[�W�̎��̈����6/10�̂Ƃ�����������Ƃ��ɁA���ɓI�ȍl���Ƃ������̂ł܂������܂��B
���܂���3�́A���̒��p�O�p�`�����܂�A�E�̒��p�O�p�`�����܂�܂��B
�������A��ӂ̘a�������`�̉��ɂȂ�Ƃ������̂ł����B
�ʉ��S�͏o���܂���B
���܂���4�̕��́A���܂���3�ŕʉ��Ƃ������̂��T���܂��B
���̕������ɓI�ȍl���ɂ��߂��Ǝv���܂��B
��������Ԃ͂�����܂��B��
372�lj�4
�y�悸�z�O�p�`�ƒ����`�̎��Ɩʐς��������Ƃ����ꍇ����ʓI�ɍl���܂��B
�����`�̏c�́A��b�̔����Ɍ��炸f�A����g�Ƃ��܂��B
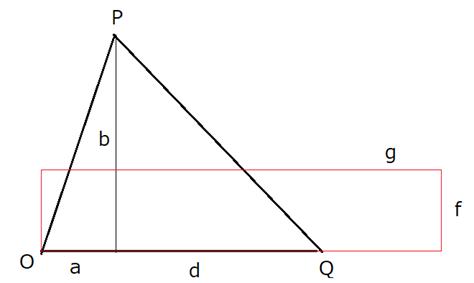
�����̒��p�O�p�`�����Ƃɍl���܂��B
��a�A�cb�̒��p�O�p�`�̎Εӂ͐����ł��B(given)
�����ɉ�d�̒��p�O�p�`�������Ƃ��ɁA�Εӂ������ƂȂ�A���̒����Ɩʐς����������`�����邩�l���܂��B
�E�̒��p�O�p�`�̎Εӂ̒����́A![]() �ł��B
�ł��B
���ꂪ�����łȂ���Ȃ�܂���B
![]() �Ƃ����܂��B
�Ƃ����܂��B
![]()
b�������Ƃ��܂��B�i�����k�{d�Ak�|d���Ƃ��Ɋ�ŁAk�Ad�������ɂȂ�Ȃ��j
k�Ad�͂Ƃ��Ɋ���A�Ƃ��ɋ����ł��B
�y��̗�P�za��7�Ab��24�̂Ƃ��ׂ܂��B
![]()
576��f������������ƁA576��26�~32
24�܂ł̋����̖����������ɕ��ׂ�ƁA2�A4�A6�A8�A12�A16�A18�A(24)

�\����A����3�ӂ������p�O�p�`���Ȃ���悢�킯�ł��B(45�A24�A51)�A(18�A24�A30)
�y��̗�Q�za��15�Ab��112�̂Ƃ��ׂ܂��B
![]()
12544��f������������ƁA576��28�~72
112�܂ł̋����̖����������ɕ��ׂ�ƁA2�A4�A8�A14�A16�A28�A32�A56�A64�A98�A(112)
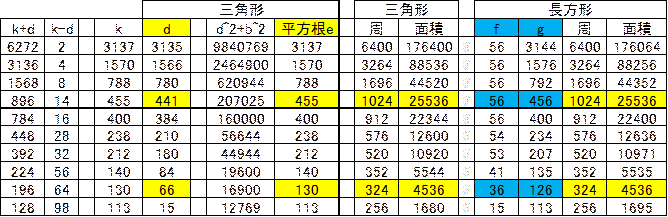
�\����A����3�ӂ������p�O�p�`���Ȃ���悢�킯�ł��B(441�A112�A455)�A(66�A112�A130)
�y�������z
�O�p�`�̎��̒����́A
![]()
�O�p�`�̖ʐς́A
![]()
�����`�̏c�Ɖ���f�Ag�Ƃ���A
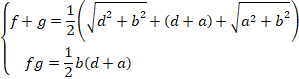
f�Ag�������Ȃ̂Řa�������łȂ���Ȃ�܂���B
�a��w�Ƃ����܂��B
![]()
��������ƁA
![]()
![]()
![]()
![]()
w�ɂ��ĉ����ƁA

�����̒�������ƁA

![]()
![]()
![]()
���ꂪ�������łȂ���w�������ɂȂ�܂���B�i�ʓ|�Ȍv�Z�����邱�Ƃ��Ȃ����R�ł����j
![]()
�Ƃ����܂��B
![]()
�ƂȂ��ɖ߂�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@