2019年令和元年５月１２日

[流れ星]

　　　　第373回数学的な応募問題

　　　　＜解答募集期間：5月12日〜６月9日＞

［大垣八幡宮奉納算術］

　先日、友人から、大垣八幡神社に奉納された算額を頂き、解いてみてはどうですかとメールをもらった問題を参考にして、改題して出題します。

ここでは、半径がｒの円ＯをＯ（ｒ）で表すことにします。

補題

それでは実際の奉納問題です。

問題　

問題を現代風に書き変えます。

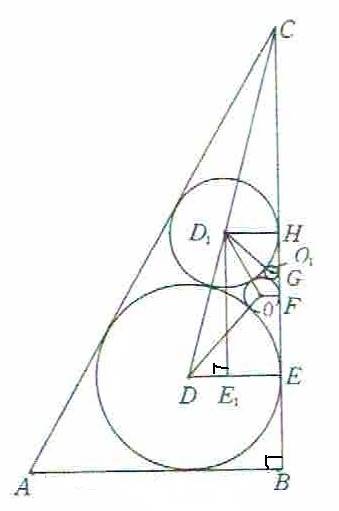
直角三角形ＡＢＣの中へ図にある辺に接する４個の円元Ｄ（a）、享Ｄ_１（ｂ）、貞Ｏ（ｃ）、利Ｏ_１（ｄ）を図のように外接すように入れる。貞の直径２ｃは4寸、利の直径２ｄは1寸4分4厘のとき、直角を挟む長い方の辺の長さは１４４寸であることを示せ。ただし、中心がＤで半径ｒの円をＤ(ｒ)で表す。また、点Ｅ，Ｆ，Ｇ，Ｈはそれぞれの円の辺BC上の接点とする。また、点Ｅ_１はＤ_１から線分ＤＥに下ろした垂線の足とする。

ここで、発展問題です。

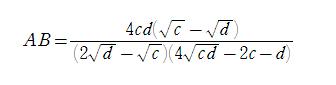
となることを示せ。

＜水の流れ＞初め、股がどこの長さか理解できずにいて、悩みましたので、参考に書いておきます。

釣股弦の術　江戸時代の数学「和算」では直角三角形を釣股弦，三平方の定理のことを釣股弦の術という。　底辺を股，高さを釣（鈎，勺などとも書く），斜辺を弦と呼び，股＞釣と約束する。直角三角形がどのような向きにあっても，直角を挟む長い方の辺を股，短い方の辺を釣と言います。

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。