2019年令和元年６月９日

[流れ星]

　　　　第373回数学的な応募解答

　　　　＜解答募集期間：5月12日〜６月9日＞

［大垣八幡宮奉納算術］

　先日、友人から、大垣八幡神社に奉納された算額を頂き、解いてみてはどうですかとメールをもらった問題を参考にして、改題して出題します。

ここでは、半径がｒの円ＯをＯ（ｒ）で表すことにします。

補題

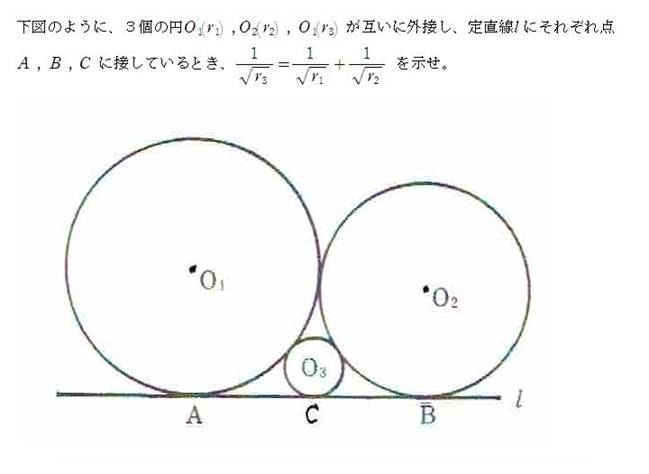
それでは実際の奉納問題です。

問題　

問題を現代風に書き変えます。

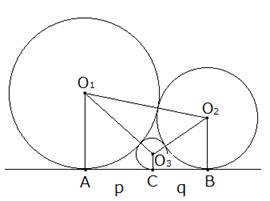
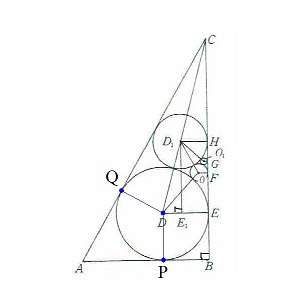
直角三角形ＡＢＣの中へ図にある辺に接する４個の円元Ｄ（a）、享Ｄ_１（ｂ）、貞Ｏ（ｃ）、利Ｏ_１（ｄ）を図のように外接すように入れる。貞の直径２ｃは4寸、利の直径２ｄは1寸4分4厘のとき、直角を挟む長い方の辺の長さは１４４寸であることを示せ。ただし、中心がＤで半径ｒの円をＤ(ｒ)で表す。また、点Ｅ，Ｆ，Ｇ，Ｈはそれぞれの円の辺BC上の接点とする。また、点Ｅ_１はＤ_１から線分ＤＥに下ろした垂線の足とする。

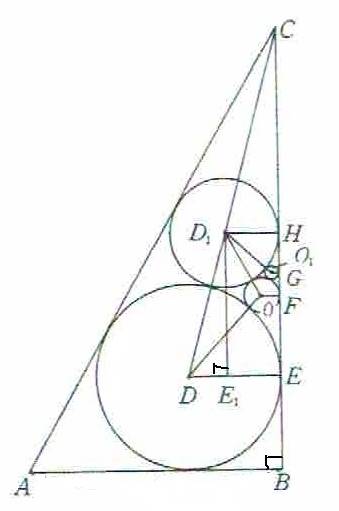
ここで、発展問題です。

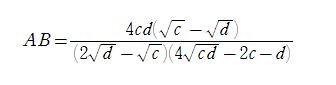
となることを示せ。

＜水の流れ＞初め、股がどこの長さか理解できずにいて、悩みましたので、参考に書いておきます。

釣股弦の術　江戸時代の数学「和算」では直角三角形を釣股弦，三平方の定理のことを釣股弦の術という。　底辺を股，高さを釣（鈎，勺などとも書く），斜辺を弦と呼び，股＞釣と約束する。直角三角形がどのような向きにあっても，直角を挟む長い方の辺を股，短い方の辺を釣と言います。

NO1「早起きのおじさん」 05/16 20時15分　受信 更新 6/9

373解答　早起きのおじさん

補題

AC＝p、BC＝qとします。

円O₁とO₃をみて、

円O₂とO₃をみて、

円O₁とO₂をみて、

(1)より、(2)より、これを(3)に代入すると、

問題

a、bの長さを求めます。

円O、D₁、O₁をみて、

円D、D₁、Oをみて、

別に、

ここで、c＝2、d＝0.72を代入すると、

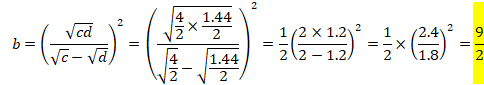
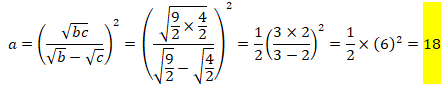
先ず、BCの長さを求めてみます。

BC＝BE＋ECです。

△D₁E₁Dが直角三角形なので、

△D₁E₁D∽△CEDなので、

よって、

次にABの長さを求めてみます。

△ABCが直角三角形なので、

です。

AL＝AM＝x とおきます。

AC＝AL＋LC＝x＋EC＝x＋24

AB＝AM＋MB＝x＋a=x＋18

BC＝42

よって、

よって、AB＝126＋18＝144

これらの結果を比べて長い方の辺の長さは144寸。

発展問題

MB＝a

として、計算してみると、

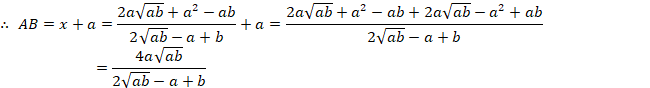
おまけ

直角二等辺三角形になる場合を調べます。

として考えます。

上の結果から、

これらが等しいとすると、

両辺をabで割ります。

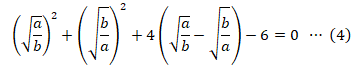
ここで、 とおきます。

よって、式(4)は、

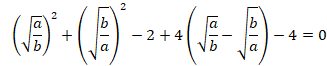
この2次方定式を解くと、(t＞0)

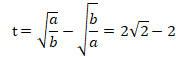
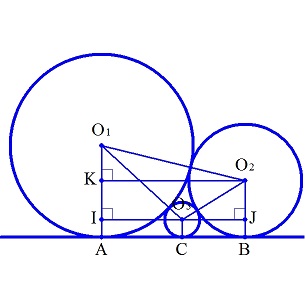
この二つの円に外接する三角形は上のような概形になります。

NO2「浜田明巳」 05/20 13時44分　受信 更新 6/9

補題
　Ｏ_３を通り，ＡＢに平行な直線と，Ｏ_１Ａ，Ｏ_２Ｂとの交点をそれぞれＩ，Ｊとすると，
　　ＡＣ＝ＩＯ_３＝(Ｏ_１Ｏ_３^２−Ｏ_１Ｉ^２)^１／２
　　　　＝{(ｒ_１＋ｒ_３)^２−(ｒ_１−ｒ_３)^２}^１／２
　　　　＝２(ｒ_１ｒ_３)^１／２
　同様に，
　　ＢＣ＝Ｏ_３Ｊ＝２(ｒ_２ｒ_３)^１／２
　ｒ_１＞ｒ_２として、Ｏ_２からＯ_１Ａに垂線Ｏ_２Ｋを下ろすと，同様に，
　　ＡＢ＝ＫＯ_２＝２(ｒ_１ｒ_２)^１／２
　ＡＢ＝ＡＣ＋ＢＣより，２(ｒ_１ｒ_２)^１／２＝２(ｒ_１ｒ_３)^１／２＋２(ｒ_２ｒ_３)^１／２
　ｒ_１ｒ_２ｒ_３≠０より，１／√ｒ_３＝１／√ｒ_１＋１／√ｒ_２


問題
　２ｃ＝４，２ｄ＝１.４４より，ｃ＝２，ｄ＝１.４４／２
　円Ｄ，Ｄ_１，Ｏにおいて，補題より，
　　１／√ｃ＝１／√ａ＋１／√ｂ
　円Ｏ，Ｄ_１，Ｏ_１において，補題より，
　　１／√ｄ＝１／√ｃ＋１／√ｂ＝(１／√ａ＋１／√ｂ)＋１／√ｂ＝１／√ａ＋２／√ｂ
　ｐ＝１／√ａ，ｑ＝１／√ｂとすると，
　　ｐ＋ｑ＝１／√ｃ＝１／√２＝√２／２・・・(1)
　　ｐ＋２ｑ＝１／√ｄ＝√２／√１.４４＝√２／１.２＝５√２／６・・・(2)
　(2)−(1)より，ｑ＝√２／３
　(1)より，ｐ＝√２／２−√２／３＝√２／６
　　∴１／√ａ＝√２／６，１／√ｂ＝√２／３
　　∴ａ＝１８，ｂ＝９／２

　補題より，
　　ＥＦ＝２(ａｃ)^１／２＝２(１８・２)^１／２＝１２
　　ＦＨ＝２(ｂｃ)^１／２＝２(９／２・２)^１／２＝６
　　∴ＥＨ＝ＥＦ＋ＦＨ＝１２＋６＝１８
　△ＣＤＥにおいて，Ｄ_１Ｈ：ＤＥ＝ｂ：ａ＝(９／２)：１８＝１：４
　　∴ＥＣ＝４／３・ＥＨ＝４／３・１８＝２４
　円ＤとＡＢ，ＡＣとの接点をそれぞれＰ，Ｑとすると，
　　ＢＥ＝ＢＰ＝ａ＝１８
　　ＥＣ＝ＣＱ＝２４
　さらに，
　　ＡＰ＝ＡＱ＝ｘ
とする．
　△ＡＢＣにおいて，ＡＢ^２＋ＢＣ^２＝ＡＣ^２
　　∴(ｘ＋１８)^２＋(１８＋２４)^２＝(ｘ＋２４)^２
　　∴２・１８・ｘ＋１８^２・２＋２・１８・２４＝２・２４・ｘ
　　∴２・６・ｘ＝２・１８・(１８＋２４)
　　∴ｘ＝１２６
　　∴ＡＢ＝ｘ＋１８＝１４４


発展問題
（最初，{４ｃｄ(√ｃ−√ｄ)}／[(２√ｄ−√ｃ)[{４(ｃｄ)^１／２−２ｃ−ｄ}]に，ｃ＝２，ｄ＝１.４４／２
を代入するだけか，と思ってしまいました．忖度します）
　上記問題より，
　　１／√ａ＋１／√ｂ＝１／√ｃ・・・(1)
　　１／√ａ＋２／√ｂ＝１／√ｄ・・・(2)
　(2)−(1)より，１／√ｂ＝１／√ｄ−１／√ｃ
　(1)より，１／√ａ＝１／√ｃ−(１／√ｄ−１／√ｃ)＝２／√ｃ−１／√ｄ
　ａ，ｂは存在するので，
　　√ａ＝(√ｃ√ｄ)／(２√ｄ−√ｃ)，√ｂ＝(√ｃ√ｄ)／(√ｃ−√ｄ)・・・(3)
　このとき，ＥＨ＝２√ａ√ｂ
　ＤＥ：Ｄ_１Ｈ＝ａ：ｂから，
　　ＥＣ＝ａ／(ａ−ｂ)・ＥＨ＝(２ａ√ａ√ｂ)／(ａ−ｂ)
　　∴ＢＣ＝ＢＥ＋ＥＣ＝ａ＋(２ａ√ａ√ｂ)／(ａ−ｂ)
　ＡＰ＝ＡＱ＝ｘとすると，
　　ＡＢ＝ＡＰ＋ＰＢ＝ｘ＋ａ
　　ＡＣ＝ＡＱ＋ＱＣ＝ｘ＋(２ａ√ａ√ｂ)／(ａ−ｂ)
　ＡＢ^２＋ＢＣ^２＝ＡＣ^２より，
　　(ｘ＋ａ)^２＋{ａ＋(２ａ√ａ√ｂ)／(ａ−ｂ)}^２＝{ｘ＋(２ａ√ａ√ｂ)／(ａ−ｂ)}^２
　　∴２ａｘ＋２ａ^２＋２ａ・(２ａ√ａ√ｂ)／(ａ−ｂ)＝２ｘ・(２ａ√ａ√ｂ)／(ａ−ｂ)
　　∴２ａ{(２√ａ√ｂ)／(ａ−ｂ)−１}ｘ＝２ａ^２{１＋(２√ａ√ｂ)／(ａ−ｂ)}
　ａ≠０より，
　　{２√ａ√ｂ−(ａ−ｂ)}ｘ＝ａ{(ａ−ｂ)＋２√ａ√ｂ}
　ｘは存在するので，
　　ｘ＝ａ・{(ａ−ｂ)＋２√ａ√ｂ}／{２√ａ√ｂ−(ａ−ｂ)}
　　∴ＡＢ＝ｘ＋ａ＝ａ・{(ａ−ｂ)＋２√ａ√ｂ}／{２√ａ√ｂ−(ａ−ｂ)}＋ａ
　　　　　＝ａ・[{(ａ−ｂ)＋２√ａ√ｂ}＋{２√ａ√ｂ−(ａ−ｂ)}]／{２√ａ√ｂ−(ａ−ｂ)}
　　　　　＝(４ａ√ａ√ｂ)／{２√ａ√ｂ−(ａ−ｂ)}
　(3)より，
　　ＡＢ＝４・[(ｃｄ)／(２√ｄ−√ｃ)^２・(ｃｄ)／{(２√ｄ−√ｃ)(√ｃ−√ｄ)}]
　　　　　　　／[(２ｃｄ)／{(２√ｄ−√ｃ)(√ｃ−√ｄ)}−(ｃｄ)／(２√ｄ−√ｃ)^２＋(ｃｄ)／(√ｃ−√ｄ)^２]
　ｃｄ≠０より，
　　ＡＢ＝{４ｃｄ・(√ｃ−√ｄ)／(２√ｄ−√ｃ)}／{２(２√ｄ−√ｃ)(√ｃ−√ｄ)−(√ｃ−√ｄ)^２＋(２√ｄ−√ｃ)^２}
　　　　＝{４ｃｄ(√ｃ−√ｄ)}
　　　　　　　／[(２√ｄ−√ｃ){２(−ｃ−２ｄ＋３√ｃ√ｄ)−(ｃ＋ｄ−２√ｃ√ｄ)＋(４ｄ＋ｃ−４√ｃ√ｄ)}]
　　　　＝{４ｃｄ(√ｃ−√ｄ)}／{(２√ｄ−√ｃ)(４√ｃ√ｄ−２ｃ−ｄ)}

NO3「三角定規」 06/03 10時25分　受信 更新 6/9