椷榓尦擭俇寧俋擔
 [棳傟惎]
[棳傟惎]
丂丂丂丂戞374夞悢妛揑側墳曞栤戣
丂丂丂丂亙夝摎曞廤婜娫丗6寧9擔乣7寧7擔亜
乵奅幬丒戝幬偺挿偝乶
丂姲惌3擭乮1791乯偺戝奯巗偺戝奯敧敠媨偵14戣偺嶼妟偑曭擺偝傟偰偄傑偡丅偦偺偆偪偺戞榋栤戣偑戞俇恾偱偡丅

丂傑偨丄壝塱俁擭乮1850乯偵偼婒晫導孲忋巗偺孲忋敧敠恄幮偵係戣偺嶼妟偑曭擺偝偊偰偄傑偡丅偦偺偆偪偺戞堦栤戣偑戞1恾偱偡丅

拲丗恾偱偼捈妏嶰妏宍偵尒偊傑偡偑丄幚嵺偼偨偩偺嶰妏宍偵側傝傑偡丅
丂偦偙偱丄忋偺2戣傪嶲峫偵偟偰丄夵戣偟偰弌戣偟傑偡丅
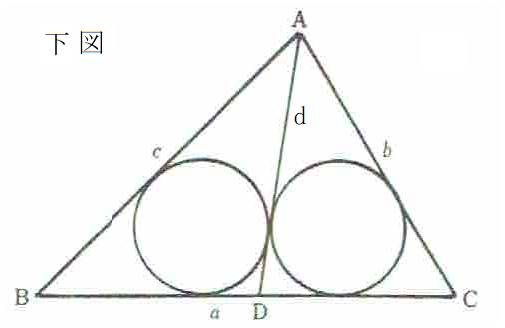
栤戣侾丂壓恾偵偍偄偰丄佢俛偑捈妏側捈妏嶰妏宍俙俛俠偺曈俛俠偵擇偮偺嶰妏宍俙俛俢偲俙俠俢偺撪愙墌偺敿宎偑摍偟偄傛偆偵揰俢傪偲傞丅
偙偺偲偒丄慄暘俙俢亖倓偺挿偝偼丂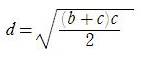 偱偁傞偙偲傪帵偣丅
偱偁傞偙偲傪帵偣丅
丂拲丗戝奯敧敠媨偺栤戣偼俛俠亖a亖侾俆丄俙俠亖倐亖侾俈丄俙俛亖們亖俉偺偲偒丄俙俢亖倓亖侾侽傪帵偡丅
栤戣俀丄摨偠壓恾偵偍偄偰丄嶰妏宍俙俛俠偺曈俛俠偵擇偮偺嶰妏宍俙俛俢偲俙俠俢偺撪愙墌偺敿宎偑摍偟偄傛偆偵揰俢傪偲傞丅
偙偺偲偒丄慄暘俛俠亖倎偺挿偝偼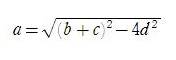 偱偁傞偙偲傪帵偣丅
偱偁傞偙偲傪帵偣丅
拲丗孲忋敧敠恄幮偺栤戣偼俙俛亖們亖俇俉丆俙俢亖倓亖係侽丆俙俠亖倐亖俀俆俈偺偲偒丄俛俠亖倎亖俁侾俆傪帵偡丅
丂
嶲峫暥專丗婒晫導偺嶼妟偺夝愢丂栘廳擵丂挊乮帺旓弌斉乯
奆偝傫丄栤戣傗幙栤偵摎偊偰偔偩偝偄丅堦晹偱傕峔偄傑偣傫偐傜丄夝摎偲儁儞僱乕儉傪揧偊偰丄儊乕儖偱憲偭偰偔偩偝偄丅懸偭偰偄傑偡丅
