—كکaŒ³”N‚VŒژ‚V“ْ
 [—¬‚êگ¯]
[—¬‚êگ¯]
پ@پ@پ@پ@‘و374‰ٌگ”ٹw“I‚ب‰•ه‰ً“ڑ
پ@پ@پ@پ@پƒ‰ً“ڑ•هڈWٹْٹشپF6Œژ9“ْپ`7Œژ7“ْپ„
پmٹEژخپE‘هژخ‚ج’·‚³پn
پ@ٹ°گ3”Nپi1791پj‚ج‘هٹ_ژs‚ج‘هٹ_”ھ”¦‹{‚ة14‘è‚جژZٹz‚ھ•ٍ”[‚³‚ê‚ؤ‚¢‚ـ‚·پB‚»‚ج‚¤‚؟‚ج‘وکZ–â‘è‚ھ‘و‚Uگ}‚إ‚·پB

پ@‚ـ‚½پA‰أ‰i‚R”Nپi1850پj‚ة‚حٹٍ•ŒŒ§ŒSڈمژs‚جŒSڈم”ھ”¦گ_ژذ‚ة‚S‘è‚جژZٹz‚ھ•ٍ”[‚³‚¦‚ؤ‚¢‚ـ‚·پB‚»‚ج‚¤‚؟‚ج‘وˆê–â‘è‚ھ‘و1گ}‚إ‚·پB

’چپFگ}‚إ‚ح’¼ٹpژOٹpŒ`‚ةŒ©‚¦‚ـ‚·‚ھپAژہچغ‚ح‚½‚¾‚جژOٹpŒ`‚ة‚ب‚è‚ـ‚·پB
پ@‚»‚±‚إپAڈم‚ج2‘è‚ًژQچl‚ة‚µ‚ؤپA‰ü‘肵‚ؤڈo‘肵‚ـ‚·پB
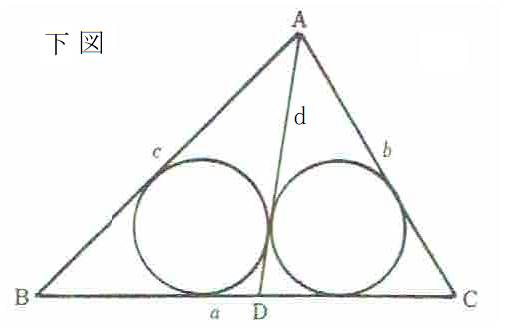
–â‘è‚Pپ@‰؛گ}‚ة‚¨‚¢‚ؤپAپع‚a‚ھ’¼ٹp‚ب’¼ٹpژOٹpŒ`‚`‚a‚b‚ج•س‚a‚b‚ة“ٌ‚آ‚جژOٹpŒ`‚`‚a‚c‚ئ‚`‚b‚c‚ج“àگع‰~‚ج”¼Œa‚ھ“™‚µ‚¢‚و‚¤‚ة“_‚c‚ً‚ئ‚éپB
‚±‚ج‚ئ‚«پAگü•ھ‚`‚cپپ‚„‚ج’·‚³‚حپ@ ‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
پ@’چپF‘هٹ_”ھ”¦‹{‚ج–â‘è‚ح‚a‚bپپaپپ‚P‚TپA‚`‚bپپ‚‚پپ‚P‚VپA‚`‚aپپ‚ƒپپ‚W‚ج‚ئ‚«پA‚`‚cپپ‚„پپ‚P‚O‚ًژ¦‚·پB
–â‘è‚QپA“¯‚¶‰؛گ}‚ة‚¨‚¢‚ؤپAژOٹpŒ`‚`‚a‚b‚ج•س‚a‚b‚ة“ٌ‚آ‚جژOٹpŒ`‚`‚a‚c‚ئ‚`‚b‚c‚ج“àگع‰~‚ج”¼Œa‚ھ“™‚µ‚¢‚و‚¤‚ة“_‚c‚ً‚ئ‚éپB
‚±‚ج‚ئ‚«پAگü•ھ‚a‚bپپ‚پ‚ج’·‚³‚ح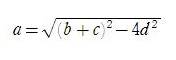 ‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
’چپFŒSڈم”ھ”¦گ_ژذ‚ج–â‘è‚ح‚`‚aپپ‚ƒپپ‚U‚WپC‚`‚cپپ‚„پپ‚S‚OپC‚`‚bپپ‚‚پپ‚Q‚T‚V‚ج‚ئ‚«پA‚a‚bپپ‚پپپ‚R‚P‚T‚ًژ¦‚·پB
پ@
ژQچl•¶Œ£پFٹٍ•ŒŒ§‚جژZٹz‚ج‰ًگàپ@ûü–طڈd”Vپ@’کپiژ©”ïڈo”إپj
NO1پu‘پ‹N‚«‚ج‚¨‚¶‚³‚ٌپv 06/21 17ژ49•ھپ@ژَگM چXگV 7/7
–â‘è1
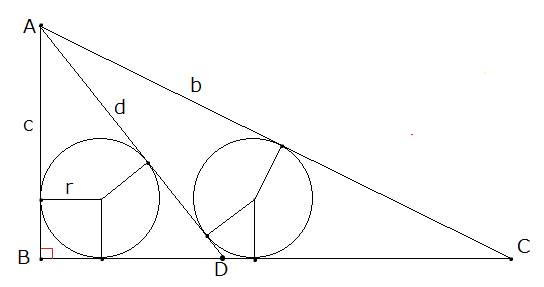
گ}‚ج2‚آ‚ج“àگع‰~‚ج”¼Œa‚ًr‚ئ‚µ‚ـ‚·پB
![]() پA
پA![]() ‚إ‚·پB
‚إ‚·پB
پ¢ABD‚ئپ¢ACD‚ج–تگد‚ً2ژي—ق‚ج•û–@‚إŒvژZ‚µپA”ن‚ً’²‚ׂـ‚·پB
’ê•س‚ًBDپACD‚ئ‚·‚é‚ئپA
![]()
r‚ً—p‚¢‚é‚ئپA
![]()
![]()
‚و‚ء‚ؤپA
![]()
“àچ€‚جگد‚حپA![]()
ٹOچ€‚جگد‚حپA![]()
”نٹr‚µ‚ؤپA
![]()
![]()
![]()
![]()
![]()
![]()
![]()
‰؛گü•”‚ًc‚إگ®—‚·‚é‚ئپA
![]()
![]()
![]()
‚±‚±‚إپAb+dپ‚0پAc+dپ‚0‚ب‚ج‚إپA![]()
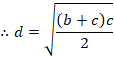
–â‘è2
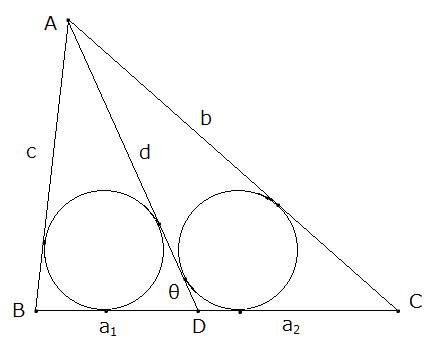
گ}‚إBDپپa1پACDپپa2پAپعADBپپƒئ‚ئ‚µ‚ـ‚·پB
![]()
![]()
‚إ‚·پB
پ¢ABD‚ئپ¢ACD‚ج–تگد‚ج”ن‚حپAa1پFa2‚إ‚·پB
![]()
![]()
(*)‚ً‘م“ü‚µپAگ®—‚·‚é‚ئپA
![]()
پ¢ABD‚و‚èپA
![]()
![]()
پ¢ACD‚و‚èپA
![]()
![]()
![]()
‚و‚ء‚ؤپA
![]()
![]()
(*)‚ً‘م“ü‚µپAگ®—‚·‚é‚ئپA
![]()
![]()
(**)‚ً‘م“ü‚µپAگ®—‚·‚é‚ئپA
![]()
![]()
![]()

‰؛گü•”•ھ‚حپA
![]()
![]()
![]()
![]()
![]()
![]()
‚و‚ء‚ؤپA
![]()
‚±‚±‚إپAaپ‚0پAb+dپ‚0پAc+dپ‚0‚ب‚ج‚إپA
![]()
![]()
NO2پu•l“c–¾–¤پv
06/22 09ژ13•ھپ@ژَگM چXگV 7/7
–â‘è‚P
پ@“àگع‰~‚ج”¼Œa‚ً‚’‚ئ‚·‚é‚ئپC
پ@پ@پ¢‚`‚a‚cپپ‚Pپ^‚QپE‚`‚aپE‚a‚cپپ‚Pپ^‚QپEپi‚`‚aپ{‚a‚cپ{‚`‚c)پE‚’
پ@پ@پˆ‚’پپ{‚ƒپE(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}پ^{‚ƒپ{(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ{‚„}پEپEپE(1)
پ@‚ـ‚½پC
پ@پ@پ¢‚`‚c‚bپپ‚Pپ^‚QپE‚`‚aپE‚a‚bپ|‚Pپ^‚QپE‚`‚aپE‚a‚cپپ‚Pپ^‚QپE(‚`‚cپ{‚c‚bپ{‚`‚b)پE‚’
پ@پ@پˆ‚’پپ{‚پ‚ƒپ|‚ƒپE(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}پ^[‚„پ{{‚پپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}پ{‚‚]
پ@پ@پ@پ@پپ‚ƒ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}پ^{‚‚پ{‚„پ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}پEپEپE(2)
پ@(1)پC(2)پC‚ƒپ‚‚O‚©‚çپC
پ@پ@(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ^{‚ƒپ{‚„پ{(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}
پ@پ@پ@پپ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}پ^{‚‚پ{‚„پ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}
پ@پ@پˆ(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE{‚‚پ{‚„پ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}
پ@پ@پ@پ@پپ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}پE{‚ƒپ{‚„پ{(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Q}
پ@پ@پˆ(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE‚‚پ{(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE‚„پ{(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)
پ@پ@پ@پ@پپ(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE‚ƒپ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE‚„پ{(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE‚ƒ
پ@پ@پ@پ@پ@پ@پ|(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚QپE‚„پ|(‚„‚Qپ|‚ƒ‚Q)
پ@پ@پˆ(‚‚پ{‚ƒپ{‚Q‚„)(‚„‚Qپ|‚ƒ‚Q)‚Pپ^‚Qپپ(‚ƒپ{‚„)(‚‚‚Qپ|‚ƒ‚Q)‚Pپ^‚Q
پ@—¼•س‚ئ‚à”ٌ•‰‚ب‚ج‚إپC
پ@پ@پˆ(‚‚پ{‚ƒپ{‚Q‚„)‚Q(‚„‚Qپ|‚ƒ‚Q)پپ(‚ƒپ{‚„)‚Q(‚‚‚Qپ|‚ƒ‚Q)
پ@پ@پˆ{(‚‚پ{‚ƒ)‚Qپ{‚S(‚‚پ{‚ƒ)‚„پ{‚S‚„‚Q)(‚„‚Qپ|‚ƒ‚Q)پپ(‚ƒ‚Qپ{‚Q‚ƒ‚„پ{‚„‚Q)(‚‚‚Qپ|‚ƒ‚Q)
پ@پ@پˆ(‚‚پ{‚ƒ)‚Q‚„‚Qپ{‚S(‚‚پ{‚ƒ)‚„‚Rپ{‚S‚„‚Sپ|(‚‚پ{‚ƒ)‚Q‚ƒ‚Qپ|‚S(‚‚پ{‚ƒ)‚ƒ‚Q‚„پ|‚S‚ƒ‚Q‚„‚Q
پ@پ@پ@پ@پپ‚ƒ‚Q(‚‚‚Qپ|‚ƒ‚Q)پ{‚Q‚ƒ(‚‚‚Qپ|‚ƒ‚Q)‚„پ{(‚‚‚Qپ|‚ƒ‚Q)‚„‚Q
پ@پ@پˆ‚Q‚„‚Sپ{‚Q(‚‚پ{‚ƒ)‚„‚Rپ{(‚‚پ|‚ƒ)‚ƒ‚„‚Qپ|(‚‚پ{‚ƒ)‚Q‚ƒ‚„پ|‚‚‚ƒ‚Q(‚‚پ{‚ƒ)پپ‚O
پ@پ@پˆ{‚Q‚„‚Qپ|(‚‚پ{‚ƒ)‚ƒ}{‚„‚Qپ|(‚‚پ{‚ƒ)‚„پ{‚‚‚ƒ}پپ‚O
پ@پ@پˆ{‚Q‚„‚Qپ|(‚‚پ{‚ƒ)‚ƒ}(‚„پ|‚‚)(‚„پ|‚ƒ)پپ‚O
پ@ڈًŒڈ‚و‚èپC‚„پ„‚OپC(‚‚پ{‚ƒ)‚ƒپ„‚OپC‚ƒپƒ‚„پƒ‚‚
پ@پ@پˆ‚„پپ[{(‚‚پ{‚ƒ)‚ƒ}پ^‚Q]‚Pپ^‚Q
–â‘è‚Q
پ@‚a‚cپپ‚ک‚ئ‚µپC‚`‚©‚ç‚a‚b‚ةگ‚گü‚`‚g‚ً‰؛‚·‚ئپC
پ@پ@پ¢‚`‚a‚cپپ‚Pپ^‚QپE‚a‚cپE‚`‚gپپ‚Pپ^‚QپE(‚`‚aپ{‚a‚cپ{‚`‚c)پE‚’
پ@پ@پˆ‚کپE‚`‚gپپ(‚ƒپ{‚کپ{‚„)‚’
پ@پ@پˆ‚`‚gپپ(‚ƒپ{‚„پ{‚ک)‚’پ^‚کپEپEپE(1)
پ@‚ـ‚½پC
پ@پ@پ¢‚`‚c‚bپپ‚Pپ^‚QپE‚c‚bپE‚`‚gپپ‚Pپ^‚QپE(‚`‚cپ{‚b‚cپ{‚`‚b)پE‚’
پ@پ@پˆ(‚پپ|‚ک)پE‚`‚gپپ{‚„پ{(‚پپ|‚ک)پ{‚‚}‚’
پ@پ@پˆ‚`‚gپپ(‚پپ{‚‚پ{‚„پ|‚ک)‚’پ^(‚پپ|‚ک)پEپEپE(2)
پ@(1)پC(2)‚©‚çپC
پ@پ@(‚ƒپ{‚„پ{‚ک)پ^‚کپپ(‚پپ{‚‚پ{‚„پ|‚ک)پ^(‚پپ|‚ک)
پ@پ@پˆ(‚ƒپ{‚„پ{‚ک)(‚پپ|‚ک)پپ(‚پپ{‚‚پ{‚„پ|‚ک)‚ک
پ@پ@پˆ‚پ(‚ƒپ{‚„)پ{‚پ‚کپ|(‚ƒپ{‚„)‚کپ|‚ک‚Qپپ(‚پپ{‚‚پ{‚„)‚کپ|‚ک‚Q
پ@پ@پˆ(‚‚پ{‚ƒپ{‚Q‚„)‚کپپ‚پ(‚ƒپ{‚„)
پ@پ@پˆ‚کپپ‚پ(‚ƒپ{‚„)پ^(‚‚پ{‚ƒپ{‚Q‚„)پEپEپE(3)
پ@’¼ٹpژOٹpŒ`‚`‚a‚gپC‚`‚c‚gپC‚`‚b‚g‚ة‚¨‚¢‚ؤپC
پ@پ@‚`‚g‚Qپپ‚`‚a‚Qپ|‚a‚g‚Qپپ‚`‚c‚Qپ|‚c‚g‚Qپپ‚`‚b‚Qپ|‚b‚g‚Q
پ@پ@پˆ‚ƒ‚Qپ|(‚کپ|‚c‚g)‚Qپپ‚„‚Qپ|‚c‚g‚Qپپ‚‚‚Qپ|(‚پپ|‚کپ{‚c‚g)‚Q
پ@‚ƒ‚Qپ|(‚کپ|‚c‚g)‚Qپپ‚„‚Qپ|‚c‚g‚Q‚©‚çپC
پ@پ@‚ƒ‚Qپ|‚ک‚Qپ{‚Q‚c‚gپE‚کپ|‚c‚g‚Qپپ‚„‚Qپ|‚c‚g‚Q
پ@پ@پˆ‚c‚gپE‚Q‚کپپ‚„‚Qپ|‚ƒ‚Qپ{‚ک‚Q
پ@پ@پˆ‚c‚gپپ(‚„‚Qپ|‚ƒ‚Qپ{‚ک‚Q)پ^(‚Q‚ک)پEپEپE(4)
پ@‚„‚Qپ|‚c‚g‚Qپپ‚‚‚Qپ|(‚پپ|‚کپ{‚c‚g)‚Q‚©‚çپC
پ@پ@‚„‚Qپ|‚c‚g‚Qپپ‚‚‚Qپ|(‚پپ|‚ک)‚Qپ|‚Q(‚پپ|‚ک)پE‚c‚gپ|‚c‚g‚Q
پ@پ@پˆ‚c‚gپE‚Q(‚پپ|‚ک)پپ‚‚‚Qپ|(‚پپ|‚ک)‚Qپ|‚„‚Q
پ@پ@پˆ‚c‚gپپ{‚‚‚Qپ|(‚پپ|‚ک)‚Qپ|‚„‚Q}پ^{‚Q(‚پپ|‚ک)}پEپEپE(5)
پ@(4)پC(5)‚©‚çپC
پ@پ@(‚„‚Qپ|‚ƒ‚Qپ{‚ک‚Q)پ^(‚Q‚ک)پپ{‚‚‚Qپ|(‚پپ|‚ک)‚Qپ|‚„‚Q}پ^{‚Q(‚پپ|‚ک)}
پ@پ@پˆ(‚„‚Qپ|‚ƒ‚Qپ{‚ک‚Q)(‚پپ|‚ک)پپ(‚‚‚Qپ|‚پ‚Qپ{‚Q‚پ‚کپ|‚ک‚Qپ|‚„‚Q)‚ک
پ@پ@پˆ‚پ(‚„‚Qپ|‚ƒ‚Q)پ{‚پ‚ک‚Qپ|(‚„‚Qپ|‚ƒ‚Q)‚کپ|‚ک‚Rپپ(‚‚‚Qپ|‚پ‚Qپ|‚„‚Q)‚کپ{‚Q‚پ‚ک‚Qپ|‚ک‚R
پ@پ@پˆ‚پ‚ک‚Qپ{(‚‚‚Qپ|‚پ‚Qپ|‚ƒ‚Q)‚کپ{‚پ(‚ƒ‚Qپ|‚„‚Q)پپ‚O
پ@(3)‚ً‘م“ü‚·‚é‚ئپC
پ@پ@‚پپE‚پ‚Q(‚ƒپ{‚„)‚Qپ^(‚‚پ{‚ƒپ{‚Q‚„)‚Qپ{(‚‚‚Qپ|‚پ‚Qپ|‚ƒ‚Q)پE‚پ(‚ƒپ{‚„)پ^(‚‚پ{‚ƒپ{‚Q‚„)پ{‚پ(‚ƒ‚Qپ|‚„‚Q)پپ‚O
پ@—¼•س‚ةپC(‚‚پ{‚ƒپ{‚Q‚„)‚Qپ^{‚پ(‚ƒپ{‚„)}‚ً‚©‚¯‚é‚ئپC
پ@پ@‚پ‚Q(‚ƒپ{‚„)پ{(‚‚‚Qپ|‚پ‚Qپ|‚ƒ‚Q)(‚‚پ{‚ƒپ{‚Q‚„)پ{(‚ƒپ|‚„)(‚‚پ{‚ƒپ{‚Q‚„)‚Qپپ‚O
پ@پ@پˆ‚پ‚Q(‚ƒپ{‚„)پ{(‚‚‚Qپ|‚ƒ‚Q)(‚‚پ{‚ƒپ{‚Q‚„)پ|‚پ‚Q(‚‚پ{‚ƒپ{‚Q‚„)پ{(‚ƒپ|‚„)(‚‚پ{‚ƒپ{‚Q‚„)‚Qپپ‚O
پ@پ@پˆ‚پ‚Q(‚‚پ{‚„)پپ(‚‚‚Qپ|‚ƒ‚Q)(‚‚پ{‚ƒپ{‚Q‚„)پ{(‚ƒپ|‚„)(‚‚پ{‚ƒپ{‚Q‚„)‚Q
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپ{(‚‚‚Qپ|‚ƒ‚Q)پ{(‚ƒپ|‚„)(‚‚پ{‚ƒپ{‚Q‚„)}(‚‚پ{‚ƒپ{‚Q‚„)
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپ{(‚‚‚Qپ{(‚ƒپ|‚„)‚‚پ{‚„(‚ƒپ|‚Q‚„)}(‚‚پ{‚ƒپ{‚Q‚„)
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپ(‚‚پ{‚„)(‚‚پ{‚ƒپ|‚Q‚„)(‚‚پ{‚ƒپ{‚Q‚„)
پ@پ@پˆ‚پ‚Qپپ(‚‚پ{‚ƒپ|‚Q‚„)(‚‚پ{‚ƒپ{‚Q‚„)پپ(‚‚پ{‚ƒ)‚Qپ|‚S‚„‚Q
پ@Œج‚ة‘èˆس‚حژ¦‚³‚ꂽپD
NO3پuژOٹp’è‹Kپv
07/07 13ژ51•ھپ@ژَگM چXگV 7/7

