令和元年7月７日

[流れ星]

　　　　第375回数学的な応募問題

　　　　＜解答募集期間：７月７日〜８月4日＞

［大小2円の直径の和］

　天保12年（1841）〜弘化2年（1845）に岐阜県不破郡垂井町の南宮大社に9題の算額が奉納されています。そのうちの第7問題が下図です。

題意

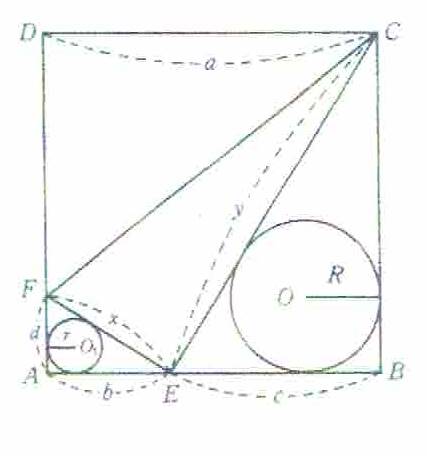
正方形ＡＢＣＤ内に直角三角形ＣＥＦを書き、大小２円Ｏ，Ｏ_１を内接させる。正方形の1辺の長さをａとするとき、大小２円の直径の和を最大にしたい。このとき、直角三角形の二辺の長さを求めよ。ここで、図のようにＡＥ＝ｂ，ＥＢ＝ｃ，ＡＦ＝ｄ，ＥＦ＝ｘ，ＣＥ＝ｙとし，２円Ｏ，Ｏ_１の半径をＲ，ｒとする。

＜水の流れ：微分して解いたのですが。＞

＜参考：関流九伝とは和算の流派の一つ。数学の流派はその研究の対象が数学なので，流派の間の違いはほとんどない。流派によってはほんの少し数式の表し方に違いのあることもある。関流というのは，関孝和の弟子，あるいは孫弟子に教わったという意味である。＞

　

参考文献：岐阜県の算額の解説　��木重之　著（自費出版）

皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。