�ߘa���N�W���S��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��375�����w�I�ȉ����
�@�@�@�@����W���ԁF�V���V���`�W��4����
�m�召2�~�̒��a�̘a�n
�@�V��12�N�i1841�j�`�O��2�N�i1845�j�Ɋ��s�j�S���䒬�̓�{��Ђ�9��̎Z�z����[����Ă��܂��B���̂����̑�7��肪���}�ł��B

���
�����`�`�a�b�c���ɒ��p�O�p�`�b�d�e�������A�召�Q�~�n�C�n�P����ڂ�����B�����`��1�ӂ̒��������Ƃ���Ƃ��A�召�Q�~�̒��a�̘a���ő�ɂ������B���̂Ƃ��A���p�O�p�`�̓�ӂ̒��������߂�B�����ŁA�}�̂悤�ɂ`�d�����C�d�a�����C�`�e�����C�d�e�����C�b�d�����Ƃ��C�Q�~�n�C�n�P�̔��a���q�C���Ƃ���B
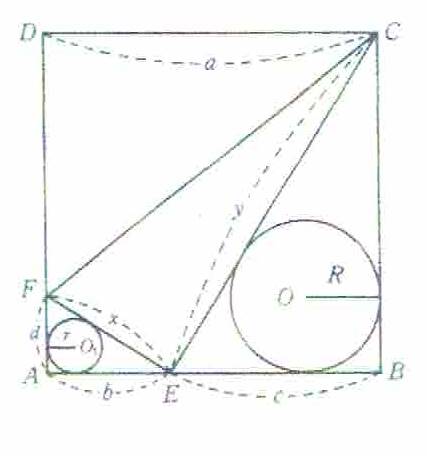
�����̗���F�������ĉ������̂ł����B��
���Q�l�F�֗���`�Ƃ͘a�Z�̗��h�̈�B���w�̗��h�͂��̌����̑Ώۂ����w�Ȃ̂ŁC���h�̊Ԃ̈Ⴂ�͂قƂ�ǂȂ��B���h�ɂ���Ă͂ق�̏��������̕\�����ɈႢ�̂��邱�Ƃ�����B�֗��Ƃ����̂́C�֍F�a�̒�q�C���邢�͑���q�ɋ�������Ƃ����Ӗ��ł����B��
�@
�Q�l�����F���̎Z�z�̉���@���؏d�V�@���i����o�Łj
�u��x�Ђ����v 07/07 22��23���@��M
�X�V 8/4
��375�w�I�ȉ�����̉�
�y���l�[���F��x�Ђ�����
(��)
a=1�Ƃ��čl����悢�D
CE=((CB)^2+(BE)^2)^(1/2)=(1+c^2)^(1/2)�D
R=(CB)*(BE)/(CB+BE+CE)=c/(1+c+(1+c^2)^(1/2))�D
��CBE�Ɓ�EAF�͑����ł���A������́C
CB:EA=1:(1-c)�D
����āCr=(1-c)*R�D
��̉~�̒��a�̘a�́C
2*(R+r)
=2*(2-c)*R
=2*(2-c)*c/(1+c+(1+c^2)^(1/2))
=(2-c)*(1+c-(1+c^2)^(1/2))�D
������,�@(1+c^2)^(1/2)-c=t
�Ƃ����D
c=(1-t^2)/(2*t) �ł���C0<c<1 �Ƃ���C
2^(1/2)-1<t<1�D
2*(R+r)
=(2-c)*(1+c-(1+c^2)^(1/2))
=(4*t-1+t^2)*(1-t)/(2*t)
=5/2-(1/2)*(1/t+3*t+t^2)�D
������w)�����N�E�I�E�E��u��̍ŏ��l���C�������ςƑ��敽�ς�
�ւ���s�������g���ċ��߂�D
1/t+3*t+t^2
=(1/8)*(1/t+1/t+1/t+1/t+1/t+1/t+1/t+1/t
+4*t+4*t+4*t+4*t+4*t+4*t+8*t^2)
��(1/8)*15*((1/t)^8*(4*t)^6*(8*t^2))^(1/15)
=15/4
(�����́Ct=1/2 �̂Ƃ��ɐ�������)
����āC2*(R+r)�́@t=1/2 �̂Ƃ�(c=3/4�̂Ƃ�)�C�ő�ƂȂ�D
���̂Ƃ��C���p�O�p�`CEF�̓�̕�EC�CEF�͂��ꂼ��C
EC=(1+c^2)^(1/2)=5/4�C
EF=(1-c)*EC=5/16�D
���̖��̓����͎��̂悤�ɂȂ�D
�召��̉~�̒��a�̘a���ő�ɂȂ�Ƃ��C
���p�O�p�`�́C���p���͂��ޓ��EC�CEF�̒����́C
EC=(5/4)*a
EF=(5/16)*a
�ł���D
�u���N���̂�������v 07/08 16��26���@��M �X�V 8/4
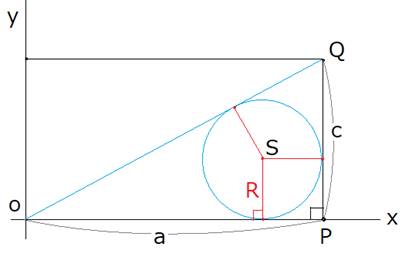
���E�̐}�́A2�ӂ̒�����a�Ac�ł��钼�p�O�p�`�ł��B
���aR�̉~�����ڂ��Ă��܂��B
���aR��a�Ac�ŕ\�����Ƃ��l���܂��B
����OQ�̕������́A![]() �ł��B
�ł��B
���aR�̒��SS�̍��W�́A(a�|R,R)�ł��B
�_S���璼��OQ�܂ł̋�����R�Ȃ̂ŁA
![]()
![]()
![]()
![]()
![]()
![]()
�����ŁA��(+)�̂��̂́A�O�p�`��3�ӂ̘a�ɂȂ�̂ŁA���ډ~�̔��aR�ɂ͂Ȃ�܂���B
![]()
���p�O�p�`�ɓ��ڂ���~�̒��a�̒����́A2�ӂ̘a����Εӂ��������l�ł��B
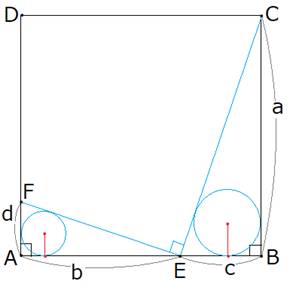 ���̂��Ƃ�p���čl����i�߂܂��B
���̂��Ƃ�p���čl����i�߂܂��B
�����p�O�p�`BCE��AEF�ɓ��ڂ���2�̉~�̒��a�̘aW�́A
![]()
�������Ac�́A0��c��a�͈̔͂ł��B
�����ŁA
![]()
�Ȃ̂ŁA
![]()
�����W�́A
![]()

![]()
![]()
![]()
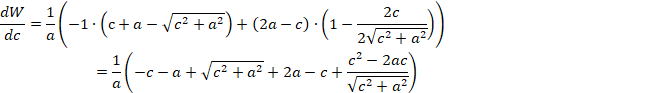
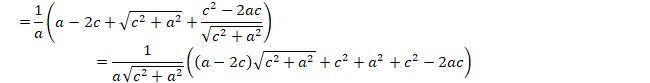
![]()
![]()
![]()
�����ŁA�������͐��ł��B
����āAW�̓�����0�̂Ƃ��́A
![]()

![]()
![]()
�����\�͎��̂悤�ɂȂ�܂��B
 �ȏォ��A
�ȏォ��A
���p�O�p�`BCE��2�ӂ́A![]() ��
�� ![]()
���p�O�p�`AEF��2�ӂ́A![]() ��
�� ![]()
�u�l�c�����v
08/05 14��55���@��M �X�V 8/5
���l�c����̃R�����g�F���ߐ��ł����A���e�҂����Ȃ��悤�ł����A������A�v���[�`�ŁB��
���`�d�e�C���a�b�d�ɂ����āC
�@�@�d�e�Q���`�d�Q�{�`�c�Q�C�b�d�Q���a�b�Q�{�a�d�Q
�@�@������(���Q�{���Q)�P�^�Q�C����(���Q�{���Q)�P�^�Q
�@�܂��C���a�b�d�ɂ����āC
�@�@�b�d��(�a�d�|�q)�{(�a�b�|�q)�����{���|�Q�q
�@�@��(���{���|�Q�q)�Q�����Q�{���Q
�@�@���Q�����|�S(���{��)�q�{�S�q�Q���O
�@�@���Q�q�Q�|�Q(���{��)�q�{�������O
�@�q�����{�����C
�@�@�q��{(���{��)�|(���Q�{���Q)�P�^�Q}�^�Q
�@���l�ɁC����{(���{��)�|(���Q�{���Q)�P�^�Q}�^�Q
�@�@���Q(�q�{��)��(���{���{���{��)�|(���Q�{���Q)�P�^�Q�|(���Q�{���Q)�P�^�Q
�@�@�@�@�@�@�@�@��(�Q���{��)�|(���Q�{���Q)�P�^�Q�|(���Q�{���Q)�P�^�Q
�@���b�c�e�ɂ����āC�b�c�Q�{�c�e�Q���b�e�Q
�@�@�����Q�{(���|��)�Q���d�e�Q�{�b�d�Q��(���Q�{���Q)�{(���Q�{���Q)
�@�@�����Q�|�Q���������Q�{(���|��)�Q
�@�@�����Q�|�����{�������O
�@���������C
�@�@����(���|(���Q�|�S����)�P�^�Q}�^�Q
�@�@�����Q�{���Q��{���Q�|�Q��(���Q�|�S����)�P�^�Q�{(���Q�|�S����)}�^�S�{���Q
�@�@�@�@�@�@�@�@���P�^�Q�E���Q�|�P�^�Q�E��(���Q�|�S����)�P�^�Q�|�����{���Q�C
�@�@�@���Q�{���Q�����Q�{(���|��)�Q
�@�@�@�@�@�@�@�@�����Q�{[{���{(���Q�|�S����)�P�^�Q}�^�Q]�Q
�@�@�@�@�@�@�@�@�����Q�{{���Q�{�Q��(���Q�|�S����)�P�^�Q�{(���Q�|�S����)}�^�S
�@�@�@�@�@�@�@�@���R�^�Q�E���Q�{�P�^�Q�E��(���Q�|�S����)�P�^�Q�|����
�@�@���Q(�q�{��)���Q���{���|{�R�^�Q�E���Q�{�P�^�Q�E��(���Q�|�S����)�P�^�Q�|����}�P�^�Q
�@�@�@�@�@�@�@�@�@�@�|{�P�^�Q�E���Q�|�P�^�Q�E��(���Q�|�S����)�P�^�Q�|�����{���Q}�P�^�Q
�@�����ŁC���^�������C��(��)���Q(�q�{��)�^���Ƃ���ƁC
�@�@��(��)���Q�{���|{�R�^�Q�{�P�^�Q�E(�P�|�S��)�P�^�Q�|��}�P�^�Q
�@�@�@�@�@�@�@�|{�P�^�Q�|�P�^�Q�E(�P�|�S��)�P�^�Q�|���{���Q}�P�^�Q
�@�܂��C�O�������P�^�S�ƂȂ�D
�@�O���t�\���\�t�g�f�q�`�o�d�r���g���C�ŏI�I�ɂ͂P�O�|�P�T�����݂Œ��ׂ����ʁC
�@�@�����O.�P�W�V�T���R�^�P�U
�̂Ƃ��C��(��)�͍ő�ƂȂ�D
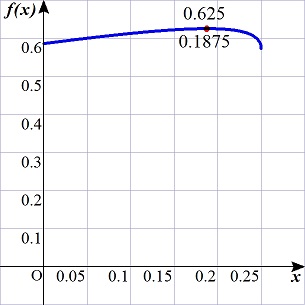
���̂Ƃ��C�����R�^�P�U�E��
�@�@������{���|(���Q�|�S����)�P�^�Q}�^�Q��{���|(���Q�|�R�^�S�E���Q)�P�^�Q}�^�Q�����^�S�C
�@�@�@�������|�����R�^�S�E��
�@�@������(���Q�{���Q)�P�^�Q��(���Q�^�P�U�{�X�^�P�U
�@�@�@����(���Q�{���Q)�P�^�Q��(���Q�{�X�^�P�U�E���Q)�P�^�Q���T�^�S�E��
�@�̂ɁC�������^�S�C�����R�^�S�E���C�����R�^�P�U�E���̂Ƃ��C�����T�^�P�U�E���C�����T�^�S�E���ƂȂ�D
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
