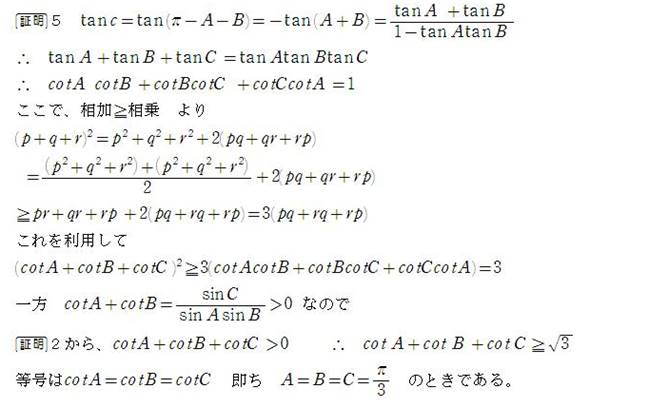令和元年８月４日

[流れ星]

　　　　第376回数学的な応募問題

　　　　＜解答募集期間：８月４日〜９月１日＞

［△ABCのcot不等式］

　

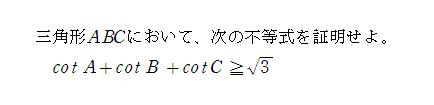
＜水の流れ：数種類の証明方法があります。複数の証明方法で解けた実感を味わっていただければ幸いです。＞

NO1「浜田明巳」 08/05 17時53分　受信 更新 9/1

cotＡ＋cotＢ＋cotＣ≧√３

　Ａ＋Ｂ＋Ｃ＝πから，cot(Ａ＋Ｂ)＝cot(π−Ｃ)
　　∴(cosＡcosＢ−sinＡsinＢ)／(sinＡcosＢ＋cosＡsinＢ)＝１／tan(π−Ｃ)
　　∴(cotＡcotＢ−１)／(cotＢ＋cotＡ)＝−１／tanＣ
　　∴cotＡcotＢ−１＝−cotＣ(cotＡ＋cotＢ)
　　∴cotＡcotＢ＋cotＢcotＣ＋cotＣcotＡ＝１・・・(1)

　ここで，
　　(cotＡ＋cotＢ＋cotＣ)^２−３
　　　＝(cot^２Ａ＋cot^２Ｂ＋cot^２Ｃ＋２cotＡcotＢ＋２cotＢcotＣ＋２cotＣcotＡ)−３
　　　＝cot^２Ａ＋cot^２Ｂ＋cot^２Ｃ−１（∵(1)）
　　　＝cot^２Ａ＋cot^２Ｂ＋cot^２Ｃ−(cotＡcotＢ＋cotＢcotＣ＋cotＣcotＡ)（∵(1)）
　　　＝１／２・{(cotＡ−cotＢ)^２＋(cotＢ−cotＣ)^２＋(cotＣ−cotＡ)^２}≧０
　　∴(cotＡ＋cotＢ＋cotＣ)^２≧３・・・(2)

　cotＡ＋cotＢ＋cotＣ＜０と仮定する．
　　cotＢ＋cotＣ＜−cotＡ＝−cot{π−(Ｂ＋Ｃ)}＝cot(Ｂ＋Ｃ)＝(cotＢcotＣ−１)／(cotＢ＋cotＣ)
　cotＢ＋cotＣ＞０と仮定すると，
　　(cotＢ＋cotＣ)^２＜cotＢcotＣ−１
　　∴cot^２Ｂ＋cotＢcotＣ＋cot^２Ｃ＜−１・・・(3)
　ここで，
　　cot^２Ｂ＋cotＢcotＣ＋cot^２Ｃ＝(cotＢ＋１／２・cotＣ)^２＋３／４・cot^２Ｃ≧０
　これは(3)に矛盾する．
　　∴cotＢ＋cotＣ＜０
　　∴cotＢ≦０またはcotＣ≦０
　 　故に∠Ｂまたは∠Ｃは直角または鈍角である．
　故に∠Ａは鋭角である．
　同様にして，cotＣ＋cotＡ＜０，cotＡ＋cotＢ＜０から，∠Ｂ，∠Ｃは鋭角である．
　∠Ａ，∠Ｂ，∠Ｃのすべてが鋭角となり，cotＡ＞０，cotＢ＞０，cotＣ＞０
　これは，cotＡ＋cotＢ＋cotＣ＜０に反する．
　　∴cotＡ＋cotＢ＋cotＣ≧０
　(2)より，cotＡ＋cotＢ＋cotＣ≧√３
＜水の流れ：cotＡ＋cotＢ＋cotＣ≧０　で実際は>０です。等号の０は起こらないです＞

これに対して、返事が以下です。しかし、後で、子細なことで反省しました。

「浜田明巳」 08/06 19時01分　受信 更新 9/1

（追加）

　証明の流れは，まず，

　　(cotＡ＋cotＢ＋cotＣ)２≧３

を示す．

　cotＡ＋cotＢ＋cotＣ＜０と仮定すると，矛盾することから．

　　cotＡ＋cotＢ＋cotＣ≧０

　　∴cotＡ＋cotＢ＋cotＣ≧√３

　したがって，cotＡ＋cotＢ＋cotＣ＝０の場合が存在するかどうか，確かめなくてよいわけです．

　だから，cotＡ＋cotＢ＋cotＣ≦０と仮定して，矛盾を示し，cotＡ＋cotＢ＋cotＣ＞０としなかっただけです．

　また，証明の最後に等号が成立する，すなわち，cotＡ＋cotＢ＋cotＣ＝√３となる場合について，述べる必要はありません．

　問題に要求されていないからです．

　よけいな事を書いて，そこで間違って，減点されてもつまらない．

　しかし，入試の解答では，

　　cotＡ−cotＢ＝cotＢ−cotＣ＝cotＣ−cotＡ＝０

　すなわち，

　　cotＡ＝cotＢ＝cotＣ

となり，∠Ａ＝∠Ｂ＝∠Ｃ

　よって，△ＡＢＣは正三角形のとき，等号成立としておいた方がよいでしょう．

　古めかしい考えの採点者に当たった場合，減点されてしまうかも知れません．

　受験者は採点者を選べない．

「浜田明巳」 08/07 18時50分　受信 更新 9/1

（別解その１）
　∠Ａを最大角とすると，０＜∠Ｂ＜π／２，０＜∠Ｃ＜π／２
　Ａから辺ＢＣに垂線ＡＨを下ろすと，
　　cotＢ＝ＢＨ／ＡＨ，cotＣ＝ＣＨ／ＡＨ
　　∴cotＢ＋cotＣ＝ＢＣ／ＡＨ
　また，
　　cotＡ＝cot{π−(Ｂ＋Ｃ)}＝−cot(Ｂ＋Ｃ)
　　　　　＝(１−cotＢcotＣ)／(cotＢ＋cotＣ)
　　　　　＝{１−(ＢＨ・ＣＨ)／ＡＨ^２}／(ＢＣ／ＡＨ)
　　　　　＝ＡＨ／ＢＣ−(ＢＨ・ＣＨ)／(ＢＣ・ＡＨ)
　ここで，ＢＣ＝ａ，ＡＨ＝ｈ，ＢＨ＝ｋａ，０＜ｋ＜１とすると，
　　cotＡ＋cotＢ＋cotＣ＝ｈ／ａ−{ｋａ・(１−ｋ)ａ}／(ａｈ)＋ａ／ｈ
　　　　　　　　　　　　＝ｈ／ａ＋ａ／ｈ・(ｋ^２−ｋ＋１)
　ｘ＝ａ／ｈとすると，
　　与式＝(ｋ^２−ｋ＋１)ｘ＋１／ｘ
　(ｋ^２−ｋ＋１)ｘ＞０，１／ｘ＞０より，相加平均と相乗平均の関係から，
　　与式≧２(ｋ^２−ｋ＋１)^１／２
　ｆ(ｋ)＝ｋ^２−ｋ＋１とすると，０＜ｋ＜１より，
　　ｆ(ｋ)＝(ｋ−１／２)^２＋３／４≧３／４（ｆ(１／２)＝３／４）
　　∴与式≧２(３／４)^１／２＝√３
　故に題意は示された．
　念の為に，等号が成立する場合を調べる．
　(ｋ^２−ｋ＋１)ｘ＝１／ｘ，ｋ＝１／２より，
　　ｘ^２＝４／３
　ｘ＞０から，
　　ｘ＝２／√３＝ａ／ｈ
　　∴ｈ＝√３／２・ａ
　　∴ＡＨ＝√３／２・ＢＣ
　また，ＢＨ＝ＣＨ＝ａ／２
　故に△ＡＢＣは正三角形である．

「浜田明巳」 08/08 19時15分　受信 更新 9/1

（別解その２）
　∠Ａを最大角とすると，０＜∠Ｂ＜π／２，０＜∠Ｃ＜π／２
　座標系を導入する．
　Ｂ(０，０)，Ｃ(ａ，０)，Ａ(ｂ，ｃ)，０＜ｂ＜ａ，ｃ＞０とすると，
　　cotＢ＝ｂ／ｃ，cotＣ＝(ａ−ｂ)／ｃ
　　∴cotＢ＋cotＣ＝ａ／ｃ
　また，
　　cotＡ＝−cot(Ｂ＋Ｃ)＝(１−cotＢcotＣ)／(cotＢ＋cotＣ)
　　　　　＝{１−(ｂ／ｃ)・(ａ−ｂ)／ｃ}／(ａ／ｃ)
　　　　　＝ｃ／ａ−{ｂ(ａ−ｂ)}／(ａｃ)
　　∴左辺＝ｃ／ａ＋ａ／ｃ−{ｂ(ａ−ｂ)}／(ａｃ)
　ここで，ｂ＝ａｋ，０＜ｋ＜１とすると，
　　左辺＝ｃ／ａ＋ａ／ｃ−{ａｋ・(１−ｋ)ａ}／(ａｃ)
　　　　＝ｃ／ａ＋ａ／ｃ・(１−ｋ＋ｋ^２)
　以下，別解その１と同様．

（別解その３）
　∠Ｃを最大角とすると，cotＡ＞０，cotＢ＞０
　このとき，
　　cotＡ＋cotＢ＋cotＣ＝cotＡ＋cotＢ−cot(Ａ＋Ｂ)
　　　＝cotＡ＋cotＢ＋(１−cotＡcotＢ)／(cotＡ＋cotＢ)
　　　＝{(cotＡ＋cotＢ)^２＋(１−cotＡcotＢ)}／(cotＡ＋cotＢ)
　　　＝(cot^２Ａ＋cotＡcotＢ＋cot^２Ｂ＋１)／(cotＡ＋cotＢ)
　ここで，ｘ＝cotＡ，ｙ＝cotＢとし，
　　ｆ(ｘ，ｙ)＝(cot^２Ａ＋cotＡcotＢ＋cot^２Ｂ＋１)−√３・(cotＡ＋cotＢ)
　　　　　　　＝ｘ^２＋ｙ^２＋ｘｙ−√３・ｘ−√３・ｙ＋１
とすると，
　　ｆ(ｘ，ｙ)＝ｘ^２＋(ｙ−√３)ｘ＋(ｙ^２−√３・ｙ＋１)
　　　　　　　＝{ｘ＋(ｙ−√３)／２}^２−１／４・(ｙ^２−２√３・ｙ＋３)＋(ｙ^２−√３・ｙ＋１)
　　　　　　　＝{ｘ＋(ｙ−√３)／２}^２＋３／４・ｙ^２−√３／２・ｙ＋１／４
　　　　　　　＝{ｘ＋(ｙ−√３)／２}^２＋(√３／２・ｙ−１／２)^２≧０
　等号は，ｘ＋(ｙ−√３)／２＝√３／２・ｙ−１／２＝０，すなわち，ｘ＝ｙ＝１／√３のとき，成立する．
　　∴ｆ(ｘ，ｙ)＝(cot^２Ａ＋cotＡcotＢ＋cot^２Ｂ＋１)−√３・(cotＡ＋cotＢ)≧０
　cotＡ＋cotＢ＞０より，
　　(cot^２Ａ＋cotＡcotＢ＋cot^２Ｂ＋１)／(cotＡ＋cotＢ)≧√３
　　∴cotＡ＋cotＢ＋cotＣ≧√３
　等号が成立するとき，cotＡ＝cotＢ＝１／√３
　　∴∠Ａ＝∠Ｂ＝π／３
　故に△ＡＢＣは正三角形である．

（別解その４）
　ｆ(ｘ，ｙ)＝ｘ^２＋ｙ^２＋ｘｙ−√３・ｘ−√３・ｙ＋１より，
　　ｆ_ｘ＝２ｘ＋ｙ−√３
　　ｆ_ｙ＝２ｙ＋ｘ−√３
　ここで，ｆ_ｘ＝ｆ_ｙ＝０とすると，
　　２ｘ＋ｙ＝√３，ｘ＋２ｙ＝√３
　　∴ｘ＝ｙ＝１／√３
　また，ｆ(１／√３，１／√３)＝１／３＋１／３＋１／３−１−１＋１＝０
　　lim_ｘ→∞ｆ(ｘ，ｙ)＝∞，lim_ｙ→∞ｆ(ｘ，ｙ)＝∞
　故にｆ(ｘ，ｙ)は，ｘ＝ｙ＝１／√３のとき，極小，かつ最小．
　以下，別解その３と同様．

NO2「二度漬け白菜」 08/18 11時35分　受信 更新 9/1

[解答]
三角形ABCにおいて
cot(A)+cot(B)+cot(C)≧3^(1/2)
が成り立つ．

(証明)
三角形ABCを，xy直交座標に置いて考える．
A,B,Cの座標をそれぞれ
A(0,0)，B(1,0)，C(x,y) (ただし，y>0)
と設定する．
三角形ABCの面積をSとすると，S = y/2 である．

余弦定理より，
-a^2+b^2+c^2=2*b*c*cos(A)=2*b*c*sin(A)*cot(A)=4*S*cot(A)．
つまり，
-a^2+b^2+c^2 = 4*S*cot(A) --- (1)
が成り立っている．

同様に，余弦定理を適用することによって，
a^2-b^2+c^2 = 4*S*cot(B) --- (2)
a^2+b^2-c^2 = 4*S*cot(C) --- (3)
を得る．

(1),(2),(3) の辺々を加えて，
a^2+b^2+c^2 = 4*S*(cot(A)+cot(B)+cot(C))．

よって，
cot(A)+cot(B)+cot(C)
=(a^2+b^2+c^2)/(4*S)
=(x^2-x+1+y^2)/y
=3^(1/2) + ((x-1/2)^2)/y + ((3/(4*y))^(1/2)-y^(1/2))^2
≧3^(1/2)．
(等号は x=1/2 かつ y=(3/4)^(1/2) のときのみ成り立つ)

以上より，不等式
cot(A)+cot(B)+cot(C)≧3^(1/2)
が成り立つことを示せた．
等号が成立するのは 三角形ABCが正三角形のときだけである．(証明終)



(別解)
A≦B≦C と仮定しても一般性を失わない．
0＜A≦B＜π/2 であるから sin(A),cos(A),sin(B),cos(B)の値はすべて正である．

cot(A)=X, cot(B)=Y とおく．

cot(C)
=cos(C)/sin(C)
=cos(Π-(A+B))/sin(Π-(A+B))
=-cos(A+B)/sin(A+B)
=sin(A)*sin(B)/sin(A+B) - cos(A)*cos(B)/sin(A+B)
=1/(sin(A+B)/sin(A)*sin(B)) - 1/(sin(A+B)/cos(A)*cos(B))
=1/((cos(A)/sin(A))+(cos(B)/sin(B))) - 1/((sin(A)/cos(A))+(sin(B)/cos(B)))
=1/(X+Y) - 1/(1/X + 1/Y)
=(1-X*Y)/(X+Y).

よって，
cot(A)+cot(B)+cot(C)
=X+Y+(1-X*Y)/(X+Y)
=((3*(X+Y)/4)^(1/2)-(1/(X+Y))^(1/2))^2 + (1/4)*((X-Y)^2)/(X+Y) + 3^(1/2)
≧3^(1/2).
(等号は (3*(X+Y)/4)^(1/2)=(1/(X+Y))^(1/2) かつ X=Y のときのみ，
すなわち X=Y=3^(-1/2) のときのみ成立)


---------------------------------------------------

今回の問題の不等式 cot(A)+cot(B)+cot(C)≧3^(1/2) は，
次の不等式と同値です．

a^2+b^2+c^2≧4*3^(1/2)*S  ---(★)

(★)を，「Weitzenbockの不等式」と言うそうです．
多くの証明が知られているようです．
https://math.stackexchange.com/questions/2143589/proofs-of-the-weitzenbock-inequality-a2b2c2-geq-4-sqrt3-cdot-textare


また，任意の三角形ABCと任意の自然数 n に対して，不等式
(cot(A))^n + (cot(B))^n + (cot(C))^n ≧ 3*3^(-n/2)　---(★★)
か成り立ちます．
下記ファイル 37頁の 2.65
https://www.isinj.com/mt-usamo/Geometric%20Inequalities%20-%20Bottema,%20et.%20al.%20(1968).pdf

(証明)
A≦B≦Cとしても一般性を失わない．
|cot(A)|≧|cot(B)|≧|cot(C)|であるから
任意の自然数 n に対して
(cot(A))^n≧(cot(B))^n≧(cot(C))^n.

n=1のときには(★★)は成り立つ．
n=kのときに(★★)が成り立つと仮定する．
チェビシェフの不等式により，
(cot(A))^(k+1)+(cot(B))^(k+1)+(cot(C))^(k+1)
≧((cot(A))^k+(cot(B))^k+(cot(C))^k)*(cot(A)+cot(B)+cot(C))/3
≧ (3*3^(-k/2))*(3^(1/2))/3
=3*3^(-(k+1)/2).
よってn=k+1のときにも(★★)は成り立つ．(終)

(以上)

＜水の流れ：いろんなことが勉強になり、凄く感謝しています＞

NO3「早起きのおじさん」 08/22 17時41分　受信 更新 9/1

●「cot」について、確認しておきます。

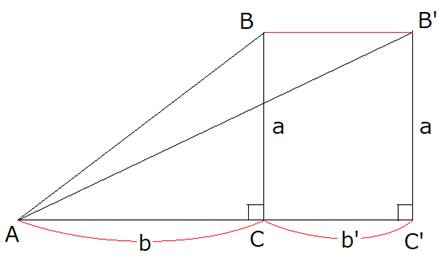
直角三角形ABCで、

直角三角形AB’C’で、

鋭角のとき、「cot」は角が小さくなると、値が大きくなります。

●三角形が鋭角三角形のときは、三角比の値が正です。

3個の数が正のとき、相加平均と相乗平均の関係から次の不等式が成立します。

等号は、3個の数がすべて等しいときです。

つまり、 のときです。

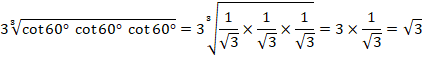
よって、

○次に直角三角形のときをみてみます。

とします。

○さらに鈍角三角形のときをみてみます。

とします。

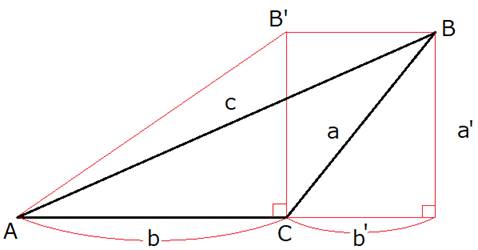
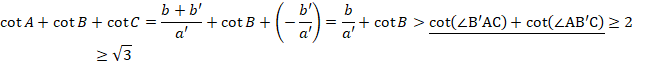
下線部分は、直角三角形AB’Cを考えています。

●別の方法考えます。

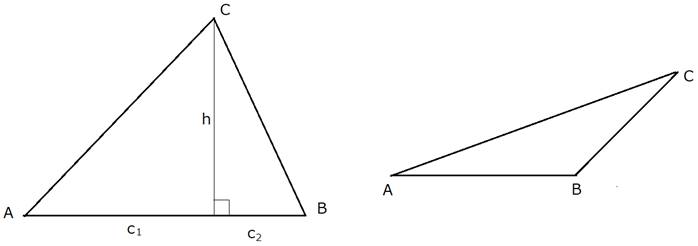
上の図で、 とおきます。

と はお互い関係がないので、 は正の実数の値を自由にとれます。

(AかB)が鈍角になるような場合は、辺ACが水平になるように三角形を置き直し(AかB)とCの名前を入れ替えます。

（あるいは、上でみたように直角三角形や鈍角三角形の場合、「cot」の値の和は、2以上なので考慮の必要がないとします）

ここで、 とおきます。

x、yは正と考えます。

分母が正なので、分子＝0とすると、

(yは正なので)

このyでzは極小値をとるので、zに入れると、

分母が正なので、分子＝0とすると、

より、

このxで極小値をとるので、zに入れると、

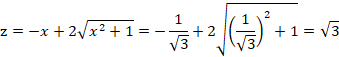
「早起きのおじさん」 08/29 16時29分　受信 更新 9/1

●直線m、nの幅は1とします。

〇先ず正三角形で様子をみます。

△ABCの辺ACをm上に置きます。

ABとnとの交点から、mに垂線を下ろします。(垂線の足X)

すると、AX=cotAです。

△ABCを左に回転し、Xに頂点Bを重ね、辺BAをm上に置きます。

BCとnとの交点から、mに垂線を下ろします。(垂線の足Y)

すると、BY=cotBです。

△ABCを左に回転し、Yに頂点Cを重ね、辺CBをm上に置きます。

CAとnとの交点から、mに垂線を下ろします。(垂線の足Z)

すると、CZ=cotCです。

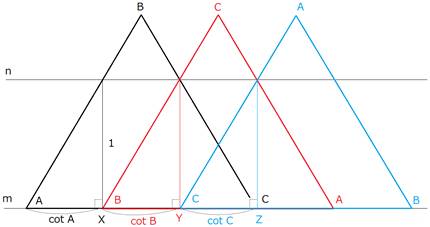
はすぐにわかります。

〇次に一般の三角形でやってみます。

(この例は、∠Aは60°より小さく、∠Ｂ、∠Ｃは60°より大きいとします)

△ABCの辺ACをm上に置きます。

ABとnとの交点から、mに垂線を下ろします。(垂線の足X)

すると、AX=cotAです。

△ABCを左に回転し、Xに頂点Bを重ね、辺BAをm上に置きます。

BCとnとの交点から、mに垂線を下ろします。(垂線の足Y)

すると、BY=cotBです。

△ABCを左に回転し、Yに頂点Cを重ね、辺CBをm上に置きます。

CAとnとの交点から、mに垂線を下ろします。(垂線の足Z)

すると、CZ=cotCです。

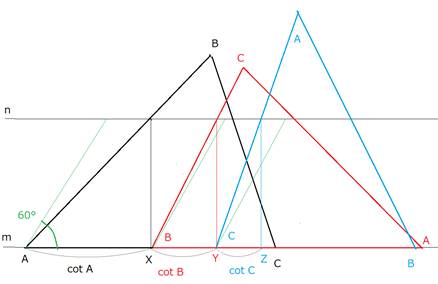
〇さて、図の黄緑の線は、正三角形を置いたときのものです。

∠Aは60°より小さいので、cotAはcot60°より大きいです。

∠B、∠Cは60°より大きいので、cotB、cotCはcot60°より小さいです。

〇以下、上の例の定性的な説明をします。

三角形の内角の和は、一定です。(180°)

60°より小さい角の60°より小さい分θと、60°より大きい角の60°より大きい分の和は等しくなります。

∠Aは60°よりθ小さいとします。

∠B、∠Cは60°より大きいのですが、合計すると、60°よりθ大きくなります。

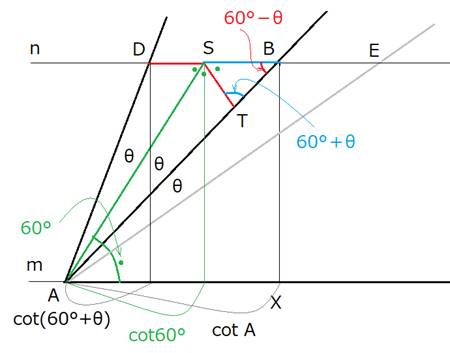
図のような△STBを考えます。

SBはcotAがcot60°より大きい分です。（SB＝cotA−cot60°）

ST(＝SD)はcot(60°＋θ)がcot60°より小さい分です。(ST＝cot60°−cot(60°＋θ))

SBの対角は60°＋θ、STの対角は60°−θなので、SB＞ST(＝SD)

つまり、三角形の内角が60°より小さくなったことでcot60°より大きくなった「cot」の増加分SBは、

60°より大きいことでcot60°より小さくなった「cot」の減少分STより大きいのです。

もし三角形の内角が、60°−θ、60°、60°＋θなら、「cot」の和は、SB−SDの分大きくなります。

内角がさらにもうθ小さくなると、上の図のさらにBEの分「cot」の値が大きくなります。

〇角が小さくなるにつれ増加分は増えていき、角が大きくなるにつれて減少分は減っていきます。

正三角形からずれればずれるほど、「cot」の和は、大きくなっていきます。

「早起きのおじさん」 08/30 17時04分　受信 更新 9/1

●おまけ

微分の感覚で見てみます。

直角三角形OABの2辺の長さは、1とcotθです。

斜辺は です、。

これは、 の両辺を正弦(sin)の2乗で割った式を考えるとわかりやすいです。

図のACが角の微小変量dθに対する余接(cot)の微小変量d(cotθ)です。

向きを考えて(左を「−」とします)、−d(cotθ)とします。

ADは、 、 です。

直角三角形CADより、

これは、「cot」の導関数です。

微小変量は、

この式は、「cot」は角θが小さい方が微小変量の絶対値が大きくなることを示しています。

これは、前回の解答を裏付けています。

NO4　水の流れ　準備していた解答です。