�ߘa���N10��27��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��378�����w�I�ȉ����
�@�@�@�@����W���ԁF9��29���`10��27����
�m���̑��ݔ͈́n
�@
�@���u�ЍH�w���̉ߋ���ŁA�ꕔ���肵�Ă���܂��B

NO1�u�X���[�N�}���v 10/02 20��42���@��M
�X�V 10/27
(���1)
x^2-1=a(x-��2) ����A
�E�̒����� (��2,0)��ʂ�̂�...
���炩�ɁA0<=a �ŁA
y=x^2-1 �� y=a(x-��2)�̐ڐ��̏������X����a�܂�...
x^2-ax=1-a��2
(x-a/2)^2=1-a��2+a^2/4>=0
a^2-4��2*a+4>=0
(a-2��2)^2>=-4+8=4
so...
a=2��2-2 �̕�
so...
0<=a<=2��2-2
�u�X���[�N�}���v 10/04 13��49���@��M
�X�V 10/27
(���2)�̉ł�...
���܂����A�Ƃ������A��������...^^;;
��(1-x^2)*��(1-y^2)=x+y
y=x�Ɋւ��đΏ�
x=0,y=��2/2
x=y,x=y=��2-1
x=0〜��2-1�܂ŁA�O���t�͘A��
x�Ŕ���������c
-x��(1-y^2)/��(1-x^2)-1�ƕ��ɂȂ�̂��c
��ɓʂ̋Ȑ��ɂȂ邵���Ȃ��c
���ۂ̐}���c
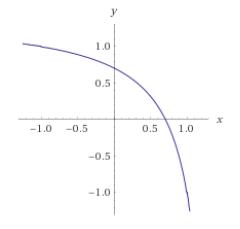
x+y=t �ct��x,y�ؕ�
so�c
��2/2<t<=��2(��2-1)=2-��2
�X�}�[�g����Ȃ��Ȃ��c^^;
NO2�u�l�c�����v
10/03 16��09���@��M �X�V 10/27
���P�i�O���t���g���ă`�}�`�}���͖̂ʓ|�D�v�Z�ŃS���S�������܂��D�͖̂����������C�����s�����́C�O���t���g�킸�C�v�Z�����ʼn��������̂ł��j
�@�@���Q�|�����{���Q���|�P���O�E�E�E(1)
(1)�̔��ʎ����c�Ƃ���ƁC���͎����Ȃ̂ŁC
�@�@�c�����Q�|�S(���Q���|�P)�����Q�|�S���Q���{�S���O
�@�@�������Q���Q�|�Q�C�Q���Q�{�Q�����E�E�E(2)
�@���̂Ƃ��C(1)�̉��́C
�@�@����{���}(���Q�|�S���Q���{�S)�P�^�Q}�^�Q
i). �|�P��{���{(���Q�|�S���Q���{�S)�P�^�Q}�^�Q���P�̂Ƃ��C
�@�@�|�Q�����{(���Q�|�S���Q���{�S)�P�^�Q���Q
�@�@���|���|�Q��(���Q�|�S���Q���{�S)�P�^�Q���Q�|��
�@�A). (���Q�|�S���Q���{�S)�P�^�Q���Q�|������C
�@�@�@�O��(���Q�|�S���Q���{�S)�P�^�Q���Q�|��
�@�@�@���O���Q�|��
�@�@�@�������Q
�@�@(2)����C�����Q���Q�|�Q�E�E�E(3)
�@�@���̂Ƃ��C�O��(���Q�|�S���Q���{�S)�P�^�Q���Q�|������C
�@�@�@���Q�|�S���Q���{�S��(�Q�|��)�Q
�@�@�@���S(�P�|���Q)�����O
�@�@�@�������O
�@�@(3)����C�O�������Q���Q�|�Q�E�E�E(4)
�@�C). �|���|�Q��(���Q�|�S���Q���{�S)�P�^�Q�ɂ����āC
�@�@(4)����C�|�����O
�@�@�@���|���|�Q���O��(���Q�|�S���Q���{�S)�P�^�Q
�@�@����͏�ɐ�������D
�@�܂Ƃ߂�ƁC�O�������Q���Q�|�Q
ii). �|�P��{���|(���Q�|�S���Q���{�S)�P�^�Q}�^�Q���P�̂Ƃ��C
�@�@�|�Q�����|(���Q�|�S���Q���{�S)�P�^�Q���Q
�@�@�����|�Q��(���Q�|�S���Q���{�S)�P�^�Q�����{�Q
�@�A). (���Q�|�S���Q���{�S)�P�^�Q�����{�Q����C
�@�@�@�O��(���Q�|�S���Q���{�S)�P�^�Q�����{�Q
�@�@�@���O�����{�Q
�@�@�@�������|�Q
�@�@(2)����C�|�Q�������Q���Q�|�Q�C�Q���Q�{�Q�����E�E�E(5)
�@�@���̂Ƃ��C�O��(���Q�|�S���Q���{�S)�P�^�Q�����{�Q����C
�@�@�@���Q�|�S���Q���{�S��(���{�Q)�Q
�@�@�@���S(�|�P�|���Q)�����O
�@�@�@�������O
�@�@(5)����C�O�������Q���Q�|�Q�C�Q���Q�{�Q�����E�E�E(6)
�@�C). ���|�Q��(���Q�|�S���Q���{�S)�P�^�Q�ɂ����āC
�@�@�P). ���|�Q���O�̂Ƃ��C�����Q
�@�@�@(6)����C�O�������Q���Q�|�Q�E�E�E(7)
�@�@�@���̂Ƃ��C���|�Q���O��(���Q�|�S���Q���{�S)�P�^�Q�͏�ɐ�������D
�@�@�Q). ���|�Q���O�̂Ƃ��C�����Q
�@�@�@(6)����C�����Q���Q�{�Q�E�E�E(8)
�@�@�@���̂Ƃ��C�O�����|�Q��(���Q�|�S���Q���{�S)�P�^�Q����C
�@�@�@�@(���|�Q)�Q�����Q�|�S���Q���{�S
�@�@�@�@���S(���Q�|�P)�����O
�@�@�@�@�������O
�@�@�@�����(8)�ɔ�����D
�@�܂Ƃ߂�ƁC�O�������Q���Q�|�Q
�@i)�Cii)���C�O�������Q���Q�|�Q
�i�ʉ��j�i�O���t���g�킸�����Ȃ�ĐM�����Ȃ��D�O���t���g���ĊȒP�ɉ����ׂ��ł��j
�@��(��)�����Q�|�����{���Q���|�P�Ƃ���D
�@�Q����������(��)���O�̂Q�������C���Ƃ���ƁC���ƌW���̊W����C
�@�@���{�������C���������Q���|�P
i). �|�P�����������P�̂Ƃ��C�O���t����C
�@�@��(�|�P)���O�E�E�E(1)
�@�@��(�P)���O�E�E�E(2)
�@�@�|�P��(���{��)�^�Q���P�E�E�E(3)
�@�@��((���{��)�^�Q)���O�E�E�E(4)

�@(1)���C�P�|���{���Q���|�P��(���Q�|�P)�����O
�@�@�������O�E�E�E(1)'
�@(2)���C�P�{���{���Q���|�P��(�P�{���Q)�����O
�@�@�������O
�@(1)'�ƈ�v����D
�@(3)���C�|�P�����^�Q���P
�@�@���|�Q�������Q
�@(1)'���C�O�������Q�E�E�E(5)
�@ �@(4)���C��(���^�Q)�����Q�^�S�|���Q�^�Q�{���Q���|�P���O
�@�@�����Q�|�S���Q���{�S���O
�@�@�������Q���Q�|�Q�C�Q���Q�{�Q����
�@(5)���C�O�������Q���Q�|�Q�E�E�E(6)
ii). �����|�P�������P�C�܂��́C�|�P�������P�����̂Ƃ��C�O���t����C
�@�@��(�P)��(�|�P)���O
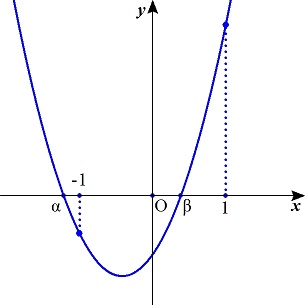
�@�@��(���Q�|�P)���E(�P�{���Q)�����O
�@�@���Q���O
�@�@�������O
�@i)�Cii)���C�O�������Q���Q�|�Q
���Q�i�`�}�`�}���͖̂ʓ|�D�v�Z�ŃS���S�����ׂ��ł��j
�@����cos���C����sin���Ƃ���ƁC
�@�@�����������}(�P�|���Q)�P�^�Q�}(�P�|���Q)�P�^�Q���O
�@�̂ɂ������O�ł���C
�@�@�����}(�P�|���Q)�P�^�Q���}(�P�|���Q)�P�^�Q
�@���ӂ��Q�悷��ƁC
�@�@���Q���Q�}�Q��(�P�|���Q)�P�^�Q���{(�P�|���Q)���P�|���Q
�@�@��(�P�{���Q)���Q�}�Q��(�P�|���Q)�P�^�Q���|���Q���O�E�E�E(1)
�@�P�{���Q���O�ł���̂ŁC����͂��̂Q���������ł���D
�@���ʎ����c�Ƃ���ƁC
�@�@�c�^�S�����Q(�P�|���Q)�{(�P�{���Q)���Q���Q���Q
�@(1)�������ƁC
�@�@����{�}��(�P�|���Q)�P�^�Q�}���Q�E��}�^(�P�{���Q)��{�}(�P�|���Q)�P�^�Q�}���Q}�E���^(�P�{���Q)
�@�|�P�������P�ŁC�|�P�������P�C�������O�̂Ƃ��ɓ_(���C����)���v���b�g���C���������̒l�͈̔͂����߂�D
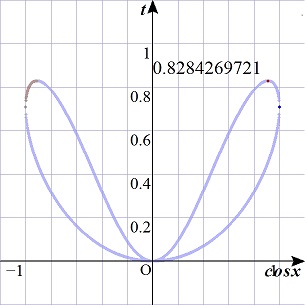
�@�O���t���C�O�������O.�W�Q�W�S�Q�V�i���Q���Q�|�Q�j�ł��邱�Ƃ�������D
�i�ʉ��j�i���w�̖��Ȃ̂�����C���P�̌��ʂ��g��Ȃ��̂͐M�����Ȃ��j
�@�@cos��sin�������E�E�E(1)
�@�@sin���{cos�������E�E�E(2)
�Ƃ���D
�@(1)���C
�@�@cos�Q��sin�Q�������Q
�@�@��(�P�|sin�Q��)(�P�|cos�Q��)�����Q
�@�@���P�|(sin�Q���{cos�Q��)�{sin�Q��cos�Q�������Q�E�E�E(1)'
�@(2)���C
�@�@sin�Q���{�Qsin��cos���{cos�Q�������Q�E�E�E(2)'
�@(1)'�{(2)'���C
�@�@�P�{sin�Q��cos�Q���{�Qsin��cos�����Q���Q
�@�@��(�P�{sin��cos��)�Q���Q���Q�E�E�E(3)
�@�|�P��sin�����P�C�|�P��cos�����P���C�|�P��sin��cos�����P
�@�@���P�{sin��cos�����O
�@�܂������O����C(3)���C
�@�@�P�{sin��cos�������Q��
�@�@��sin��cos�������Q���|�P�E�E�E(4)
�@(2)�C(4)����Csin���Ccos���́C���̂Q��������
�@�@���Q�|�����{(���Q���|�P)���O
�̂Q���ł���D
�@�|�P��sin�����P�C�|�P��cos�����P�C�����O�ł���̂ŁC���P�̌��ʂ���C
�@�@�O�������Q���Q�|�Q
�u�l�c�����v
10/05 09��46���@��M �X�V 10/27
���P
�i�ʉ����̂Q�j
�i�Ƃ��Ƃ�O���t���g���̂����ŁC�Q�����̖��́C�Q���������̉��ƌW���̊W���g���ĉ����̂��D���ł��D���������̖��ł́u���Ȃ��Ƃ��P�̉��v�ƂȂ��Ă���C�����|�P�������P�܂��́|�P�������P�����̏ꍇ�́C�ǂ����Ă��O���t���g�킴��Ȃ��̂ŁC������߂Ă��܂����j
�@�Q�����������Q�|�����{��Q���|�P���O�̂Q�������C���Ƃ���D
�@�|�P�����������P�܂��́|�P�����������P�̏ꍇ�݂̂��l����D
�@�����������̂ŁC���ʎ����c�Ƃ���ƁC
�@�@�c�����Q�|�S(��Q���|�P)�����Q�|�S��Q���{�S���O
�@�@�������Q��Q�|�Q�C�Q��Q�{�Q�����E�E�E(1)
�@���ƌW���̊W����C
�@�@���{�������C��������Q���|�P�E�E�E(2)
�@�|�P�������P�C�|�P�������P���C
i). �����P�������P
ii). �����|�P�������|�P
�@i)�̂Ƃ��C���|�P���O�����|�P���O
�@����́C���Ɠ��l�ł���D
�@�@(���|�P)�{(���|�P)���O����(���|�P)(���|�P)���O
�@�@�����{�����Q�E�E�E(3)�@���@�����|(���{��)�{�P���O�E�E�E(4)
�@(2)�C(3)���C�����Q
�@(1)���C�����Q��Q�|�Q�E�E�E(5)
�@(2)�C(4)���C(��Q���|�P)�|���{�P���O
�@�@��(��Q�|�P)�����O
�@�@�������O
�@(5)���C�O�������Q��Q�|�Q�E�E�E(6)
�@ii)�̂Ƃ��C���{�P���O�����{�P���O
�@����́C���Ɠ��l�ł���D
�@�@(���{�P)�{(���{�P)���O����(���{�P)(���{�P)���O
�@�@�����{�����|�Q�E�E�E(7)�@���@�����{(���{��)�{�P���O�E�E�E(8)
�@(2)�C(7)���C�����|�Q
�@�����(6)�����D
�@(2)�C(8)���C(��Q���|�P)�{���{�P���O
�@�@��(��Q�{�P)�����O
�@�@�������O
�@�����(6)�����D
�@�܂Ƃ߂�ƁC
�@�@�O�������Q��Q�|�Q
�u�l�c�����v
10/07 09��56���@��M �X�V 10/27
���P
�i�ʉ����̂R�j�i���n�͂���ς���ςʼn����Ȃ���I�j
�@���Q�|�����{��Q���|�P���O�i�|�P�������P�j����C
�@�@��(���|��Q)�����Q�|�P
�@������Q����C
�@�@����(���Q�|�P)�^(���|��Q)
�@�@�������^������{�Q���E(���|��Q)�|(���Q�|�P)�E�P}�^(���|��Q)�Q
�@�@�@�@�@�@�@�@��(���Q�|�Q��Q�E���{�P)�^(���|��Q)�Q
�@�����^�������O�C�|�P�������P����C������Q�|�P
�@�|�P��������Q�|�P�̂Ƃ��C�����^�������O
�@��Q�|�P�������P�̂Ƃ��C�����^�������O
�@�̂ɂ��́C������Q�|�P�̂Ƃ��C�ő�l
�@�@����{(��Q�|�P)�Q�|�P}�^{(��Q�|�P)�|��Q}���Q��Q�|�Q
���Ƃ�D
�@�܂��C�����}�P�̂Ƃ��C�����O
�@�܂Ƃ߂�ƁC�O�������Q��Q�|�Q
�i�ʉ����̂S�j�i����搶�̃A�h�o�C�X���j
�@�^���������C���Q�|�P����(���|��Q)�ƕό`����D
�@�̂ɋȐ��������Q�|�P�i�|�P�������P�j�̃O���t�ƁC����������(���|��Q)�̃O���t�����L�_�����Ƃ��̂��̒l�͈̔͂����߂�悢�D
i). �����O�̂Ƃ��C���L�_�����݂���D
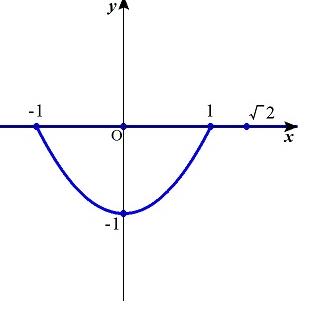
ii). �^�Q���������́C�����Q��Q�}�Q�̂Ƃ��C�d�������D
�@�����Q��Q�|�Q�̂Ƃ��C���L�_�����݂���D
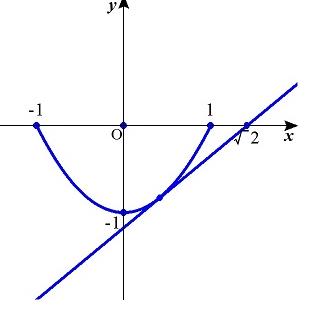
iii). �O�������Q��Q�|�Q�̂Ƃ��C���L�_�����݂��C���̏ꍇ�ɂ́C���L�_�͑��݂��Ȃ��D
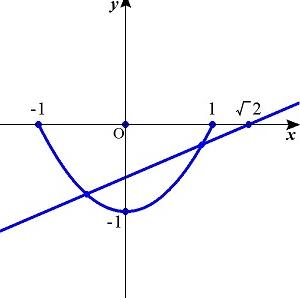
�@�ȏ���C���̒l�͈̔͂́C�O�������Q��Q�|�Q
�u�l�c�����v
10/07 11��50���@��M �X�V 10/27
���P
�i�ʉ����̂T�j�i�u���Ȃ��Ƃ��v������C��邱�Ƃ͂ЂƂD�r�����ہj
�@�r�����ۂ��l����D���������C���������C����炪��������|�P�����C�܂��͂P����ł���Ɖ��肷��D
�@���ʎ����c�Ƃ���ƁC
�@�@�c�����Q�|�S(��Q���|�P)���O
�@�@�������Q��Q�|�Q�C�Q��Q�{�Q�����E�E�E(1)
�@�܂����ƌW���̊W���C���{�������C��������Q���|�P�E�E�E(2)
i). �����P�C�����P�̂Ƃ��C
�@�@���|�P���O�C���|�P���O
�@�@��(���|�P)�{(���|�P)���O�C(���|�P)(���|�P)���O
�@�@�����{�����Q�E�E�E(3)�@�����|(���{��)�{�P���O�E�E�E(4)
�@(2)�C(3)���C�����Q
�@(1)���C�����Q��Q�{�Q�E�E�E(5)
�@(2)�C(4)���C(��Q���|�P)�|���{�P���O
�@�@��(��Q�|�P)�����O
�@�@�������O
�@�����(5)�����D
ii). �����|�P�C�����|�P�̂Ƃ��C
�@�@���{�P���O�C���{�P���O
�@�@��(���{�P)�{(���{�P)���O�C(���{�P)(���{�P)���O
�@�@�����{�����|�Q�E�E�E(6)�@�����{(���{��)�{�P���O�E�E�E(7)
�@(2)�C(6)���C�����|�Q
�@(1)���C�����|�Q�E�E�E(8)
�@(2)�C(7)���C(��Q���|�P)�{���{�P���O
�@�@��(��Q�{�P)�����O
�@�@�������O
�@�����(8)�ɔ�����D
iii). �����|�P�C�����P�̂Ƃ��C��(��)�����Q�|�����{��Q���|�P�Ƃ���ƁC
�@�@��(�P)���O�C��(�|�P)���O
�ƂȂ�悢�D
�@�@��(�P)���P�|���{��Q���|�P��(��Q�|�P)�����O
�@�@�������O
�@(1)���C�����O�E�E�E(9)
�@�܂��C
�@�@��(�|�P)���P�{���{��Q���|�P��(��Q�{�P)�����O
�@�@�������O
�@�����(9)�ƈ�v����D
�@�ȏ���܂Ƃ߂�ƁC
�@�@�����O�@�܂��́@�Q��Q�{�Q����
�@(1)���C���߂�͈͂́C
�@�@�O�������Q��Q�|�Q
NO3�u���N���̂�������v 10/07 17��13���@��M �X�V 10/27
���1
![]()
���ӂ�y�Ƃ����܂��B
![]()
![]()
����2�����̒��_�́A![]()
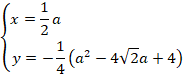
���A![]() �����̎��ɓ����ƁA
�����̎��ɓ����ƁA
![]()
���_�́A���̏�ɓʂ̐Ԃ��O���t��ɂ���܂��B
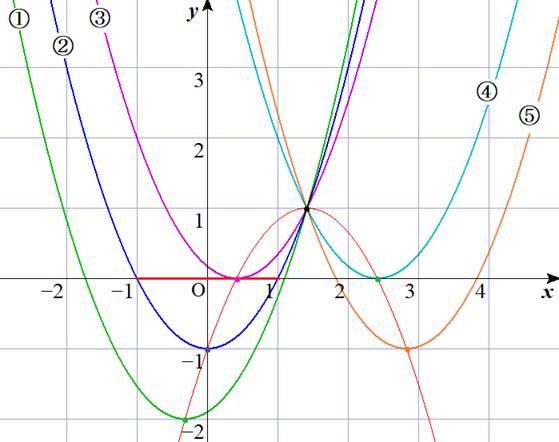
�Ԃ̃O���t��ɒ��_�����O���t�����������ׂ܂��B
���ɒ��_���A�@��![]() �A�A��
�A�A��![]() �A�B��
�A�B��![]() �A�C��
�A�C��![]() �A�D��
�A�D��![]() �Ƃ��܂��B
�Ƃ��܂��B
���ɁA�@�� ![]() �A�A��
�A�A�� ![]() �A�B��
�A�B�� ![]() �A�C��
�A�C�� ![]() �A�D��
�A�D�� ![]() �ł��B
�ł��B
���́A
![]()
![]()
![]()
![]()
![]()
���̂Q�����́A
![]()
![]() �Ƃ���ƁAa�̒l�ɂ�炸�A
�Ƃ���ƁAa�̒l�ɂ�炸�A
![]()
�ł��̎����������܂��B�ia�ɂ��Ă̍P�����ł��j
�i�@ ��D�̂��ׂăO���t���A�_
![]() ��ʂ�܂��j
��ʂ�܂��j
![]() �͈̔͂̉����l����ƁA
�͈̔͂̉����l����ƁA
�@�͂���܂���B�i�͈͂ɏ������Ȃ���A2�̎������ł��j
�A�� ![]() �����ł��B
�����ł��B
�B�́A![]() �����ł��B(�d��)
�����ł��B(�d��)
�C�́A����܂���B�i�͈͂ɏ������Ȃ���A�d���ł��j
�D�́A����܂���B�i�͈͂ɏ������Ȃ���A2�̉��ł��j
�ȏォ��A![]() �����ƂȂ�܂��B
�����ƂȂ�܂��B
���2
![]()
����x���^����ꂽ�Ƃ��A�ǂ��y�ł��̎����������邩���l���܂��B
![]() ����̎��ɑ�����܂��B
����̎��ɑ�����܂��B
![]()
![]()
![]() �Ő�������2���������������܂��B
�Ő�������2���������������܂��B
![]()
![]()
�����̒��́A
![]()
![]()
����āA
![]()
��
![]()
![]()
�����ŁA![]() �́A���Ȃ̂ŕ����̂Ƃ���́A���̂��̂�p���܂��B
�́A���Ȃ̂ŕ����̂Ƃ���́A���̂��̂�p���܂��B
��
![]()
1������ [0, 2��) �ŁAt�̑����ׂ܂��B
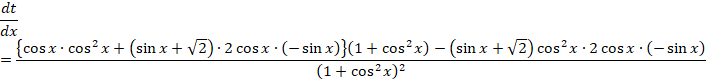
���q�́A
![]()
![]()
![]()
![]()
![]()
�����ŁA�����藝����p���ĕ�������ƁA
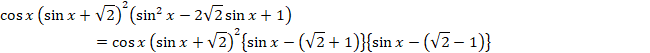
��
![]()
��̎��ŁA�����̕����͐��A���F�̕����͕��ł��B
![]() ���A
���A![]()
![]() �̉������A���Ƃ��܂��B
�̉������A���Ƃ��܂��B

|
x |
0 |
��� |
�� |
��� |
��/2 |
��� |
�� |
��� |
3��/2 |
��� |
2�� |
|
dt/dx |
�{ |
�{ |
0 |
�| |
0 |
�{ |
0 |
�| |
0 |
�{ |
|
|
t |
|
↗���� |
A |
↘���� |
B |
↗���� |
C |
↘���� |
D |
↗���� |
|
A�AB�AC�AD�̋ɒl�ׂ܂��B
![]()
�EA�AC�ɂ��ẮA![]() ���A
���A
![]()
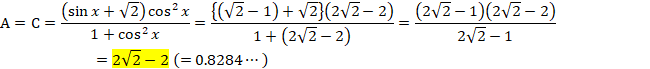
�EB�AD�ɂ��ẮA![]() ���A
���A
![]()
����āA![]()
NO4�u��x�Ђ����v 10/13 10��51���@��M
�X�V 10/27
[���1]
x^2-a*x+(��2)*a-1=0
��
x^2-1=a*(x-��2).
������ y=x^2-1 ��
��_ (��2,0) ��ʂ钼�� y=a*(x-��2) ���C
���Ȃ��Ƃ� 1 �̌�_�������C���̌�_��x���W��
-1 �ȏ� ���� 1 �ȉ� �ƂȂ�悤�� a �̒l�͈̔͂����߂�悢�D
0��a��2*(��2 - 1) (��)
[���2]
t=cos(x)*sin(y)��0 ---(1)
t=sin(x)+cos(y)��0 ---(2)
(1)�̗��ӂ��悵�āC
t^2=((cos(x))^2)*((sin(y))^2)�D
����āC
t^2=(1-(sin(x))^2)*(1-(cos(y))^2)
---(3)
(2)���C
cos(y)=t-sin(x)�D
�����(3)���C
t^2=(1-(sin(x))^2)*(1-(t-sin(x))^2)�D
sin(x)=u �Ƃ����ēW�J���Đ�������ƁC
(u^2-1-(u-��2)*t)*(1-u^2+(u+��2)*t)=0�D
����āC
u^2-1-(u-��2)*t=0 ---(4)
(�����ŁC1-u^2+(u+��2)*t=0�ƂȂ邱�Ƃ͖����D
�Ȃ��Ȃ�C-1��u��1�Ct��0 ���C 1-u^2+(u+��2)*t��0 )
u�ɂ��Ă̓�����(4)���C-1��u��1�͈̔͂ɏ��Ȃ��Ƃ�
��̉������悤��
t�̒l�͈̔͂́C��̖��ɂ��C
0��t��2*(��2 - 1)�D
����� t��0 �Ƃ���C
0��t��2*(��2 - 1) ---(5)
�ȏ���C(1)�C(2)�������ɐ��藧�Ƃ���Ƃ��C
(5)�����藧���Ƃ��킩�����D
���ɁC(5)�����藧�Ƃ��C(1)�C(2)���ɐ��藧������悤��
cos(x)�Csin(y)�Csin(x)�Ccos(y) �����݂��邱�Ƃ������D
t���C0��t��2*(��2 - 1)�����悤�ȔC�ӂ̎����Ƃ���D
u�ɂ��Ă̓�����(4)�� -1��u��1 �͈̔͂ɏ��Ȃ��Ƃ�
1�̉������D�����̉��̂����C�傫���Ȃ����̉���
u=�� �Ƃ���D
��^2-1-(��-��2)*t=0 ���C
t=(1-��^2)/(��2-��)�D
sin(x)=�� ���� -��/2��x����/2 �ƂȂ�悤�� x ���Ƃ邱�Ƃ��ł���D
���̂Ƃ��Ccos(x)=��(1-��^2)�D
�܂��C-1��t-����1 �ł���D�@
(�Ȃ��Ȃ�C1-(t-��)^2=1-((1-��^2)/(��2-��)-��)^2=(1-��^2)/(��2-��)^2 �� 0)
����āCcos(y)=t-��
���� 0��y���� �ƂȂ�悤�� y ���Ƃ邱�Ƃ��ł���D
���̂Ƃ��Csin(y)=��(1-(t-��)^2)=(��(1-��^2))/(��2-��)�D
sin(x)+cos(y)=��+(t-��)=t �ł��邩��C(2)�����Ă���D
����ɁC
cos(x)*sin(y)
=(��(1-��^2))*(��(1-��^2))/(��2-��)
=(1-��^2)/(��2-��)
=t
�ł��邩��C(1)���������Ă���D
�ȏ���Ct�̂Ƃ肤��l�͈̔͂́C0��t��2*(��2 - 1) �ł����
���_�ł���D
(�ȏ�)
NO5�u�W���[�J�[�v �@
10/13 22��49���@��M �X�V 10/27


���2���������Ƃ��C���1�Ɠ�����������A�s�v�c�ł����B
�ꌩ�A���Ă������ʖ��Ȃ̂ɁA
�������ɂ���ē������ɋA���ł���Ƃ́B
�����Əo��҂̈Ӑ}�Ȃ̂��ȂƎv���܂����B
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
