—كکaŒ³”N11Œژ24“ْ
 [—¬‚êگ¯]
[—¬‚êگ¯]
پ@پ@پ@پ@‘و379‰ٌگ”ٹw“I‚ب‰•ه‰ً“ڑ
پ@پ@پ@پ@پƒ‰ً“ڑ•هڈWٹْٹشپF10Œژ27“ْپ`11Œژ24“ْپ„
پm‘fگ”‚جکaپn
پ@
پ@ڈ‰‚ك‚ج‚ژŒآ‚ج‘fگ”‚جکa‚ًS‚ژ‚ئ‚¨‚پB
—ل‚¦‚خپAS‚Pپپ‚QپAS2=‚Qپ{‚Rپپ‚TپAS‚Rپپ‚Qپ{‚Rپ{‚Tپپ10پ@‚إ‚ ‚éپB
”Cˆس‚جژ©‘Rگ”‚ژ‚ة‘خ‚µ‚ؤپAS‚ژ‚ئSn+1‚جٹش‚ة•½•ûگ”‚ھ‘¶چف‚·‚邱‚ئ‚ًڈط–¾‚¹‚وپB
پ@‘fگ”—ٌ‚حپA‚QپA‚RپA‚TپA‚VپA11پA13پA17پAپEپEپE‚ة‚آ‚¢‚ؤپA‚»‚ج‚ژ”ش–ع‚جگ”‚ھ‚ژ‚ج‚ا‚¤‚¢‚¤ٹضگ”‚ئ‚ب‚é‚©•ھ‚©‚ء‚ؤ‚¢‚ـ‚¹‚ٌپBڈم‚ج–â‘è‚ًڈط–¾‚·‚邱‚ئ‚حچ¢“ï‚ة‚ب‚è‚ـ‚·پB
پ@
‚»‚±‚إپAپuˆê”ت‰»پv‚µ‚½ژں‚ج–â‘è‚ًڈط–¾‚µ‚ؤ‚‚¾‚³‚¢پB
–â‘èپ@ژ©‘Rگ”—ٌ{a‚ژ}‚حژں‚جڈًŒڈ‚ً‚ف‚½‚µ‚ؤ‚¢‚éپB
پ@a‚Pپپ‚QپAa‚Qپپ‚RپAa‚ژپ{‚Pپ\a‚ژپ†‚Qپi‚ژپ†‚Qپj
S‚ژپپa‚Pپ{a‚Qپ{پEپEپEپ{a‚ژپ@
‚ئ‚¨‚‚ئ‚«پA”Cˆس‚جژ©‘Rگ”‚ژ‚ة‘خ‚µ‚ؤپAS‚ژ‚ئSn+1‚جٹش‚ة•½•ûگ”‚ھ‘¶چف‚·‚邱‚ئ‚ًڈط–¾‚¹‚وپB
ƒqƒ“ƒgپF”w—–@‚ً—ک—p‚µ‚ؤ‚‚¾‚³‚¢پB
پƒڈo“TپFپuگ”ٹw“Iژvچl‚جچ\‘¢پv’ثŒ´گ¬•vپ@’کپ@پiŒ»‘مگ”ٹwژذپjپ„
NO1پuƒXƒ‚پ[ƒNƒ}ƒ“پv 10/29
23ژ47•ھپ@ژَگM چXگV 11/24
‰ٌ“ڑ
S(n)=2+3+a(3)+a(4)+...+a(n)
>1+3+5+7+...
=n^2
S(n+1)>(n+1)^2
so...
n^2+1<=S(n)
(n+1)^2+1<S(n+1)
so...
S(n)‚ئS(n+1)‚ئ‚جٹش‚ة‚حپA(n+1)^2‚ئ‚¢‚¤•½•ûگ”‚ھ‘¶چف‚µ‚ؤ‚é
QED
ˆê”ت‰»‚µ‚ؤچl‚¦‚邱‚ئ‚ھƒuƒŒپ[ƒNƒXƒ‹پ[‚ة‚ب‚é‚ئ‚¢‚¤‚ج‚ھ–ت”’‚¢‚إ‚·‚ث ^^پ™
پƒگ…‚ج—¬‚êپF‚r‚ژپپ‚Qپ{‚Rپ{‚پ‚Rپ{‚پ‚Sپ{‚پ‚Tپ{پEپEپEپ{‚پ‚ژ
پ@پ@پ@پ@پ„‚Pپ{‚Rپ{‚Tپ{‚Vپ{‚Xپ{پEپEپEپ{(‚Q‚ژپ|‚P)
پ@پ@پ@پ@پپ‚ژ‚Q
پ@پ@پˆ‚ژ‚Qپƒ‚r‚ژپC(‚ژپ{‚P)‚Qپƒ‚r‚ژپ{‚P
پ@‚µ‚©‚µ‚¾‚©‚ç‚ئ‚¢‚ء‚ؤپC
پ@پ@‚ژ‚Qپƒ‚r‚ژپ…(‚ژپ{‚P)‚Qپƒ‚r‚ژپ{‚P
‚ئ‚ب‚é‚©‚ا‚¤‚©‚ح•ھ‚©‚ç‚ب‚¢پD
پ@پ@‚ژ‚Qپƒ(‚ژپ{‚P)‚Qپƒ‚r‚ژپƒ‚r‚ژپ{‚P
‚©‚à’m‚ê‚ب‚¢پD
پuƒXƒ‚پ[ƒNƒ}ƒ“پv 11/14 20ژ35•ھپ@ژَگM
چXگV 11/24
‚ب‚é‚ظ‚ا...!!
so... ‚à‚¤ˆê“xچl‚¦‚ؤ‚ف‚ـ‚µ‚½...
‚ژ‚Qپƒ(‚ژپ{‚P)‚Qپƒ‚r‚ژپƒ‚r‚ژپ{‚P
‚ئ‚·‚é‚ئپA
S(n+1)‚ح(n+2)^2-1‚ـ‚إ‚ئ‚ب‚è‚ـ‚·‚ھپA
S(n+1)=(n+2)^2-1 or (n+2)^2-2‚ب‚çپAS(n+2)>(n+2)^2+0 or +1 ‚ب‚ج‚إپAS(n+1)‚ئS(n+2)‚جٹش‚ة‚ح(n+2)^2‚ئ‚¢‚¤•½•ûگ”‚ھ‚ ‚èپA
S(n+1)=(n+2)^2-3 or (n+2)^2-4 ‚ب‚çپAS(n+3)>(n+2)^2+0 or +1 ‚ب‚ج‚إپAS(n+1)‚ئS(n+2)‚جٹش‚ة(n+2)^2
ˆب‰؛پA‘½•ھپA“¯—l‚ةŒ¾‚¦‚邱‚ئ‚ئ‚ب‚èپA
ژہچغ‚ةپA 2,3,5,7‚إپA2^2<3^2<S(3)<S(4)‚ً–‚½‚µ‚ؤ‚¢‚é‚ج‚إŒ¾‚¦‚éپB
Œ‹‹اپA
(1) ‚ژ‚Qپƒ‚r‚ژپ…(‚ژپ{‚P)‚Qپƒ‚r‚ژپ{‚P ‚ج‚ئ‚«‚ح–¾‚ç‚©پB
(1) ‚ژ‚Qپƒ(‚ژپ{‚P)‚Qپƒ‚r‚ژپƒ‚r‚ژپ{‚P ‚ج‚ئ‚«‚حپAڈم‚جƒAƒvƒچپ[ƒ`‚إ...
‚ئ‚¢‚¤‚±‚ئ‚إ‚ح‚¢‚©‚ھ‚إ‚µ‚ه‚¤‚©پH
NO2پu‘پ‹N‚«‚ج‚¨‚¶‚³‚ٌپv 11/01 17ژ34•ھپ@ژَگM چXگV 11/24
![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
![]()
‚و‚ء‚ؤ ![]()
‚ن‚¦‚ة ![]() ‚ئ‚ب‚è‚ـ‚·پB
‚ئ‚ب‚è‚ـ‚·پB
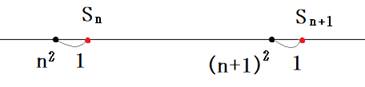
‘و2چ€ˆبچ~‚ھ“™چ·2‚جگ”—ٌپiٹïگ”پj‚حپASn‚ئSn+1 ‚جٹش‚ة•½•ûگ”(n+1)2 پiچ€گ”‚ج•½•ûپj‚ھ‚ ‚è‚ـ‚·پB
–â‘è‚جڈًŒڈ‚حپA![]() ‚ب‚ج‚إپA“–‘RSn‚ح‘و2چ€ˆبچ~‚ھٹïگ”‚جڈêچ‡‚و‚è‘ه‚«‚‚ب‚è‚ـ‚·پB
‚ب‚ج‚إپA“–‘RSn‚ح‘و2چ€ˆبچ~‚ھٹïگ”‚جڈêچ‡‚و‚è‘ه‚«‚‚ب‚è‚ـ‚·پB
‚¾‚©‚çپASn‚ئSnپ{1‚جٹش‚ة•½•ûگ”‚ھ‘¶چف‚·‚é‚ج‚ح“–‚½‚è‘O‚جٹ´‚¶‚ھ‚µ‚ـ‚·پB
—ل‚¦‚ؤ‚¢‚¤‚ئپu•à‚¢‚ؤ‚ا‚جڈلٹQ‚à‰z‚¦‚ç‚ê‚é‚ئ‚«پA‘–‚ء‚ؤ‚à‚·‚ׂؤ‚جڈلٹQ‚ً‰z‚¦‚ç‚ê‚邱‚ئ‚ًژ¦‚¹پv‚ئ‚¢‚¤ٹ´‚¶‚إ‚·پB
‘–‚é‚ئ‚«‚ح•à‚‚ئ‚«‚و‚è‚و‚è•à•‚ھچL‚‚ب‚é‚ج‚إ‚·‚©‚çپB
پuٹ´‚¶پv‚ھچ‡‚ء‚ؤ‚¢‚é‚©ٹm‚©‚ك‚ـ‚·پB
Sn+1‚ھ(nپ{k)2 ‚ً’´‚¦‚éڈêچ‡‚ًچl‚¦‚ـ‚·پB(nپ†2پAkپ†1)
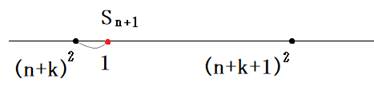
![]() ‚ةپA
‚ةپA![]() ‚ً‰ء‚¦‚é‚ئپA
‚ً‰ء‚¦‚é‚ئپA![]() ‚ئ‚ب‚è‚ـ‚·پB
‚ئ‚ب‚è‚ـ‚·پB
‚±‚ج’l‚حپA(nپ{k)2 ‚جژں‚ج•½•ûگ”‚و‚è1‘ه‚«‚‚ب‚è‚ـ‚·پB
![]()
‘وnچ€‚ـ‚إ‚حپA![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
‚»‚µ‚ؤپA
![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
‚·‚é‚ئپA
![]()
‚³‚ؤپAچإڈ¬‚جSn+2‚ًچl‚¦‚ـ‚·پB
![]() ‚ئ‚µ‚ـ‚·پB
‚ئ‚µ‚ـ‚·پB
‚±‚ج’l‚ئپAگو‚ظ‚ا‚ج’l‚ً”ن‚ׂـ‚·پB
![]()
‚ب‚ج‚إپAk‚ھ1‚و‚è‘ه‚«‚¢‚ئ‚«‚حپA![]() ‚ج•û‚ھ‘ه‚«‚¢‚ج‚إپASn+2 ‚ھ•½•ûگ”‚ً’´‚¦‚é‚ج‚ح–¾‚ç‚©‚إ‚·پB
‚ج•û‚ھ‘ه‚«‚¢‚ج‚إپASn+2 ‚ھ•½•ûگ”‚ً’´‚¦‚é‚ج‚ح–¾‚ç‚©‚إ‚·پB
ژہچغپA
![]()
![]()
![]()
![]()
‚ئ‚ب‚è‚ـ‚·پB
![]()
![]()
‚±‚ج’l‚حپAkپ†2‚ج‚ئ‚«پAگ³‚ئ‚ب‚è‚ـ‚·پB
‚آ‚ـ‚èپAkپ†2‚ج‚ئ‚«پASnپ{1‚ئSnپ{2‚جٹش‚ة ![]() Œآ‚ج•½•ûگ”‚ھ‘¶چف‚µ‚ـ‚·پB
Œآ‚ج•½•ûگ”‚ھ‘¶چف‚µ‚ـ‚·پB
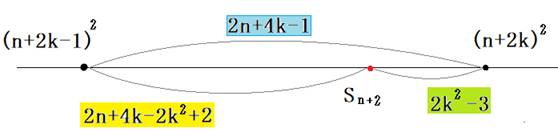
S1,S2,S3,¥¥¥,Sn‚ج‚ا‚±‚©—ׂèچ‡‚¤“ٌگ”‚جٹش‚ة2Œآˆبڈم‚ج•½•ûگ”‚ھ‚ ‚ء‚½‚ئ‚µ‚ـ‚·پB
‚·‚é‚ئپASn‚ً’´‚¦‚ب‚¢چإ‘ه‚ج•½•ûگ”‚حپA(nپ{1)2ˆبڈم‚ة‚ب‚è‚ـ‚·پB
‚و‚ء‚ؤپAanپ{1‚حپA2(nپ{1)پ{1‚و‚è‘ه‚«‚‚ب‚é‚ج‚إپASnپ{1‚حپAڈ‚ب‚‚ئ‚à (nپ{2)2 ‚ً’´‚¦‚ـ‚·پB
چ،‰ٌ‚حپAڈo‘è‚جˆسگ}‚ھ‚و‚•ھ‚©‚è‚ـ‚¹‚ٌ‚إ‚µ‚½پB
”w—–@‚ًژg‚¤‚ئ‚ ‚è‚ـ‚·‚ھپAƒqƒ“ƒg‚à‚و‚—‰ً‚إ‚«‚ـ‚¹‚ٌ‚إ‚µ‚½پB
NO3پu“ٌ“x’ذ‚¯”’چطپv 11/04
15ژ09•ھپ@ژَگM چXگV 11/24
(ڈط–¾)
nپ†2‚ب‚é”Cˆس‚جژ©‘Rگ” n ‚ة‘خ‚µ‚ؤپC
a[n]
=(a[n]-a[n-1])+(a[n-1]-a[n-2])+پc+(a[3]-a[2])+(a[2]-a[1])+a[1]
پ†2*(n-2)+(3-2)+2
=2*n-1پD
‚آ‚ـ‚èپCa[n]پ†2*n-1 (nپ†2) ‚إ‚ ‚éپD
‚و‚ء‚ؤپC
S[n+1]
=a[1]+ƒ°[j=2پ`n+1]a[j]
=2+ƒ°[j=2پ`n+1]a[j]
پ†2+ƒ°[j=2پ`n+1](2*j-1)
=1+(n+1)^2پD
‚آ‚ـ‚èپC1+(n+1)^2پ…S[n+1]پ@(nپ†1) ---(1)
‚ھگ¬‚è—§‚ء‚ؤ‚¢‚éپD
‚ـ‚½پC2پ…jپ…n ‚ب‚é”Cˆس‚جژ©‘Rگ” jپCn ‚ة‘خ‚µ‚ؤپC
a[n+1]
=(a[n+1]-a[n])+(a[n]-a[n-1])+پc+(a[j+1]-a[j])+a[j]
پ†2*(n-j+1)+a[j]پD
‚و‚ء‚ؤپC
a[j]پ…a[n+1]-2*(n-j+1) (2پ…jپ…n) ---(2)
‚ھگ¬‚è—§‚ء‚ؤ‚¢‚éپD
2=S[1]پƒ4پƒS[2]=5 ‚إ‚ ‚é‚©‚çپCS[1] ‚ئ S[2] ‚جٹش‚ة‚ح
ٹm‚©‚ة•½•ûگ”‚ھ‘¶چف‚·‚éپD
‚¢‚ـپC2ˆبڈم‚ج‚ ‚éژ©‘Rگ” N ‚ة‘خ‚µ‚ؤپCS[N] ‚ئ S[N+1] ‚جٹش‚ة•½•ûگ”‚ھ
‘¶چف‚µ‚ب‚©‚ء‚½‚ئ‰¼’è‚·‚éپD
‚±‚ج‚ئ‚«پC
K^2پ…S[N]پƒS[N+1]پ…(K+1)^2 ---(3)
‚ب‚éژ©‘Rگ” K ‚ھ‘¶چف‚·‚éپD
(1),(3)‚و‚èپC1+(N+1)^2پ…(K+1)^2 ‚إ‚ ‚é‚©‚çپC Kپ†N+1 ---(4)
(3)‚و‚èپC S[N+1]-S[N]پ…(K+1)^2 - K^2پD
‚و‚ء‚ؤپCa[N+1]پ…2*K+1پD
‚±‚ê‚ئ(2)‚ئ‚©‚çپC
a[j]پ…2*(K-N+j)-1 (2پ…jپ…N)
‚إ‚ ‚éپD
‚و‚ء‚ؤپC
S[N]
=a[1]+a[2]+پc+a[N]
=2+ƒ°[j=2پ`N]a[j]
پ…2+ƒ°[j=2پ`N](2*(K-N+j)-1)
=K^2+2-(K-N+1)^2
پ…K^2+2-2^2 (پو (4)‚و‚è K-N+1پ†2)
=K^2-2
پƒK^2پD
‚آ‚ـ‚èپCS[N]پƒK^2 ‚ئ‚ب‚é‚ھپC‚±‚ê‚ح(3)‚ة”½‚·‚éپD
‚و‚ء‚ؤ–µڈ‚‚ھگ¶‚¶‚½پD
‚و‚ء‚ؤپC2ˆبڈم‚ج”Cˆس‚جژ©‘Rگ” n ‚ة‘خ‚µ‚ؤپCS[n] ‚ئ S[n+1] ‚جٹش‚ة•½•ûگ”‚ھ
‘¶چف‚·‚éپD
ˆبڈم‚و‚èپC”Cˆس‚جژ©‘Rگ” n ‚ة‘خ‚µ‚ؤپCS[n] ‚ئ S[n+1] ‚جٹش‚ة•½•ûگ”‚ھ
‘¶چف‚·‚邱‚ئ‚ھژ¦‚¹‚½پDپ@(ڈط–¾ڈI)
(ˆبڈم)
NO4پu•l“c–¾–¤پv
11/09 10ژ44•ھپ@ژَگM چXگV 11/24
‚پ‚Pپپ‚QپC‚پ‚Qپپ‚RپC‚پ‚ژپ{‚Pپ|‚پ‚ژپ†‚Qپi‚ژپپ‚QپC‚RپC‚SپCپEپEپEپjپC‚r‚ژپپƒ°‚Pپ…‚‹پ…‚ژپ@‚پ‚‹
پ@”w—–@‚إڈط–¾‚·‚éپD
پ@‚ ‚éگ³گ®گ”‚ژ‚ة‚¨‚¢‚ؤپC‚چ‚Qپ…‚r‚ژپƒ‚r‚ژپ{‚Pپ…(‚چپ{‚P)‚Q‚ئ‚ب‚éگ®گ”‚چ‚ھ‘¶چف‚·‚é‚ئ‰¼’è‚·‚é‚ئپC
پ@پ@‚r‚ژپ{‚Pپ…(‚چپ{‚P)‚Q
پ@پ@پ|‚r‚ژپ…پ|‚چ‚Q
پ@•سپX‚ً‰ء‚¦‚é‚ئپC
پ@پ@‚پ‚ژپ{‚Pپپ‚r‚ژپ{‚Pپ|‚r‚ژپ…(‚چپ{‚P)‚Qپ|‚چ‚Qپپ‚Q‚چپ{‚P
پ@پ@پˆ‚پ‚ژپ{‚Pپ…‚Q‚چپ{‚P
پ@‚پ‚ژپ{‚Pپ|‚پ‚ژپ†‚Q‚و‚èپC
پ@پ@‚پ‚ژپ…‚پ‚ژپ{‚Pپ|‚Qپ…‚Q‚چپ|‚P
پ@پ@پˆ‚پ‚ژپ|‚Pپ…‚پ‚ژپ|‚Qپ…‚Q‚چپ|‚Pپ|‚Q
پ@پ@پˆ‚پ‚ژپ|‚Qپ…‚پ‚ژپ|‚Pپ|‚Qپ…‚Q‚چپ|‚Pپ|‚QپE‚Q
پ@پ@پ@پEپEپE
پ@پ@پˆ‚پ‚ژپ|(‚ژپ|‚R)پ…‚Q‚چپ|‚Pپ|‚Q(‚ژپ|‚R)پپ‚Q(‚چپ|‚ژ)پ{‚TپEپEپE‡@
پ@پ@پˆ‚پ‚ژپ|(‚ژپ|‚Q)پ…‚Q‚چپ|‚Pپ|‚Q(‚ژپ|‚Q)پپ‚Q(‚چپ|‚ژ)پ{‚RپEپEپE‡A
پ@‡A‚و‚èپC‚پ‚Qپپ‚Rپ…‚Q(‚چپ|‚ژ)پ{‚R
پ@پ@پˆ‚چپ†‚ژ
i). ‚چپپ‚ژ‚ج‚ئ‚«پC‡@‚و‚èپC
پ@پ@‚پ‚Rپ…‚T
پ@‚ـ‚½پC‚پ‚Rپ†‚پ‚Qپ{‚Qپپ‚T
پ@پ@پˆ‚پ‚Rپپ‚T
پ@“¯—l‚ةپC
پ@پ@‚پ‚Sپپ‚پ‚Rپ{‚Qپپ‚V
پ@پ@‚پ‚Tپپ‚پ‚Sپ{‚Qپپ‚X
پ@پ@پEپEپE
پ@پ@پˆ‚پ‚ژپپ‚Q‚ژپ|‚Pپi‚ژپ†‚Qپj
پ@‚پ‚Pپپ‚Pپ{‚P‚©‚çپC
پ@پ@‚r‚ژپ{‚Pپپ‚Pپ{ƒ°‚Pپ…‚‹پ…‚ژپ{‚P(‚Q‚‹پ|‚P)
پ@پ@پ@پ@پپ‚Pپ{‚QپE‚Pپ^‚QپE(‚ژپ{‚P)(‚ژپ{‚Q)پ|(‚ژپ{‚P)
پ@پ@پ@پ@پپ‚ژ‚Qپ{‚Q‚ژپ{‚Q
پ@پ@پ@پ@پ„(‚ژپ{‚P)‚Qپپ(‚چپ{‚P)‚Q
پ@پ@پˆ‚r‚ژپ{‚Pپ„(‚چپ{‚P)‚Q
پ@‚±‚ê‚حپC‚r‚ژپ{‚Pپ…(‚چپ{‚P)‚Q‚ة”½‚·‚éپD
ii). ‚چپ„‚ژ‚ج‚ئ‚«پC
پ@‚ژپپ‚P‚ج‚ئ‚«پC‚چ‚Qپ…‚r‚Pپƒ‚r‚Qپ…(‚چپ{‚P)‚QپC‚·‚ب‚ي‚؟پC
پ@پ@‚چ‚Qپ…‚QپC‚Tپ…(‚چپ{‚P)‚Q
‚ئ‚ب‚éگ®گ”‚چ‚ح‘¶چف‚µ‚ب‚¢پD
پ@‚ژپپ‚Q‚ج‚ئ‚«پC‚چ‚Qپ…‚r‚Qپƒ‚r‚Rپ…(‚چپ{‚P)‚QپC‚·‚ب‚ي‚؟پC
پ@پ@‚چ‚Qپ…‚TپC‚P‚Oپ…‚Tپ{‚پ‚Rپ…(‚چپ{‚P)‚Qپiپو‚پ‚Rپ†‚پ‚Qپ{‚Qپپ‚Tپj
‚ئ‚ب‚éگ®گ”‚چ‚ح‘¶چف‚µ‚ب‚¢پD
پ@ˆبڈم‚و‚èپC‚ژپ†‚R‚ئ‚ب‚éپD
پ@‚±‚ج‚ئ‚«پC
پ@پ@‚پ‚ژپ…‚Q‚چپ|‚P
پ@پ@‚پ‚ژپ|‚Pپ…‚Q‚چپ|‚R
پ@پ@‚پ‚ژپ|‚Qپ…‚Q‚چپ|‚T
پ@پ@پEپEپE
پ@پ@‚پ‚Rپ…‚Q(‚چپ|‚ژ)پ{‚T
پ@پ@‚پ‚Qپپ‚R
پ@پ@‚پ‚Pپپ‚Q
پ@•سپX‚ً‰ء‚¦‚é‚ئپC
پ@پ@‚r‚ژپپ‚پ‚Pپ{‚پ‚Qپ{‚پ‚Rپ{پEپEپEپ{‚پ‚ژ
پ@پ@پ@پ@پ…‚Qپ{‚Rپ{{‚Q(‚چپ|‚ژ)پ{‚T}پ{{‚Q(‚چپ|‚ژ)پ{‚V}پ{{‚Q(‚چپ|‚ژ)پ{‚X}پ{پEپEپEپ{(‚Q‚چپ|‚P)
پ@پ@پ@پ@پپ{‚Pپ{‚Rپ{‚Tپ{پEپEپEپ{(‚Q‚چپ|‚P)}پ{‚Pپ|[‚Tپ{‚Vپ{‚Xپ{پEپEپEپ{{‚Q(‚چپ|‚ژ)پ{‚R}]
پ@پ@پ@پ@پƒ‚Pپ{‚Rپ{‚Tپ{پEپEپEپ{(‚Q‚چپ|‚P)
پ@پ@پ@پ@پپƒ°‚Pپ…‚‹پ…‚چ(‚Q‚‹پ|‚P)
پ@پ@پ@پ@پپ‚QپE‚Pپ^‚QپE‚چ(‚چپ{‚P)پ|‚چ
پ@پ@پ@پ@پپ‚چ‚Q
پ@پ@پˆ‚r‚ژپƒ‚چ‚Q
پ@‚±‚ê‚حپC‚چ‚Qپ…‚r‚ژ‚ة”½‚·‚éپD
پ@ˆبڈم‚ة‚و‚èپC‚·‚ׂؤ‚جگ³گ®گ”‚ژ‚ة‚¨‚¢‚ؤپC‚r‚ژپƒ‚چ‚Qپƒ‚r‚ژپ{‚P‚ئ‚ب‚éگ®گ”‚چ‚ھ‘¶چف‚·‚éپD
پi‘ه•د‚بڈط–¾‚إ‚µ‚½پj
پƒگ…‚ج—¬‚êپFڈo“T‚ج‰ً“ڑپ@12Œژ2“ْپ@‹Lڈqپ„
”w—–@‚ة‚و‚茋ک_‚ً”غ’肵‚ـ‚·پB
‚ ‚éژ©‘Rگ”‚ژ‚ة‘خ‚µ‚ؤ“K“–‚بژ©‘Rگ”‚‹‚ئ‚جٹش‚ةˆب‰؛‚جٹضŒW‚ھگ¬—§‚·‚邱‚ئ‚ئ‚ب‚éپB
پ@پ@پ@پ@‚‹‚Qپ…S‚ژپƒ‚r‚ژپ{‚Pپ…(‚‹پ{‚P)‚Qپ@پEپEپEپE‡@
‚·‚é‚ئپA‚پ‚ژپ{‚PپپS‚ژپ|‚Pپ\‚“‚ژپ…(‚‹پ{‚P)‚Qپ\‚‹‚Q
پ@پ@Œج‚ةپ@‚پ‚ژپ{‚Pپ…‚Q‚‹پ{‚P
’è‹`‚جژ®‚و‚èپ@a‚ژپ…‚پ‚ژپ{‚Pپ|‚Q
Œج‚ةپ@پ@پ@پ@پ@a‚ژپ…‚Q‚‹پ|‚P
پ@پ@پ@پ@پ@پ@پ@a‚ژپ|‚Pپ…‚Q‚‹پ|‚R
پ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپEپEپE
پ@پ@پ@پ@پ@پ@پ@a‚Rپ…پi‚Q‚‹پ{‚Pپjپ|‚Qپi‚ژپ\‚Qپj
پ@پ@پ@پ@پ@پ@پ@a‚Qپ…پi‚Q‚‹پ{‚Pپjپ|‚Qپi‚ژپ\‚Pپjپپ‚ک
‚±‚±‚إپA‚ک‚ج’l‚ة‚و‚ء‚ؤپAپuڈêچ‡•ھ‚¯پv‚·‚éپB
پi‚Pپjپ@‚کپپ‚R‚ج‚ئ‚«
پ@پ@پ@پ@‚±‚ج‚ئ‚«پ@a‚Rپ…‚Tپ@‚ئ‚ب‚éپB
پ@پ@ˆê•ûپ@پoa‚ژپp‚ج’è‹`ژ®‚و‚èپA‚پ‚Qپپ‚Rپ@پC‚پ‚Rپ†‚پ‚Qپ{‚Qپپ‚T‚إ‚ ‚é‚©‚çپA‚پ‚Rپپ‚Tپ@
پ@ˆب‰؛“¯—l‚ة‚µ‚ؤپA‚±‚جڈêچ‡‚ة‚حڈم‚ج•s“™چ†پ…‚ح‚·‚ׂؤپپ‚ئ‚ب‚éپB‚·‚é‚ئپA
‚پ‚ژپ{‚Pپ{‚پ‚ژپ{پEپEپE‚پ‚Rپ{‚پ‚Pپپپi‚Q‚‹پ{‚Pپjپ{پi‚Q‚‹پ|‚Pپjپ{پEپEپEپ{‚Rپ{‚Q
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ„پi‚Q‚‹پ{‚Pپjپ{پi‚Q‚‹پ|‚Pپjپ{پEپEپEپ{‚Rپ{‚P
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پپ(‚‹پ{‚P)‚Q
Œج‚ةپ@پ@پ@پ@‚r‚ژپ{‚Pپ„(‚‹پ{‚P)‚Q‚ئ‚ب‚èپA‡@پ@‚ة–µڈ‚‚·‚éپB
پi‚Qپj‚کپ„‚R‚ج‚ئ‚«
پ@پ@پ@‚ک‚حٹïگ”‚و‚èپ@a‚Rپ…‚Tپ@‚ئ‚ب‚éپB‚·‚é‚ئپA
‚پ‚ژپ{a‚ژپ|‚Pپ{پEپEپE‚پ‚Rپ{‚پ‚Pپ…پi‚Q‚‹پ\‚Pپjپ{پi‚Q‚‹پ|‚Rپjپ{پEپEپEپ{‚Tپ{‚Q
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پƒپi‚Q‚‹پ\‚Pپjپ{پi‚Q‚‹پ|‚Rپjپ{پEپEپEپ{‚Tپ{‚Rپ{‚P
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پپ‚‹‚Q
Œج‚ةپ@پ@پ@پ@‚r‚ژپƒ‚‹‚Q‚ئ‚ب‚èپA‡@پ@‚ة–µڈ‚‚·‚éپB
پi‚PپjپAپi‚Qپj‚¢‚¸‚ê‚جڈêچ‡‚ة‚à–µڈ‚‚ھگ¶‚¶‚ؤپAپuˆê”ت‰»پv‚µ‚½ڈم‚ج–â‘è‚ھڈط–¾‚³‚ꂽ‚±‚ئ‚ة‚ب‚éپBپ@ڈط–¾ڈI‚ي‚èپB
