�ߘa�Q�N�Q���P�U��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��38�Q�����w�I�ȉ����
�@�@�@�@����W���ԁF�P��19���`�Q��16����
�m�K�����̂���Ɍ��l�n
�ߋ��ɍw�ǂ��Ă����u�������w�v�̑�40��2000�N9�����̒��ŁA�m�����ꂳ��̌��e���Q�l�ɂ��āA��₵�܂����B


2020�N�Ɉ����̉���͕ʂ̃t���C���ɂ��܂����B
http://ryugen3.sakura.ne.jp/kadai12/kadai382b.htm
�������������������B
NO1�u���N���̂�������v 01/20 15��17���@��M �X�V 2/16
382�@���N���̂�������
���1
![]()
�܂��́A
![]()
���2
![]()
![]()
�܂��́A
![]()
�Ƃ����ƁA
![]()
�E�ӂ́A
![]()
![]()
�����ŁA
![]()
![]()
����āA
![]()
���3
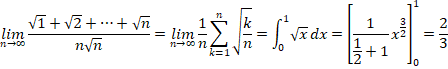
���4
![]()
�Ƃ����ƁA
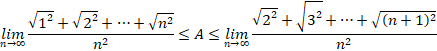
�E�ӂ́A
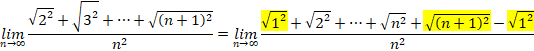
![]()
�����ŁA
![]()
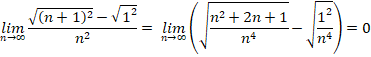
����āA
![]()
���5
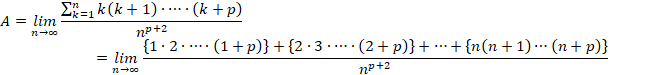
�Ƃ����ƁA
![]()
�E�ӂ́A
![]()
![]()
![]()
�����ŁA
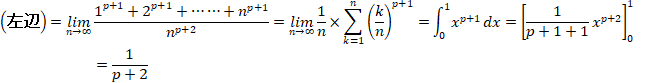
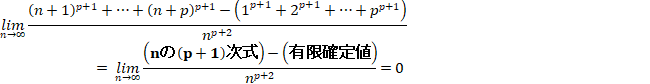
����āA
![]()
���6
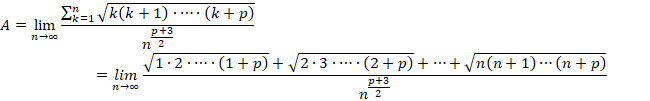
�Ƃ����ƁA
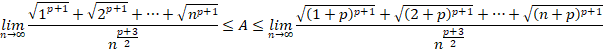
�E�ӂ́A
![]()
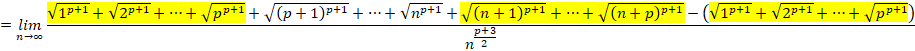
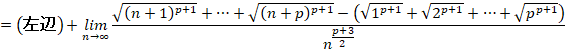
�����ŁA
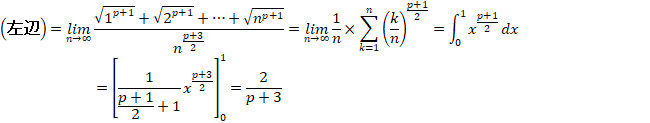
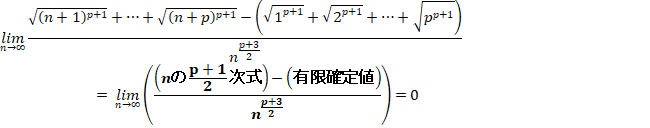
����āA
![]()
NO2�u�X���[�N�}���v 01/25 17��44���@��M
�X�V 2/16
(1)
n(n+1)/(2n^2)=n^2/(2n^2)+1/(2n^2)
so�c1/2
(2)
��k(k+1)����k^2+��k
=n(n+1)(2n+1)/6+n(n+1)/2
or
(1/n)^2+(2/n)^2+�c+(n/n)^2<?<(n/(n+1))^2*{(2/(n+1)}^2+(3/(n+1))^2+�c+(n+1)/(n+1))^2}
��[0,1]x^2 dx<?<��[0,1]x^2 dx
so�c1/3
(3)
��[0,1]��x*dx=[x^(3/2)/(1/2+1)]=2/3
(4)
(1/n)+(2/n)+�c+(n/n)<?<((n+1)/n)*{2/(n+1)+3/(n+1)+�c+(n+1)/(n+1)}
��[0,1]xdx<?<(n+1)/n*��[0,1]xdx
so�c1/2
(5)
(1/n)^(p+1)+(2/n)^(p+1)+�c+(n/n)^(p+1)<?<(n/(n+1))^(p+1)*{(2/(n+1))^(p+1)+(3/(n+1))^(p+1)+�c+((n+1)/(n+1))^(p+1)}
so�c
��[0,1]x^(p+1) dx<?<��[0,1]x^(p+1) dx
so�c
1/(p+2)
(6)
(1/n)^(p+1)/2+(2/n)^(p+1)/2+�c+(n/n)^(p+1)/2<?<((n+1)/n)^(p+1)/2*{(2/(n+1))^(p+1)/2+(3/(n+1))^(p+1)/2+�c+((n+1)/(n+1))^(p+1)/2}
so�c
��[0,1] x^(p+1)/2 dx
=2/(p+3)
NO3�u�l�c�����v
02/10 10��02���@��M �X�V 2/16
���P
�@�@(�P�{�Q�{�R�{�E�E�E�{��)�^���Q
�@�@�@��{�P�^�Q�E��(���{�P)}�^���Q
�@�@�@���P�^�Q�E(�P�{�P�^��)
�@�@�@���P�^�Q�i�������j
���Q
�@�@{�P�E�Q�{�Q�E�R�{�R�E�S�{�E�E�E�{���E(���{�P)}�^���R
�@�@�@���P�^���R�E���P����������(���{�P)
�@�@�@���P�^���R�E���P��������(���Q�{��)
�@�@�@���P�^���R�E{�P�^�U�E��(���{�P)(�Q���{�P)�{�P�^�Q�E��(���{�P)}
�@�@�@���P�^�U�E(�P�{�P�^��)(�Q�{�P�^��)�{�P�^�Q�E(�P�^���{�P�^���Q)
�@�@�@���P�^�R�i�������j
���R
�@�@lim������(��P�{��Q�{��R�{�E�E�E�{�ゎ)�^(���ゎ)
�@�@�@��lim������{(�P�^��)�P�^�Q�{(�Q�^��)�P�^�Q�{(�R�^��)�P�^�Q�{�E�E�E�{(���^��)�P�^�Q}�^��
�@�@�@��lim�������P�^���E���P��������(���^��)�P�^�Q
�@�@�@�����O�������P���P�^�Q����
�@�@�@���Q�^�R�E[���R�^�Q]�O�������P
�@�@�@���Q�^�R
���S
�@�����O�̂Ƃ��C���Q����(���{�P)��(���{�P)�Q���C
�@�@����{��(���{�P)}�P�^�Q�����{�P
�@�����P�C�Q�C�R�C�E�E�E�C���������C�ӁX��������ƁC
�@�@�P�^�Q�E��(���{�P)�����P��������{��(���{�P)}�P�^�Q���P�^�Q�E��(���{�P)�{�����P�^�Q�E��(���{�R)
�@���Q���O����C
�@�@�P�^�Q�E(�P�{�P�^��)���P�^���Q�E���P��������{��(���{�P)}�P�^�Q���P�^�Q�E(�P�{�R�^��)
�@�������Ƃ���ƁC�ō��ӁC�ʼnE�ӂ͋��ɂP�^�Q�Ɏ�������̂ŁC�͂��݂����̌������C
�@�@lim�������P�^���Q�E���P��������{��(���{�P)}�P�^�Q���P�^�Q
�@���C���P�`�S�̎��̕���̎����́C���ꂼ��C
�@�@�Q�C�R�C�R�^�Q�C�Q
�ƂȂ�C���̋t���ƂȂ��Ă���D
���T
�@���P�`������萔�Ƃ��āC
�@�@��(���{�P)(���{�Q)�E�E�E(���{��)�������{�P�{���P�����{���Q�����|�P�{�E�E�E�{������
�Ƃ���ƁC
�@�@�P�^�����{�Q�E���P����������(���{�P)(���{�Q)�E�E�E(���{��)
�@�@�@���P�^�����{�Q�E���P��������(�����{�P�{���P�����{���Q�����|�P�{�E�E�E�{������)
�@�@�@���P�^�����{�Q�E���P�������������{�P�{���P�E�P�^�����{�Q�E���P�������������{���Q�E�P�^�����{�Q�E���P�������������|�P
�@�@�@�@�@�{�E�E�E�{�����E�P�^�����{�Q�E���P����������
�@�����ŁC�P���������C���͐����Ƃ���ƁC
�@�@lim�������P�^�����{�Q�E���P������������
�@�@�@��lim�������P�^�����{�P�|���E�P�^���E���P��������(���^��)��
�@�@�@��lim�������P�^�����{�P�|���Elim�������P�^���E���P��������(���^��)��
�@�@�@���O�E���O�������P��������
�@�@�@���O
�@�@��lim�������P�^�����{�Q�E���P����������(���{�P)(���{�Q)�E�E�E(���{��)
�@�@�@�@��lim�������P�^�����{�Q�E���P��������(�����{�P�{���P�����{���Q�����|�P�{�E�E�E�{������)
�@�@�@�@��lim�������P�^�����{�Q�E���P�������������{�P�{���P�E�O�{���Q�E�O�{�E�E�E�{�����E�O
�@�@�@�@��lim�������P�^���E���P��������(���^��)���{�P
�@�@�@�@�����O�������P�����{�P����
�@�@�@�@���P�^(���{�Q)�E[�����{�Q]�O�������P
�@�@�@�@���P�^(���{�Q)
�i�m���ɕ���̎w�����C���̋t���ƂȂ��Ă���j
���U
�@�����O�̂Ƃ��C���R�Ɠ����ƂȂ�C�Q�^�R
�@�����O�̂Ƃ��C���T�Ɠ��l�ɁC
�@�@��(���{�P)(���{�Q)�E�E�E(���{��)�������{�P�{���P�����{���Q�����|�P�{�E�E�E�{������
�Ƃ���D
�@�����O�C�����O�̂Ƃ��C(���{��)�P�^�Q���め�{�も�ł���C�������O�i�P���������j�ł��邩��C
�@�@��(���{�P)�^�Q��{��(���{�P)(���{�Q)�E�E�E(���{��)}�P�^�Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@����(���{�P)�^�Q�{�め�P�E�����^�Q�{�め�Q�E��(���|�P)�^�Q�{�E�E�E�{�め���E���P�^�Q�E�E�E(1)
�@�����ŁC
�@�@lim�������P�^��(���{�R)�^�Q�E���P����������(���{�P)�^�Q
�@�@�@��lim�������P�^���E���P��������(���^��)(���{�P)�^�Q
�@�@�@�����O�������P��(���{�P)�^�Q����
�@�@�@���Q�^(���{�R)�E[��(���{�R)�^�Q]�O�������P
�@�@�@���Q�^(���{�R)
�@�@lim�������P�^��(���{�R)�^�Q�E���P��������{��(���{�P)�^�Q�{�め�P�E�����^�Q�{�め�Q�E��(���|�P)�^�Q�{�E�E�E�{�め���E���P�^�Q}
�@�@�@��lim�������P�^���E���P��������(���^��)(���{�P)�^�Q
�@�@�@�@�@�{�め�P�Elim�������P�^���P�^�Q�E�P�^���E���P��������(���^��)���^�Q
�@�@�@�@�@�{�め�Q�Elim�������P�^���E�P�^���E���P��������(���^��)(���|�P)�^�Q
�@�@�@�@�@�{�E�E�E
�@�@�@�@�@�{�め���Elim�������P�^�����^�Q�E�P�^���E���P��������(���^��)�P�^�Q
�@�@�@���Q�^(���{�R)�{�め�P�E�O�{�め�Q�E�O�{�E�E�E�{�め���E�O
�@�@�@���Q�^(���{�R)
�@(1)���C�͂��݂����̌�������C
�@�@lim�������P�^��(���{�R)�^�Q�E���P��������{��(���{�P)(���{�Q)�E�E�E(���{��)}�P�^�Q���Q�^(���{�R)
�@����́C�����O�̏ꍇ���܂ށD
�i����̎w�����C���̋t���ƂȂ��Ă���j
NO3�u�W���[�J�[�v
02/12 17��42���@��M �X�V 2/16


NO4�u�O�p��K�v�@�@�@�@ 02/15 10��59���@��M �X�V 2/16

NO5�u���̗���v�@�@�@�@ 02/22 17���@ �X�V 2/122
�F����̉ɒ��S���[�������\���グ�܂��B
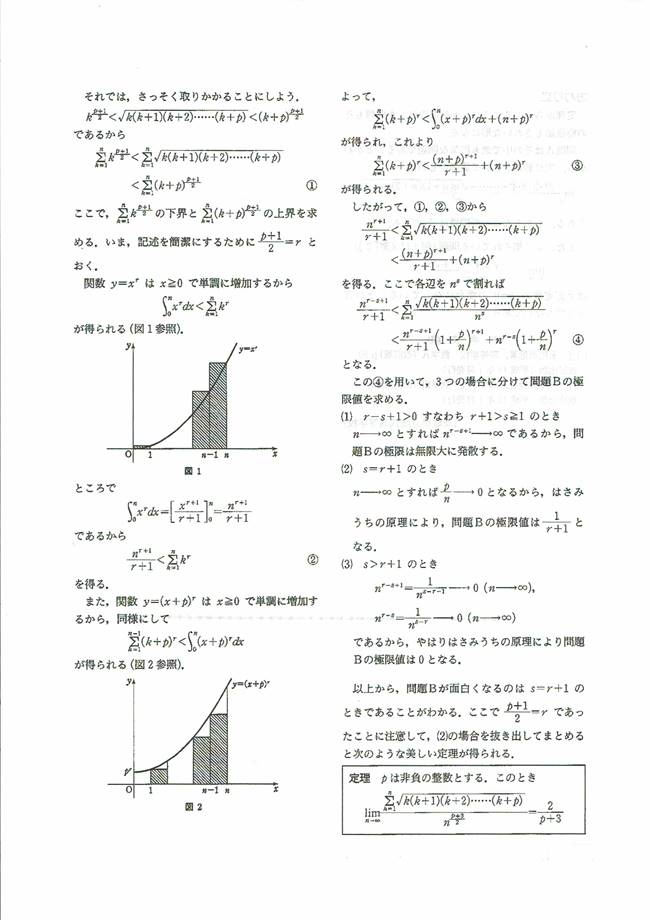
���āA���P������S�܂ł́A���������̋Ɍ��l�ƒ�ϕ��̌�����p������z�肵�Ă��܂����B�����ŁA��ʂ̏ꍇ�����T�Ɩ��U�ł��B
������̗\�肵�Ă����͖��5�Ɋւ��Ắu�W���[�J�[�v��u�O�p��K�v�Ɠ����ň�ʂ̘A�����鎩�R���̐ς̘a�̎��𗘗p���ċ��߂��@�ł��B
���U�Ɋւ��ẮA�m�����ꂳ�A����Ɉ�ʂ̏ꍇ���l���ē��e����Ă��܂��̂ŁA���̉��ڂ��Ă����܂��B
�@
�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
