�ߘa�Q�N�Q���Q�R��
 [���ꐯ]
[���ꐯ]
�@�@�@�@��382�����w�I�ȉ����
�@�@�@�@����W���ԁF�P��19���`�Q��16����
�m2020�N�̖��n
�u�W���[�J�[�v����A�O��A����2020�N�Ɉ���肪���܂����B

NO1�u���N���̂�������v 01/23 18��28���@��M �X�V 2/23
2020�N�Ɉ����@�@���N���̂�������
���悸�A���������܂��B
������![]() �𐮊��ɓW�J���܂��B
�𐮊��ɓW�J���܂��B
![]()
�Ƃ���ƁA
![]()
![]()
![]() ���
���
����āA
![]()
���āA
![]() �Ƃ��܂��B
�Ƃ��܂��B
![]()
![]()
![]() �@�@���
�@�@���
����āA
![]()
![]()
����ƁA
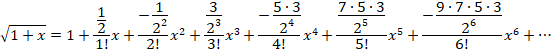
![]()
��44�~44=1936�A45�~45=2025�ł��B
(1)
![]()
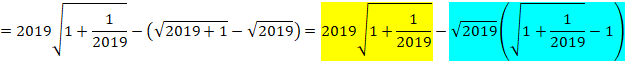
���������ׂ܂��B
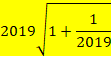
![]()
�Ȃ̂ŁA���������́A
![]()
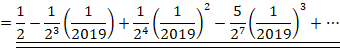
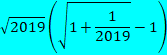
![]()
![]()
![]()
![]()
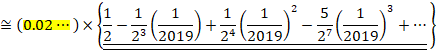
���F�̕����̏����ɁA�̕����̏����͑傫�ȉe����^���Ȃ��̂ŁA�����́A2019�ł��B
(2)
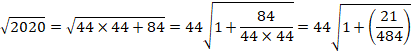
![]() �̏��������́A
�̏��������́A![]() �ł��B
�ł��B
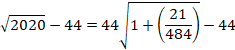
![]()
![]()
![]()
![]()
���
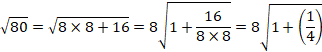
![]() �̏��������́A
�̏��������́A![]() �ł��B
�ł��B
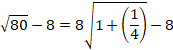
![]()
![]()
![]()
![]()
�ȏォ��A![]() �̏��������̕����傫���ł��B
�̏��������̕����傫���ł��B
(3)
2�d�����́A���̂悤�ɊO���܂��B
![]()
 �@�i���̂Ƃ��̑召�͋t�ł��j
�@�i���̂Ƃ��̑召�͋t�ł��j
![]() �ł��B
�ł��B
���āA
![]()
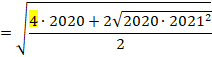
2020��2021�́A����Ȃɕς��Ȃ��̂ŁA�ς�![]() �ƂȂ铙����2���������߂Ɍ��ς���ƁA
�ƂȂ铙����2���������߂Ɍ��ς���ƁA
44�E2020�ł�
�a�́A2�~44�E2020��88�E2020(��4�E2020) �Ȃ̂Ŏ����͈̔͂ł͊O���܂���B
(4)
�ꏊ��\���̂ɁA1�̈ʂ���(��)���ڂŕ\�����Ƃɂ��܂��B
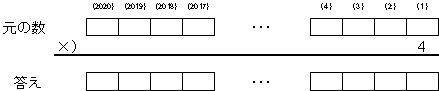
�|���Z�̕��K�����܂��B
![]()
���̌��ɌJ��オ��ꍇ�́A�o1�A2�A3�p��3�ʂ�ł��B
�����̐���(2020)���̂Ƃ���́A�J��肪�Ȃ��̂Ło1�A2�p�̂ǂ��炩�ł��B
�E���̐���(2020)�́A1�ł͂���܂���B
�@1���Ƃ���ƁA������(2020)�́A�o4�A5�A6�A7�p�̂ǂꂩ�ł��B
�@4�̂Ƃ��A���̐���(1)��4�ƂȂ�A4�~4��16�A�ŕs�K�ł��B
�@5�̂Ƃ��A���̐���(1)��5�ƂȂ�A5�~4��20�A�ŕs�K�ł��B
�@6�̂Ƃ��A���̐���(1)��6�ƂȂ�A6�~4��24�A�ŕs�K�ł��B
�@7�̂Ƃ��A���̐���(1)��7�ƂȂ�A7�~4��28�A�ŕs�K�ł��B
�@�ȏォ��ł��B
�E���̐���(2020)�́A2�ł��B
�@2�̂Ƃ��A������(2020)�́A�o8�A9�p�̂ǂꂩ�ł��B
�@8�̂Ƃ��A���̐���(1)��8�ƂȂ�A8�~4��32�A�œK���܂��B
�@9�̂Ƃ��A���̐���(1)��9�ƂȂ�A9�~4��36�A�ŕs�K�ł��B
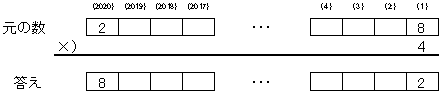
�����̐���(2020)�́A2�ł��B
�����̐���(2019)�́A�J��肪�Ȃ��̂Ło1�A2�p�̂ǂ��炩�ł��B
�E2�ł͂���܂���B
�@2���Ƃ���ƁA������(2019)�́A�o8�A9�p�̂ǂꂩ�ł��B
�@8�̂Ƃ��A���̐���(2)��8�ƂȂ�A8�~4�{3��35�A�ŕs�K�ł��B
�@9�̂Ƃ��A���̐���(2)��9�ƂȂ�A9�~4�{3��39�A�ŕs�K�ł��B
�E���̐���(2019)�́A1�ł��B
�@1�̂Ƃ��A������(2019)�́A�o4�A5�A6�A7�p�̂ǂꂩ�ł��B
�@4�̂Ƃ��A���̐���(2)��4�ƂȂ�A4�~4�{3��19�A�ŕs�K�ł��B
�@5�̂Ƃ��A���̐���(2)��5�ƂȂ�A5�~4�{3��23�A�ŕs�K�ł��B
�@6�̂Ƃ��A���̐���(2)��6�ƂȂ�A6�~4�{3��27�A�œK���܂��B
�@7�̂Ƃ��A���̐���(2)��7�ƂȂ�A7�~4�{3��31�A�œK���܂��B
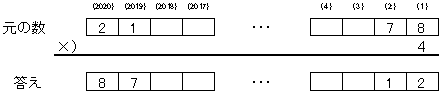
�����̐���(2019)�́A1�ł��B
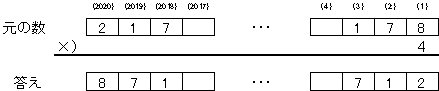
�����̐���(2018)�́A3�J��オ�肪����̂Ło7�A8�A9�p�̂ǂꂩ�ł��B
�E7���Ƃ���ƁA������(2018)�́A������R�J��オ�肪�����āo1�p�ł��B
�@1�̂Ƃ��A���̐���(3)��1�ƂȂ�A1�~4�{3��7�A�œK���܂��B
�@
�@�E���̂Ƃ��A����(2017)��3�J��オ��̂Ło7�A8�A9�p�̂ǂꂩ�ł��B
7���Ƃ���ƁA������(2017)�́A������R�J��オ��̏ꍇ������āo8�A9�A0�A1�p�ł��B
�@�@8�̂Ƃ��A���̐���(4)��8�ƂȂ�A8�~4��32�A�ŕs�K�ł��B
�@�@9�̂Ƃ��A���̐���(4)��9�ƂȂ�A9�~4��36�A�ŕs�K�ł��B
�@�@0�̂Ƃ��A���̐���(4)��0�ƂȂ�A0�~4��0�A�ŕs�K�ł��B
�@�@1�̂Ƃ��A���̐���(4)��1�ƂȂ�A1�~4��4�A�ŕs�K�ł��B
�@�@
8���Ƃ���ƁA������(2017)�́A������R�J��オ��̏ꍇ������āo2�A3�A4�A5�p�ł��B
�@ 2�̂Ƃ��A���̐���(4)��2�ƂȂ�A2�~4��8�A�œK���܂��B
�@�@3�̂Ƃ��A���̐���(4)��3�ƂȂ�A3�~4��12�A�ŕs�K�ł��B
�@�@4�̂Ƃ��A���̐���(4)��4�ƂȂ�A4�~4��16�A�ŕs�K�ł��B
�@�@5�̂Ƃ��A���̐���(4)��5�ƂȂ�A5�~4��20�A�ŕs�K�ł��B
�@
������݂�ƁA�����́u2178�v�������Ȃ̂ŁA2020��4��505 ��J��Ԃ����ł��B
�@�@![]()
9���Ƃ���ƁA������(2017)�́A������R�J��オ��̏ꍇ������āo6�A7�A8�A9�p�ł��B
�@ 6�̂Ƃ��A���̐���(4)��6�ƂȂ�A6�~4��24�A�ŕs�K�ł��B
�@�@7�̂Ƃ��A���̐���(4)��7�ƂȂ�A7�~4��28�A�ŕs�K�ł��B
�@�@8�̂Ƃ��A���̐���(4)��8�ƂȂ�A8�~4��32�A�ŕs�K�ł��B
�@�@9�̂Ƃ��A���̐���(4)��9�ƂȂ�A9�~4��36�A�ŕs�K�ł��B
�E8���Ƃ���ƁA������(2018)�́A������R�J��オ��̏ꍇ������āo2�A3�A4�A5�p�ł��B
�@2�̂Ƃ��A���̐���(3)��2�ƂȂ�A2�~4�{3��11�A�ŕs�K�ł��B
�@3�̂Ƃ��A���̐���(3)��3�ƂȂ�A3�~4�{3��15�A�ŕs�K�ł��B
�@4�̂Ƃ��A���̐���(3)��4�ƂȂ�A4�~4�{3��19�A�ŕs�K�ł��B
�@5�̂Ƃ��A���̐���(3)��5�ƂȂ�A5�~4�{3��23�A�ŕs�K�ł��B
�E9���Ƃ���ƁA������(2018)�́A������R�J��オ��̏ꍇ������āo6�A7�A8�A9�p�ł��B
�@6�̂Ƃ��A���̐���(3)��6�ƂȂ�A6�~4�{3��27�A�ŕs�K�ł��B
�@7�̂Ƃ��A���̐���(3)��7�ƂȂ�A7�~4�{3��31�A�ŕs�K�ł��B
�@8�̂Ƃ��A���̐���(3)��8�ƂȂ�A8�~4�{3��35�A�ŕs�K�ł��B
�@9�̂Ƃ��A���̐���(3)��9�ƂȂ�A9�~4�{3��39�A�œK���܂��B

�����́A(2020)��2�A(2019)��1�A(2)��7�A(1)��8�ŁA�Ȃ���2016�������ׂ�9�̐��ł��B
�@![]()
��̃p�^�[��������悤�ł��B
(5)
![]()
![]()
�̂悤�ɁA2���̊��̘a�͈��������ł��܂��B
2021��47�~43�ł��B
���āA�����̐���2�s�ɕ��ׂ܂��B
1�s�ڂ͏��������ɁA2�s�ڂ͑傫�����ɕ��ׂ܂��B
![]()
�����āA�㉺��2���������܂��B
�Ⴆ�A2��ڂ́A
![]()
![]()
![]()
![]()
�ǂ̗���A47�������ɂ��̂ŁA�]���0�ł��B
�u���N���̂�������v
03/20 23��50���@��M �X�V 3/21
2020�N�Ɉ����(4)�ɂ��ā@���N���̂�������
�������߂�ꂽ�̂ł͂���܂��A�l�����������܂��B
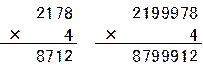
���E�̌v�Z�̂悤�ɁA4�������ĕ��т��t�ɂȂ鐔���p�^�[��
�Ƃ������Ƃɂ��܂��B
�p�^�[���͒�����9�����Ă���͂�p�^�[���ł��B
�p�^�[���̕���ł��鐔���̌����Ƃ������Ƃɂ��܂��B
�p�^�[��2178�̒�����4�A
 �p�^�[��2199978�̒�����7�ł��B
�p�^�[��2199978�̒�����7�ł��B
���������̃p�^�[���̊Ԃ�
0�����Ă��p�^�[���ɂȂ�܂��B
�p�^�[����0���������Ȃ������̂��u���b�N�Ƃ������Ƃɂ��܂��B
21780�A21978000�A����Ȃǂ��u���b�N�ł��B
�u���b�N�̐����̌�����͂�A�����Ƃ������Ƃɂ��܂��B
�����p�^�[���ɁA�E��0���Ȃ������́A����0���Ȃ������̂��Ȃ��Ă��p�^�[���ł��B
�Ⴆ�A21780��02178���Ȃ��āA2178002178�Ƃ������̂́A�p�^�[���ł��B
��2020���͌v�Z����ςȂ̂ŁA32���ŋ�̓I�ɂ݂Ă݂܂��B
�Z�p�^�[����1�̂Ƃ��́A2199���9978��1�ʂ�ł��B
21��78�̒��ɁA28��9�����т܂��B
�Z�p�^�[����2�̂Ƃ��́A2199��7800����b���002199��78 �̌`�����Ă��܂��B
�b�͒�����\���Ă��܂��B
�����̍��ƉE�ł́A�����p�^�[����0���E�ɂ��u���b�N�ƍ��ɂ��u���b�N���Ȃ����Ă��܂��B
���E�Ώ̂Ȃ̂ŁA����16���ōl���܂��B
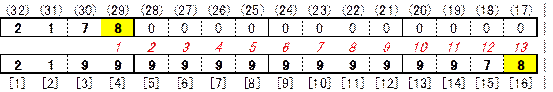
����16�̃u���b�N�̎�ނ𐔂��܂��B
8�̈ʒu���l����ƁA13�ʂ肠��܂��B
�u���b�N�����ʂ肠�邩�́A��������3���������܂�܂��B
�Z�p�^�[����3�̂Ƃ��́A (2199��7800��)(2199���b��9978)(���002199��78)�̌`�����Ă��܂��B
����k�̃u���b�N��2�A����2n�̃u���b�N��1�ł��B
n�́A2����12�̒l���Ƃ�܂��B�ik�̍ŏ��l��4�ł��j
k�̒����́A16�|n�ł��B
����āA����k�̃u���b�N����ނ́A16�|n�|3��13�|n
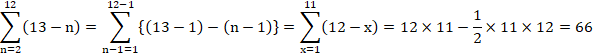
�Z�p�^�[����4�̂Ƃ��́A(2199��7800��)(2199��78)�b(2199��78)(���002199��78)�̌`�����Ă��܂��B
�������獶�ōl���܂��B
1�Ԗڂ̃u���b�N�̒�����n�Ƃ���ƁA2�Ԗڂ̃u���b�N�̒�����16�|n�ł��B
n�́A4����12�̒l���Ƃ�܂��B
1�Ԗڂ̃u���b�N�̎�ނ�n�|3�ʂ�A2�Ԗڂ̃u���b�N�̎�ނ�16�|n�|3��13�|n�ʂ�ł��B
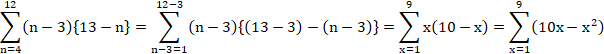
![]()
�Z�p�^�[����5�̂Ƃ��́A
(2199��7800��)(2199��7800��)(2199���b��9978)(��002199��78)(���002199��78)�̌`�����Ă��܂��B
����k�̃u���b�N��2�A����m�̃u���b�N��2�A����2n�̃u���b�N��1�ł��B
n�́A2����8�̒l���Ƃ�܂��B�ik�Am�̍ŏ��l��4�ł��j
1�Ԗڂ̃u���b�N�̒�����k�Ƃ���ƁAk��4����16�|n�|4��12�|n�̒l���Ƃ�܂��B
2�Ԗڂ̃u���b�N�̒�����16�|k�|n��16�|k�|n�ł��B
�����̃u���b�N�̒����́An�ł��B
1�Ԗڂ̃u���b�N�̎�ނ�k�|3�ʂ�ł��B
2�Ԗڂ̃u���b�N�̎�ނ�16�|k�|n�|3��13�|k�|n�ʂ�ł��B

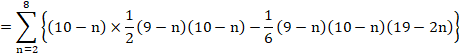
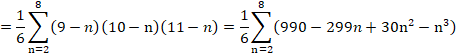
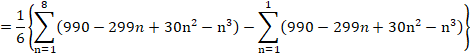
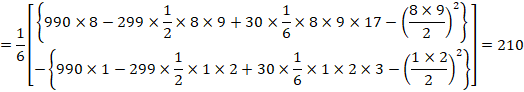
�Z�p�^�[����6�̂Ƃ��́A
(2199��7800��)(2199��78)(2199��78)�b(2199��78)(2199��78)(���002199��78)�̌`�����Ă��܂��B
�������獶�ōl���܂��B
1�Ԗڂ̃u���b�N�̒�����k�Ƃ���ƁAk��4����8�̒l���Ƃ�܂��B
2�Ԗڂ̃u���b�N�̒�����m�Ƃ���ƁAm��4����16�|k�|4��12�|k�̒l���Ƃ�܂��B
3�Ԗڂ̃u���b�N�͂̒����́A16�|k�|m�ł��B
1�Ԗڂ̃u���b�N�̎�ނ�k�|3�ʂ�ł��B
���ꂼ��ɑ��āA2�Ԗڂ̃u���b�N�̎�ނ�m�|3�ʂ�A
3�Ԗڂ̃u���b�N��16�|k�|m�|3=13�|k�|m�ʂ�ł��B
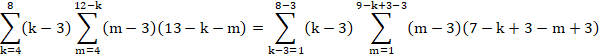
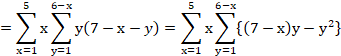
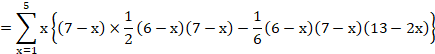
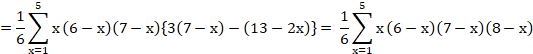
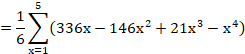
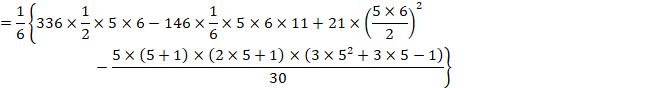
![]()
�Z�ȉ��͂���Ă��܂���B
�����̂悤�Ɍv�Z�͂���ʓ|�ɂȂ��Ă����܂��B
�����̌v�Z���܂Ƃ߂Ĉ����悤�ȕ��@�͌��������܂���B
�����̗���F�����Ƒ���Ȏ��Ԃ��₳�ꂽ���ƂɊ��Ӑ\���グ�܂��B����҂����ẴT�C�g�ł��B���肪�������Ƃł��B3��21���L��
NO2�u�X���[�N�}���v
01/25 17��44���@��M
�X�V 2/23
(1)
���炩�ɁA
-1<��2019-��2020<0
2019<��(2019*2020)<2020
��(2019*2020)-2019=��2019*(��2020-��2019)
so�c��2019*(��2020-��2019)-(��2020-��2019)= (��2020-��2019)(��2019-1)>0
�܂�A��(2019*2020)�̏������������A��2020-��2019�̏��������̕����������̂ŁA���ǁA�^���̐���������2019
(2)
8<��80<9
��80=9-r(80)�E�E�E���ۂ�(1-r(80))����80�̏�������
44^2=1936<��2020<45^2=2025
so�c
��2020=45-r(2020)
80*5^2=2000
so�c
r(2020)>5*r(80)
so�c
r(2020)>r(80)
so�c
��80�̏����̕����傫��
(3)
��2020*��(2*��2020+2021)
=��2020*(��2020+1)
=2020+��2020
�ƊO����B
(4)
2020=4*5*101
���オ�肪�Ȃ��̂��c
2?...?8 �ɂȂ���̂�T�����c
21978
So�c���ꂪ404��J��Ԃ�������
(5)
2021=47*43
so�c
(2021-1)^2019��2020^2019��-1^2019
(2021-2)^2019��2019^2019��-2^2019
�c
(2021-1010)^2019��1011^2019��-1010^2019
����A�^����0 (mod 47)
�u�X���[�N�}���v 01/31 21��40���@��M
�X�V 2/16
2020�N�Ɉ����
(3)�čl�c
(4)�͗F�l����̂��̂ł��c
(3)�^��=��{(2020+��2020)+��2020(2020+��2020)}
�@�@�@=��{(2020+��2020)*(��2020+1)}
�@�@�@=(2020+��2020)/(2020)^(1/4)
=(2020)^(3/4)+(2020)^(1/4)
(4)�@X00�c�c�c�c�c00X�@�Ƃ���
�@�@X*4�@��X��
�t���ɂȂ��Ă���Ώ��������B
�@�@X��1�A2�A3���ł͂Ȃ��@4���ł�2178�@5���ł�21978�@��OK
�@�i21780000�c�c00002178�j
�@�������炪�J��Ԃ����荬�݂��Ă��Ă�OK�ŁA���̂ق�
5���Ƃ���Ǝv���܂����B
NO3�u�l�c�����v
02/10 10��02���@��M �X�V 2/23
�Q�O�Q�O�N���
�i�P�j�P�X�R�U���S�S�Q���Q�O�P�X���Q�O�Q�O���Q�O�Q�T���S�T�Q���C
�@�@�S�S����Q�O�P�X����Q�O�Q�O���S�T
�@�Q�O�P�X�Q���Q�O�P�X�E�Q�O�Q�O���Q�O�Q�O�Q���C�Q�O�P�X��(�Q�O�P�X�E�Q�O�Q�O)�P�^�Q���Q�O�Q�O
�@��Q�O�P�X�C��Q�O�Q�O�C(�Q�O�P�X�E�Q�O�Q�O)�P�^�Q�̏������������ꂼ�ꂁ�C���C���Ƃ���ƁC
�@�@��Q�O�P�X���S�S�{���C��Q�O�Q�O���S�S�{���C(�Q�O�P�X�E�Q�O�Q�O)�P�^�Q���Q�O�P�X�{���C
�@�@�O�����������P�C�O�������P
�@�@����Q�O�P�X�|��Q�O�Q�O�{(�Q�O�P�X�E�Q�O�Q�O)�P�^�Q��(�S�S�{��)�|(�S�S�{��)�{(�Q�O�P�X�{��)
�@�@�@�@���Q�O�P�X�{(���|���{��)�E�E�E(1)
�@�����ŁC
�@�@���|���{����(��Q�O�P�X�|�S�S)�|(��Q�O�Q�O�|�S�S)�{{(�Q�O�P�X�E�Q�O�Q�O)�P�^�Q�|�Q�O�P�X}
�@�@�@��(��Q�O�P�X�|��Q�O�Q�O)�{��Q�O�P�X�E(��Q�O�Q�O�|��Q�O�P�X)
�@�@�@��(��Q�O�Q�O�|��Q�O�P�X)(��Q�O�P�X�|�P)���O
�@�@�P�|(���|���{��)���P�{(��Q�O�P�X�|��Q�O�Q�O)(��Q�O�P�X�|�P)
�@�@�@���P�{�Q�O�P�X�|(��Q�O�Q�O�{�P)��Q�O�P�X�{��Q�O�Q�O
�@�@�@����Q�O�Q�O�E(��Q�O�Q�O�{�P)�|(��Q�O�Q�O�{�P)��Q�O�P�X
�@�@�@��(��Q�O�Q�O�|��Q�O�P�X)(��Q�O�Q�O�{�P)���O
�@�@���O�����|���{�����P
�@(1)���C�^���̐��������́C�Q�O�P�X�ł���D
�i�Q�j�P�X�R�U���Q�O�Q�O���Q�O�Q�T���C�S�S����Q�O�Q�O���S�T
�@�U�S���W�Q���W�O���W�P���X�Q���C�W����W�O���X
�@��Q�O�Q�O�C��W�O�̏������������ꂼ�ꂁ�C���Ƃ���ƁC
�@�@��Q�O�Q�O���S�S�{���C��W�O���W�{���C�O�������P�C�O�������P
�@�@��������Q�O�Q�O�|�S�S�C������W�O�|�W
�@�@�����|����(��Q�O�Q�O�|�S�S)�|(��W�O�|�W)���Q��T�O�T�|�S��T�|�R�U
�@�@�@�@���Q{��T�O�T�|�Q(��T�{�X)}�E�E�E(1)
�@�����ŁC
�@�@(��T�O�T)�Q�|{�Q(��T�{�X)}�Q���T�O�T�|�S(�T�{�P�W��T�{�W�P)
�@�@�@���P�U�P�|�V�Q��T����Q�T�X�Q�P�|��Q�T�X�Q�O���O
�@�@��(��T�O�T)�Q��{�Q(��T�{�X)}�Q
�@�@����T�O�T���Q(��T�{�X)
�@(1)���C���|�����Q{��T�O�T�|�Q(��T�{�X)}���O
�@�@��������
�@�̂Ɂ�Q�O�Q�O�̏��������̕����傫���D
�i�R�j(�Q�O�Q�O�{�Q�O�Q�O�{��Q�O�Q�O�{�Q�O�Q�O��Q�O�Q�O)�P�^�Q
�@�@�@�@��{��Q�O�Q�O�E(�Q��Q�O�Q�O�{�P�{�Q�O�Q�O)}�P�^�Q
�@�@�@�@���Q�O�Q�O�P�^�S�E{(��Q�O�Q�O�{�P)�Q}�P�^�Q
�@�@�@�@���Q�O�Q�O�P�^�S�E(��Q�O�Q�O�{�P)
�@�@�@�@���Q�O�Q�O�R�^�S�{�Q�O�Q�O�P�^�S
�@�̂ɓ�d�������O�����Ƃ��ł���D
�i�S�j�Q���̐��̏ꍇ�Ōv�Z����D
�@�S(�P�O���{��)���P�O���{���i���C���͐����C�P�������X�C�P�������X�j�Ƃ���ƁC
�@�@�R�X�����U��
�@�@���P�R�����Q���E�E�E(1)
�@�P�R�C�Q�݂͌��ɑf�Ȃ̂ŁC���͂P�R�̔{���D
�@����͂P�������X�ɖ�������D
�@�S���̐��̏ꍇ�Ōv�Z����D
�@�@�S(�P�O�O�O���{�P�O�O���{�P�O���{��)���P�O�O�O���{�P�O�O���{�P�O���{���C
�@�@���C���C���C���͐����C�P�������X�C�O�������X�C�O�������X�C�P�������X
�Ƃ���ƁC
�@�@�R�X�X�X���{�R�X�O�����U�O���{�X�X�U��
�@�@���P�R�R�R�����Q�O���{�R�R�Q���|�P�R�O�����Q(�P�O���{�P�U�U���|�U�T��)�E�E�E(2)
�@�P�R�R�R�C�Q�݂͌��ɑf�Ȃ̂ŁC���͂Q�̔{���D
�@�����X�C�����X�C�|�����O����C
�@�@�P�R�R�R�����Q(�P�O���{�P�U�U���|�U�T��)���Q(�P�O�E�X�{�P�U�U�E�X�|�U�T�E�O)���R�P�U�W
�@�@�������R�P�U�W�^�P�R�R�R���Q�{�T�O�Q�^�P�R�R�R
�@�ȏ���C�����Q
�@(2)���C�P�R�R�R���P�O���{�P�U�U���|�U�T���E�E�E(3)
�@�@���U�T�����Q(�T���{�W�R��)�|�P�R�R�R
�@�̂ɂU�T���͊�ł���C���͊�ł���D
�@(3)���C
�@�@�U�T�����P�O���{�P�U�U���|�P�R�R�R���P�O�E�X�{�P�U�U�E�X�|�P�R�R�R���Q�T�P
�@�@�������Q�T�P�^�U�T���R�{�T�U�^�U�T
�@�ȏ���C�����P�C�R
i). �����P�̂Ƃ��C(3)���C�P�R�X�W���P�O���{�P�U�U��
�@�@���U�X�X���T���{�W�R���E�E�E(4)
�@�@���T���߂S�|�R���߂O�imod �T�j
�@�@�������R�C�W
�@�T�����U�X�X�|�W�R�����T�E�X���S�T���C
�@�@�����U�T�S�^�W�R���V�{�T�R�^�W�R
�@�@�������W
�@�ȏ���C�����W
�@(4)���C�T�����U�X�X�|�W�R�E�W���R�T
�@�@�������V
�@�̂ɂS���̐����́C�Q�P�V�W
�@�̂ɂQ�O�Q�O���̐����ł́C���̂Q�P�V�W���C���̏��łT�O�T��J��Ԃ��悢�D
ii). �����R�̂Ƃ��C(3)���C�P�T�Q�W���P�O���{�P�U�U��
�@�@���V�U�S���T���{�W�R���E�E�E(4)
�@�@���T���߂S�|�R���߂O�imod �T�j
�@�@�������R�C�W
�@�T�����V�U�S�|�W�R�����S�T���C�����V�P�X�^�W�R���W�{�T�T�^�W�R
�@����͂����R�C�W�ɖ�������D
�@�܂��C���̂Q�P�V�W�𗘗p���āC
�@�@�Q�P�X�V�W�C�Q�P�X�X�V�W�C�Q�P�X�X�X�V�W�C�E�E�E
���C���̐����������Ă��邱�Ƃ�������D
�@�̂ɁC�Q�P�̎��ɁC�X���Q�O�P�U��J��Ԃ��āC�Ō�ɂV�W��t�����������ł���D
�@�ȏ���C
�@�@�Q�P�V�W���C���̏��łT�O�T��J��Ԃ����Q�O�Q�O���̐���
�@�@�Q�P�̎��ɁC�X���Q�O�P�U��J��Ԃ��āC�Ō�ɂV�W��t�����Q�O�Q�O���̐���
�����ł���D
�u�l�c�����v
02/10 10��20���@��M �X�V 2/16
�Q�O�Q�O�N���i�S�j�i�ʉ��j
�@�W���̏ꍇ��VBSCRIPT�̃v���O�����ʼn����Ă݂�D
dim a(9)
a(0)=0:a(9)=""
call saiki(1,a)
msgbox a(9)
'
sub saiki(n,a())
if n=1 or n=8 then
a(n)=1
else
a(n)=0
end if
while a(n)<=9
if n<8 then
call saiki(n+1,a)
else
call check(a)
end if
a(n)=a(n)+1
wend
end sub
sub check(a())
dim b(8),c(8)
for j=1 to 8
b(j)=a(j)*4:c(j)=a(8+1-j)
next
for j=1 to (8-1)
b(j+1)=b(j+1)+b(j)\10:b(j)=b(j) mod 10
next
dame=0
for j=1 to 8
if b(j)>
end if
next
if dame=0 then
a(0)=a(0)+1
if a(0)>1 then a(9)=a(9)&chr(13)
for j=8 to 1 step -1
a(9)=a(9)&a(j)
next
end if
end sub
�@���̌��ʂ��C�S���̐��Q�P�V�W�C�W���̐��Q�P�V�W�Q�P�V�W���C���̐�����L���C�Q�P�X�X�X�X�V�W�����̐�����L���邱�Ƃ�������D
�@�ȏ�ɂ��
�C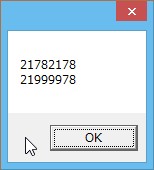
�@�@�Q�P�V�W���C���̏��łT�O�T��J��Ԃ����Q�O�Q�O���̐���
�@�@�Q�P�̎��ɁC�X���Q�O�P�U��J��Ԃ��āC�Ō�ɂV�W��t�����Q�O�Q�O���̐���
�����ł���D
�u�l�c�����v
02/12 10��17���@��M �X�V 2/16



�u�l�c�����v
02/17 08��57���@��M �X�V 2/23
�Q�O�Q�O�N���i�T�j
�@�ȉ�mod �S�V�Ōv�Z����D
�@�@�P�Q�O�P�X�{�Q�Q�O�P�X�{�R�Q�O�P�X�{�E�E�E�{�Q�O�Q�O�Q�O�P�X
�@�@�@��{(�S�V�E�O�{�P)�Q�O�P�X�{(�S�V�E�O�{�Q)�Q�O�P�X�{(�S�V�E�O�{�R)�Q�O�P�X�{�E�E�E�{(�S�V�E�O�{�S�U)�Q�O�P�X}
�@�@�@�@�@�{{(�S�V�E�P�{�P)�Q�O�P�X�{(�S�V�E�P�{�Q)�Q�O�P�X�{(�S�V�E�P�{�R)�Q�O�P�X�{�E�E�E�{(�S�V�E�P�{�S�U)�Q�O�P�X}
�@�@�@�@�@�{{(�S�V�E�Q�{�P)�Q�O�P�X�{(�S�V�E�Q�{�Q)�Q�O�P�X�{(�S�V�E�Q�{�R)�Q�O�P�X�{�E�E�E�{(�S�V�E�Q�{�S�U)�Q�O�P�X}
�@�@�@�@�@�{�E�E�E
�@�@�@�@�@�{{(�S�V�E�S�Q�{�P)�Q�O�P�X�{(�S�V�E�S�Q�{�Q)�Q�O�P�X�{(�S�V�E�S�Q�{�R)�Q�O�P�X�{�E�E�E�{(�S�V�E�S�Q�{�S�U)�Q�O�P�X}
�@�@�@�߂S�R(�P�Q�O�P�X�{�Q�Q�O�P�X�{�R�Q�O�P�X�{�E�E�E�{�S�U�Q�O�P�X)
�@�@�@�߂S�R[(�P�Q�O�P�X�{�Q�Q�O�P�X�{�R�Q�O�P�X�{�E�E�E�{�Q�R�Q�O�P�X)
�@�@�@�@�@�{{(�|�Q�R)�Q�O�P�X�{(�|�Q�Q)�Q�O�P�X�{(�|�Q�P)�Q�O�P�X�{�E�E�E�{(�|�P)�Q�O�P�X}]
�@�@�@���S�R{(�P�Q�O�P�X�{�Q�Q�O�P�X�{�R�Q�O�P�X�{�E�E�E�{�Q�R�Q�O�P�X)�|(�Q�R�Q�O�P�X�{�Q�Q�Q�O�P�X�{�Q�P�Q�O�P�X�{�E�E�E�{�P�Q�O�P�X)}
�@�@�@���S�R�E�O���O�E�E�E�i���j
NO3�u�W���[�J�[�v
02/12 17��42���@��M �X�V 2/23






NO3�u�W���[�J�[�v
02/22 10��47���@��M �X�V 2/23





�F����A���⎿��ɓ����Ă��������B�ꕔ�ł��\���܂���A�ƃy���l�[����Y���āA���[���ő����Ă��������B�҂��Ă��܂��B
