令和６年３月３日

[流れ星]

　　第438回数学的な連続応募問題

　　　＜解答募集期間：３月３日〜３月３１日＞

「歴史上の定理］

問題１　

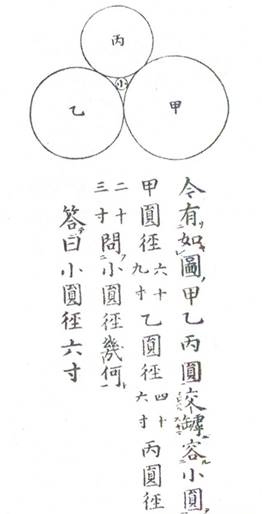
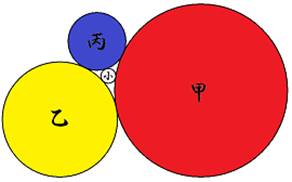互いに接する３個の甲乙丙の円径を六十九寸 , 四十六」寸 , 二十三寸とするとき,これらすべてに外接する小円の円径を求めよ。　

答曰　六寸

文献　算法点竄初學抄　橋本昌方著

原典　デカルトの円定理

注　ルネ・デカルトは1643年にボヘミヤのエリザベス女王への手紙の中でこの問題を詳細に研究している。

　この定理は江戸時代にはよく知らた定理で多くの算額の問題を解くのに使われていた。

問題２

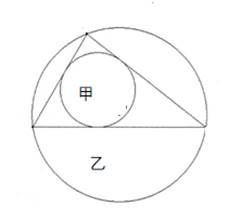三角形に内接する甲円と外接する乙円があり　甲の半径を四寸　乙円の半径を九寸とする。　

甲円乙円の中心間の距離を求めよ。

原典　オイラー・チャップル定理

次の２問は大学入試問題にもありそうな問題

問題３

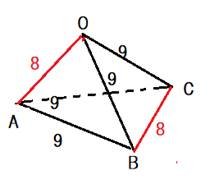
図のように三辺の長さが八、九、九である等面四面体ＯＡＢＣがある、次の値を求めよ。

（１）四面体ＯＡＢＣの体積

（２）四面体ＯＡＢＣ外接球の半径

（３）四面体ＯＡＢＣ内接球の半径

　

　

問題４

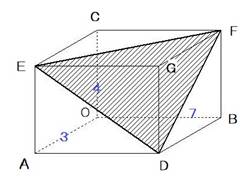
図のように三辺の長さが三、四、七である直方体の中に四面体ＤＥＦＧがある。

次の値を求めよ。

（１）四面体ＤＥＦＧの表面積

（２）四面体ＤＥＦＧの外接球の半径

（３）四面体ＤＥＦＧの内接球の半径

追加問題（出題者は「ジョーカー」）

　今回から2024に関する問題シリーズ第4段で終了

問題１

問題２

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。