令和７年１２月７日

[流れ星]

　　第462回数学的な連続応募問題

　　　＜解答募集期間：12月7日〜1月4日＞

［最短距離］

　

問題

文字はすべて正の数とする。

ｘ^２＋ｙ^２＋ｘｙ＝４９

ｙ^２＋ｚ^２＋ｙｚ＝６４

ｚ^２＋ｘ^２＋ｚｘ＝２５

ｘ,y,ｚが上の３式を満たすとき,ｘ＋ｙ＋ｚの値を求めよ。

＊解法に使う参考図　点Pをフェルマー点という。

　ただし、△ABCは鋭角三角形のときの図

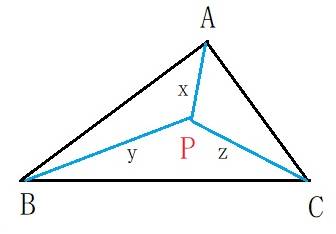
補題　鋭角三角形ＡＢＣにおいて,AB=c,BC=a,CA=b,面積をSとする。△ABCの内部に点Pをとり,AP＋BP+CPを最小にする点Pとする。このときのAP+BP+CPの値をa,b,c,Sで表せ。

追加問題（出題者は「ジョーカー」）　新作シリーズ

四分円内の正方形と正三角形の1辺について『３』　

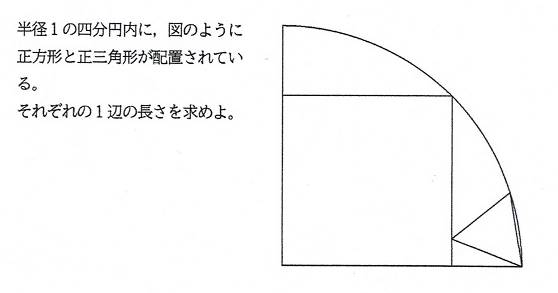
問題１　　シリーズ３問目

正方形と正三角形の1辺が異なる（ａ＞ｂ),

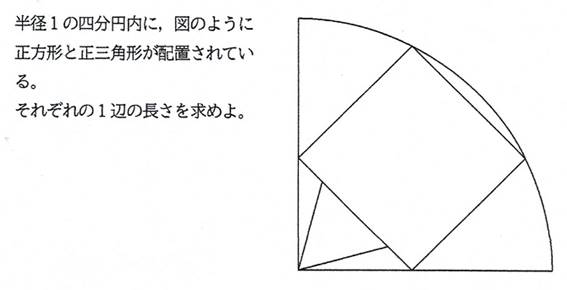
問題２　シリーズ４問目

正方形と正三角形の1辺が異なる（ａ＞ｂ),

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。