第144回数学的な応募問題[3本のくじ]
n個の整数1,2,3,・・・,nが書いてあるくじがあります.この中から3本のくじを引くとき,次のようなくじの引く方は何通りあるか.(ただし,n≧7とする)
問題1:3本のくじに書いてある数字のうち,どの2つの数の差も0以上となる場合.この場合は,くじを1本引いたあと,このくじを元に戻してください.
問題2:3本のくじに書いてある数字のうち,どの2つの数の差も1以上となる場合.
問題3:3本のくじに書いてある数字のうち,どの2つの数の差も2以上となる場合.
問題4:3本のくじに書いてある数字のうち,どの2つの数の差も3以上となる場合.
いつものようにコンピュータのプログラムで解いてみました.今回はグラフ作成ソフトGRAPESです.当然数学的には推論に穴がある解き方なのですが,数値解析という立場に立てば,何とか許されるでしょう.
n本のときのそれぞれの答をf(n)とする.
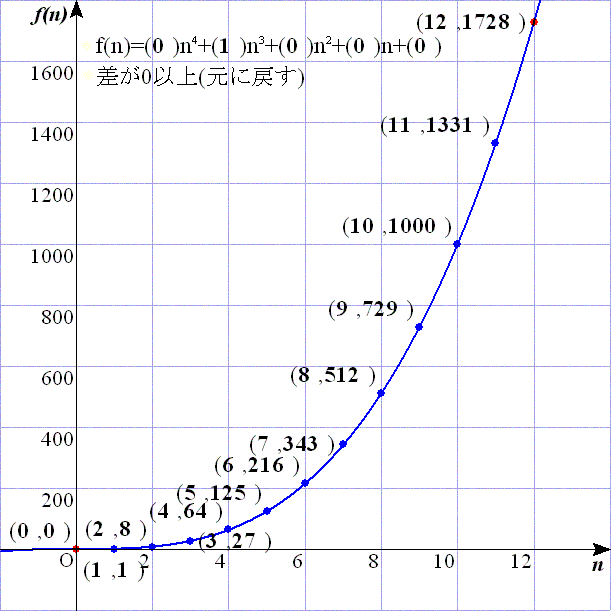
問題1:差(差の絶対値)が0以上になるのは必然なので,次のスクリプトでそれぞれのnの場合(1≦n≦12)のf(n)を計算した.
#
for a:=1 to n
# for b:=1 to n
# for c:=1 to n
# 答:=答+1
# draw
#
next c
# next b
# next
a
これにより,
f(1)=1,f(2)=8,f(3)=27,f(4)=64,f(5)=125,f(6)=216,f(7)=343,f(8)=512,f(9)=729,f(10)=1000,f(11)=1331,f(12)=1728
となるので,f(n)=n3となる.
関数式を求める際には,path関数(複数個の点を通る曲線のグラフを求める),cof関数(項の係数を求める)を使用している.
尚この場合n≧0で十分である.
スクリプト実行中のアニメは大変興味深いものがあった.
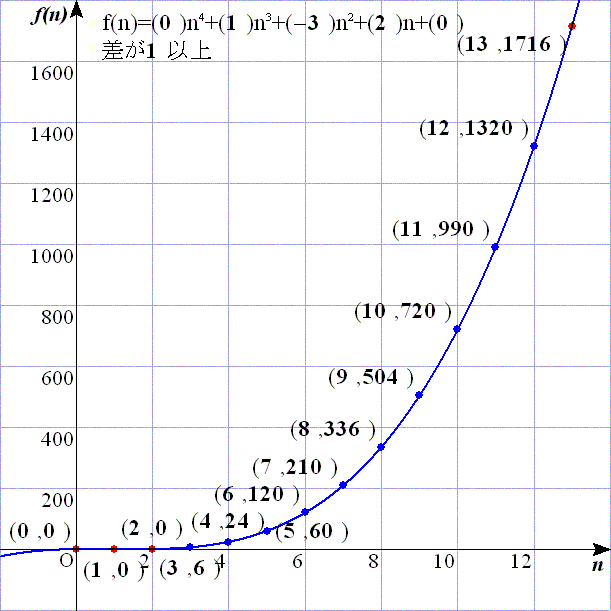
問題2:次のスクリプトでf(n)を計算した.取り出したくじは元に戻さないので,条件abs(a-b)>=sやabs(a-c)>=s,abs(b-c)>=s(s:=1)は必要ないのだが,これ以降の問題と同じスクリプトにする為に付けた.
#
s:=1
# for a:=1 to n
# for b:=1 to n
# if abs(a-b)>=s then
# for
c:=1 to n
# if abs(a-c)>=s and abs(b-c)>=s then
# 答:=答+1
#
draw
# endif
# next c
# endif
# next b
# next
a
これにより,
f(3)=6,f(4)=24,f(5)=60,f(6)=120,f(7)=210,f(8)=336,f(9)=504,f(10)=720,f(11)=990,f(12)=1320,f(13)=1716
となるので,f(n)=n3−3n2+2n=n(n−1)(n−2)となる.
尚この場合n≧0で十分である.
ちなみにこの答は,元に戻さずに差が0以上である場合の答にもなっている.
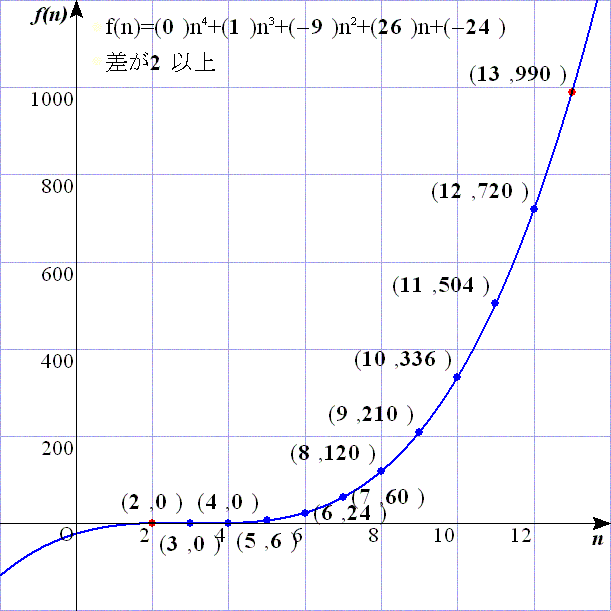
問題3:問題2と同様なスクリプトでf(n)を計算した.s:=2と変えただけである.これにより,
f(3)=0,f(4)=0,f(5)=6,f(6)=24,f(7)=60,f(8)=120,f(9)=210,f(10)=336,f(11)=504,f(12)=720,f(13)=990
となるので,f(n)=n3−9n2+26n−24=(n−2)(n−3)(n−4)となる.
尚この場合n≧2で十分である.
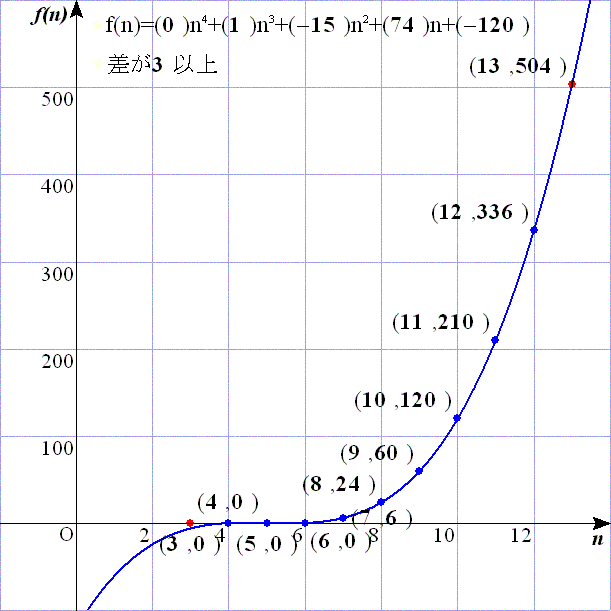
問題4:問題2のスクリプトでs:=3と変えただけである.これにより,
f(4)=0,f(5)=0,f(6)=0,f(7)=6,f(8)=24,f(9)=60,f(10)=120,f(11)=210,f(12)=336,f(13)=504
となるので,f(n)=n3−15n2+74n−120=(n−4)(n−5)(n−6)となる.
尚この場合n≧4で十分である.
さらに,差が4以上になる場合,s:=4として,
f(6)=0,f(7)=0,f(8)=0,f(9)=6,f(10)=24,f(11)=60,f(12)=120,f(13)=210,f(14)=336,f(15)=504
となるので,f(n)=n3−21n2+146n−336=(n−6)(n−7)(n−8)となる.
尚この場合n≧6で十分である.
差が5以上になる場合,s:=5として,
f(8)=0,f(9)=0,f(10)=0,f(11)=6,f(12)=24,f(13)=60,f(14)=120,f(15)=210
となるので,f(n)=n3−27n2+242n−720=(n−8)(n−9)(n−10)となる.
尚この場合n≧8で十分である.
以上の事から,差がs以上のとき(s≧1),
f(n)={n−(2s−2)}{n−(2s−1)}(n−2s)(n≧2s−2)
となる.
ちなみに4本のくじを引く場合は,
g(n)=n4−6n3+11n2−6n=n(n−1)(n−2)(n−3)(差が0以上,1以上,n≧0)
g(n)=n4−18n3+119n2−342n+360=(n−3)(n−4)(n−5)(n−6)(差が2以上,n≧3)
g(n)=n4−30n3+335n2−1650n+3024=(n−6)(n−7)(n−8)(n−9)(差が3以上,n≧6)
g(n)=n4−42n3+659n2−4578n+11880=(n−9)(n−10)(n−11)(n−12)(差が4以上,n≧9)
・・・
となるので,
g(n)={n−(3s−3)}{n−(3s−2)}{n−(3s−1)}(n−3s)(差がs以上,n≧3s−3)
となる.
蛇足の疑問なのですが,何故問題1で元に戻すようにしているのでしょうか.問題2以降と形をそろえる意味で,戻さないようにしてもよかったのでは.その方が場合分けが面倒くさくはなるのですが,興味深い問題になったかも知れません.
またnの条件も,場合の数を正の数にするという観点に立てばn≧7でよいのですが,問題4までではn≧4でも十分です.
毎回応募している訳でもないのに,厚かましい事を書いて申し訳ありません.