第１４４回数学的な応募問題［３本のくじ］
　答を_ｎ＋２Ｃ_３（＝_ｎＨ_３），_ｎＣ_３（＝_ｎ−２Ｈ_３），_ｎ−２Ｃ_３（＝_ｎ−４Ｈ_３），_ｎ−４Ｃ_３（＝_ｎ−６Ｈ_３）となるようにするのであれば，

　ｎ個の整数１、２、３、・・・、ｎが書いてあるくじがそれぞれ沢山あり、区別がつかないとします。この中から同時に３本のくじを引くとき、次のようなくじの引き方は何通りありますか。ただし、ｎ≧７とします。
問題１：３本のくじに書いてある数字のうち、どの２つの数の差も０以上となる場合。
問題２：３本のくじに書いてある数字のうち、どの２つの数の差も１以上となる場合。
問題３：３本のくじに書いてある数字のうち、どの２つの数の差も２以上となる場合。
問題４：３本のくじに書いてある数字のうち、どの２つの数の差も３以上となる場合。

とすればよいのではないでしょうか．
　解いてみます．
　ｎ本のときのそれぞれの答をｆ(ｎ)とし，差をｓ以上とする．
問題１：ｓ＝０であるから，GRAPESのスクリプトは
# s:=0
# for a:=1 to n
# for b:=a+s to n
# for c:=b+s to n
# 答:=答+1
# draw
# next c
# next b
# next a
　これにより，
　　f(1)=1,f(2)=4,f(3)=10,f(4)=20,f(5)=35,f(6)=56,f(7)=84,f(8)=120,f(9)=165,f(10)=220,f(11)=286,f(12)=364
となるので，ｆ(ｎ)＝ｎ^３／６＋ｎ^２／２＋ｎ／３＝ｎ(ｎ＋１)(ｎ＋２)／６＝_ｎ＋２Ｃ_３＝_ｎＨ_３となる．
　関数式を求める際には，path関数（複数個の点を通る曲線のグラフを求める），cof関数（項の係数を求める）を使用している．
　尚この場合ｎ≧０で十分である．
　スクリプト実行中のアニメは大変興味深いものがあった．


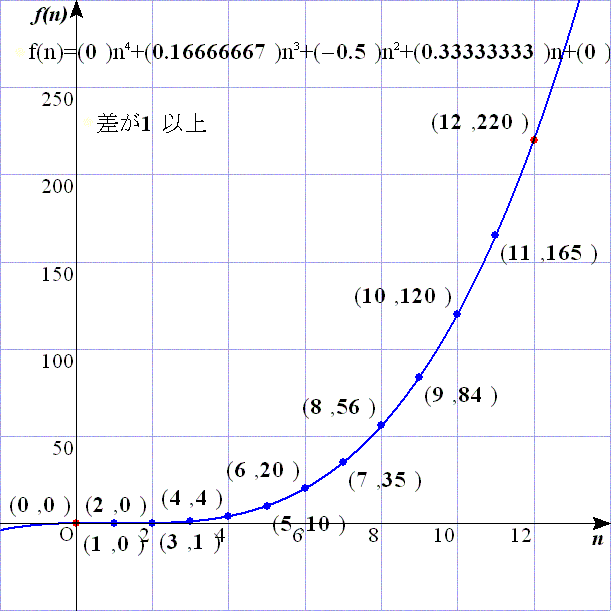
問題２：問題１のスクリプトでs:=1とするだけである．
　これにより，
　　f(0)=0,f(1)=0,f(2)=0,f(3)=1,f(4)=4,f(5)=10,f(6)=20,f(7)=35,f(8)=56,f(9)=84,f(10)=120,f(11)=165,f(12)=220
となるので，ｆ(ｎ)＝ｎ^３／６−ｎ^２／２＋ｎ／３＝ｎ(ｎ−１)(ｎ−２)／６＝_ｎＣ_３＝_ｎ−２Ｈ_３となる．
　尚この場合ｎ≧０で十分である．


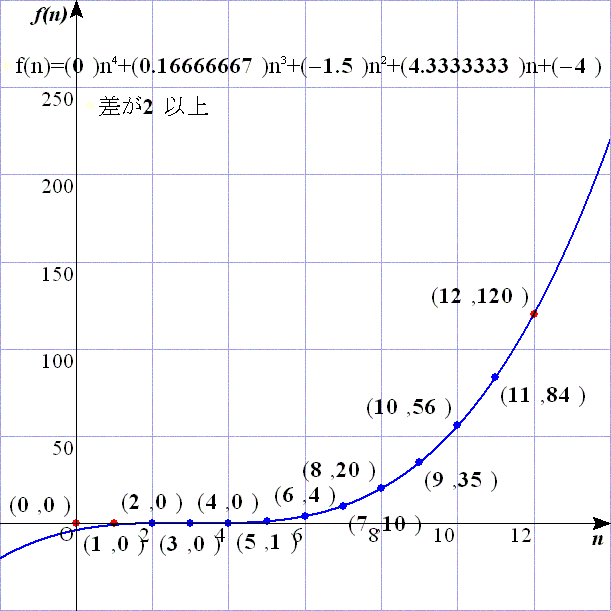
問題３：問題１のスクリプトでs:=2とするだけである．
　これにより，
　　f(2)=0,f(3)=0,f(4)=0,f(5)=1,f(6)=4,f(7)=10,f(8)=20,f(9)=35,f(10)=56,f(11)=84,f(12)=120
となるので，ｆ(ｎ)＝ｎ^３／６−３ｎ^２／２＋１３ｎ／３−４＝(ｎ−２)(ｎ−３)(ｎ−４)／６＝_ｎ−２Ｃ_３＝_ｎ−４Ｈ_３となる．
　尚この場合ｎ≧２で十分である．


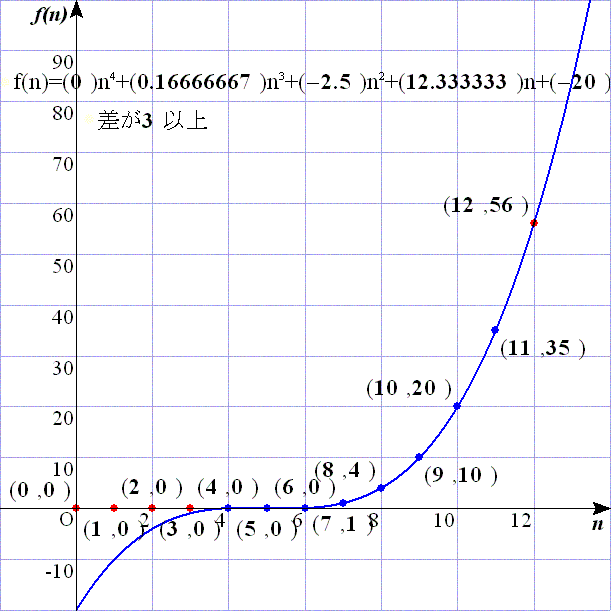
問題４：問題１のスクリプトでs:=3とするだけである．
　これにより，
　　f(4)=0,f(5)=0,f(6)=0,f(7)=1,f(8)=4,f(9)=10,f(10)=20,f(11)=35,f(12)=56
となるので，ｆ(ｎ)＝ｎ^３／６−５ｎ^２／２＋３７ｎ／３−２０＝(ｎ−４)(ｎ−５)(ｎ−６)／６＝_ｎ−４Ｃ_３＝_ｎ−６Ｈ_３となる．
　尚この場合ｎ≧４で十分である．


　さらに差が４以上の場合，s:=4とすればよく，
　　f(6)=0,f(7)=0,f(8)=0,f(9)=1,f(10)=4,f(11)=10,f(12)=20
となるので，ｆ(ｎ)＝ｎ^３／６−７ｎ^２／２＋７３ｎ／３−５６＝(ｎ−６)(ｎ−７)(ｎ−８)／６＝_ｎ−６Ｃ_３＝_ｎ−８Ｈ_３（ｎ≧６）となる．

　差が５以上の場合，s:=5とすればよく，
　　f(8)=0,f(9)=0,f(10)=0,f(11)=1,f(12)=4
となるので，ｆ(ｎ)＝ｎ^３／６−９ｎ^２／２＋１２１ｎ／３−１２０＝(ｎ−８)(ｎ−９)(ｎ−１０)／６＝_ｎ−８Ｃ_３＝_ｎ−１０Ｈ_３（ｎ≧８）となる．

　以上の事から，差がｓ以上のとき（ｓ≧１），
　　_ｎ−２ｓＨ_３＝_{ｎ−２ｓ＋２}Ｃ_３（ｎ≧２ｓ−２）
となる．