平成15年3月31日
 [流れ星]
[流れ星]
第116回数学的な応募問題解答
<解答募集期間:3月16日〜3月31日>
[絵画鑑賞]
太郎さんは、以前次のような入試問題を生徒と一緒に考えました。
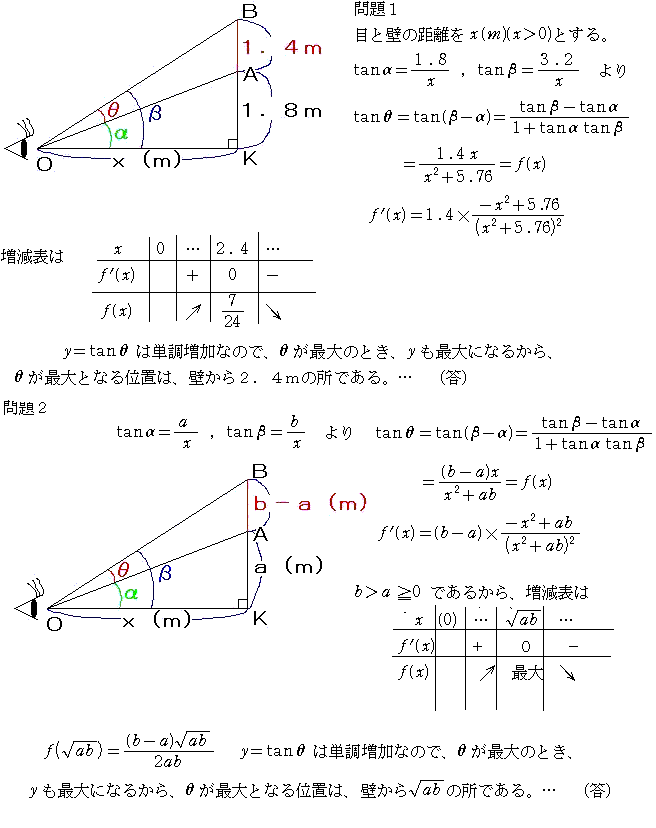
問題1.縦1.4mの絵が垂直な壁に掛かっていて、絵の下端が目の高さより1.8m上方の位置にある。
この絵を、縦方向に見込む角が最大となる位置は、壁から何mの所か。
求められた答えが一体どんな数字か知りたくて、文字に置き換えて考えました。
問題2.縦(b−a)mの絵が垂直な壁に掛かっていて、絵の下端が目の高さよりam上方の位置にある。
この絵を、縦方向に見込む角が最大となる位置は、壁から何mの所か。
ただし、bはaより大きい数とする。また、参考に下のような画像を作ってあります。

NO1「H7K」さん 3/15: 12時49分 受信 更新3/31

NO2「午年のうりぼう」さん3/16:03時04分 受信更新3/31
NO3「Kashiwagi」さん
3/16: 18時28分 受信 更新3/31
お世話になります。今回の問題は問2の図で助かりました。問2の一般解を求め具体値を代入して問1を求めました。
しかし、面白い結果になるのですね。何かレンズや鏡の関係と似ていますね。
第116回解答
今回の問題は問2が一般解なのでこちらを先に解き、その解に具体的な値を代入し、問1の解とする。
問2.
図のKOをxとすると、tanα=a/x,tanβ=b/x
又、tanθ=tan(β−α)=(tanβ−tanα)/(1+tanα・tanβ) =(b−a)x/(x2+ab)となる。
ここで見込む角が最大になるとは、角βが最大になることであり、αは定角であるからθを最大にすれば良い。題意よりθは0°と90°の範囲にある。
そこで先程のxの関数であるtanθ式をxで微分すると、
〔(b−a)(x2+ab)−2x(b−a)x〕/(x2+ab)2
分子を整理すると−(b−a)(x2−ab)=−(b−a)(x+√ab)(x−√ab)となる。
そこで増減を確認すると、x=√abで極大値をとることがわかり、この値が最大値でもある。以上より求めるものは壁から√abmである。
問1.
問2の解にa= 1.8m、b=1.4+a=3.2mを代入して2.4mが求めるものである。
NO4「午年のうりぼう」さん別解3/17:23時37分受信更新3/31
NO5「toru」さん
3/18: 11時57分 受信 更新3/31
問題2
解答1 0<θ<π/2 であるから、tanθはこの範囲で単調増加であり、tanθが最大と
なる点を求めればよい。OK=xとすると、tanθ=tan(β-α)=(tanβ-tanα)/(1+tan
αtanβ)=(b/x-a/x)/(1+(ab)/(x^2))=(b-a)/(x+(ab/x))≦(b-a)/2√(x・(ab/x))
=(b-a)/2√(ab) 等号はx=ab/xの時に成り立つからこの時、x=√(ab) (m) 答え
解答2 ABの中点をM、3点O,A,Bを通る円の中心をPとするとPM⊥AB、円周角と中心
角の関係から、角APB=2×角AOBだから、角APBが最大になるように考えればよい。
このためにはこの円の半径rが最小となればよいが、これは円がOKに接する時で、PO
⊥OKとなるから、r=PO=MK=(b+a)/2 この時、OK^2=PM^2=PA^2−AM^2=((b+a)/2)^2
−((b-a)/2)^2=ab でOK=√(ab)
(m)答え
問題1 a=1.8 b=3.2 とすれば√(1.8×3.2)=2.4(m) 答え
解答1ではなんとなく計算して行けばできてしまうので、ふつうはこちらだと思いますが、解答2の方が個人的には好きです。
NO6「浜田」さん 3/18: 12時21分 受信 更新3/31
問題2.
OK=x(x>0)とする.
θ=β−α
tanα=a/x
tanβ=b/x
であるから,
tanθ=tan(β−α)
=(tanβ−tanα)/(1+tanαtanβ)
=(b/x−a/x)/(1+a/x×b/x)
=(b−a)×x/(x^2+ab)
tanθ(0<θ<π/2)は増加関数であり,b−a>0であるから,θが最大となるのは,tanθが最大,すなわち
f(x)=x/(x^2+ab)
が最大になるときである.
f'(x)={(x^2+ab)−x×2x}/(x^2+ab)^2
=−(x^2−ab)/(x^2+ab)^2
ab>0であるから,増減表は,
x 0 … (ab)^(1/2) …
f'(x) + 0 −
f(x) / \
故にx=(ab)^(1/2)のとき最大となる.
答.(ab)^(1/2)m
問題1.
問題2において,a=1.8,b=1.4+1.8=3.2とすればよいので,
OK=(1.8×3.2)^(1/2)=2.4
答.2.4m
NO7「UnderBird」さん 3/18:
13時20分 受信 更新3/31

NO8「浜田」さん別解 3/19: 14時25分 受信 更新3/31

NO9「UnderBird」さん別解3/24:
10時25分受信 更新3/31


No10「中川幸一」さん 3/26: 01時36分 受信 更新3/31

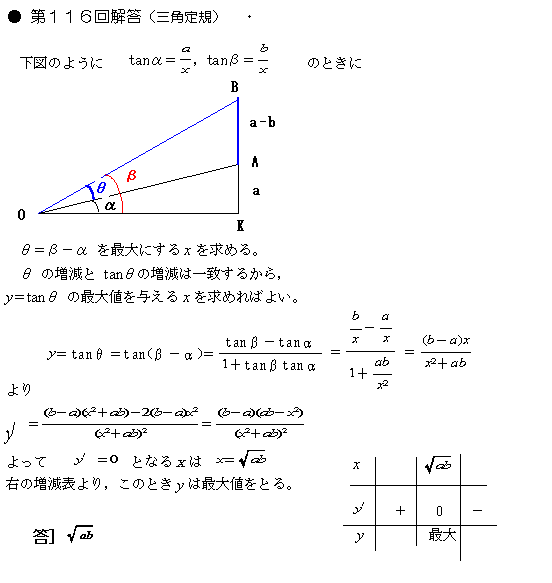
NO11「三角定規」さん 3/29: 20時57分 受信 更新3/31
![]()
