平成15年7月27日
 [流れ星]
[流れ星]
第122回数学的な応募問題解答NO2
<解答募集期間:7月6日〜7月27日>
[増えた1cm2]
太郎さんは、月曜日第7限の「総合的な学習の時間」に1年生を対象にして、「楽しい数学」と称した講座を受け持っています。現在は「フィボナッチ数列」の調べ学習をしています。この中で、次のような課題を生徒に伝えています。
皆さんも、考えて、増えた1cm2 はどうしてか 考えてください。
参考:{an}:{1,1,2,3,5,8,13,21,34,55,89,・・・}をフィボナッチ数列という。
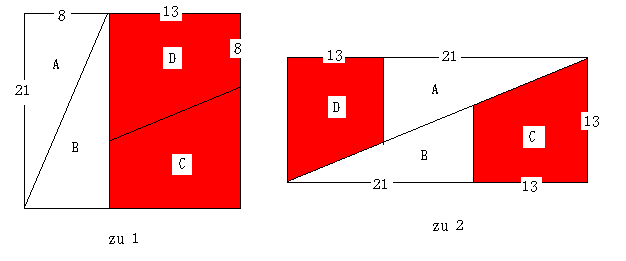
問題:最初 1辺が21cmの正方形を下の図のように4つの部分に分けました。三角形Aと三角形Bは合同、
三角形Cと三角形Dは合同です。次に、この4つを移動させて、[zu2]の図形を作りました。
見た目は長方形ですから、面積を考えてみると、横13cm、縦(13+21)cmになります。
4つの部分を移動しただけですから、面積は同じになるはずです。どうして、1cm2違うのでしょうか。
この違いは、「フィボナッチ数列」にどんな性質があるからでしょうか。
NO7「中川幸一」さん 7/26: 23時48分 受信 更新7月27日
今回も大変ギリギリでスミマセン。
一応解答は一般化しておきました。
今回はFibonacci数列の有名な性質の問題でしたね。
今回も大変面白い問題でした。

NO8「午年のなりぼう」さん 7/27: 01時10分 受信 更新7月27日
第122回数学的な応募問題 [増えた1cm2]
(解答)


![]()
