�����P�T�N�P�P���P�U��
 [���ꐯ]
[���ꐯ]
�@�@�@�@�@�@�@�@��P�Q�V�����w�I�ȉ������
�@�@�@�@�@�@�@�@�@�@����W���ԁF�P�O���Q�U���`�P�P���P�U����
�m�Ԑڏؖ��n
�@�@�@
������k�ɁA�u�Ԑڏؖ��Ƃ��āA�w���@�A��ɂ��ؖ��A����@�����邪�A���̃��[���X�E�V���^�C�i�[���Ƀ`�������W���Ă݂Ȃ����v
�ƌ����܂����B�����ŁA���ʊ̖��ł��B�������A���ڏؖ��ł��Ԑڏؖ��ł������܂�����ˁB
�O�p�`�`�a�b�ɂ����āA�a�b�����C�b�`�����C�`�a�����Ƃ���B�`�a�A�`�b��ɓ_�c�A�d���p�b�C�p�a���Q��������悤�ɂƂ�B
�@�@�a�d���b�c�Ȃ�`�a���`�b�@���������邱�Ƃ��ؖ�����B
�m�n�P�u����K��v���� 10/26: 06��24�� ��M �X�V11/16

�m�n�Q�ukasama�v 10/28: 23��4�P�� ��M �X�V11/16
���R�����g�������y���������o�肵�Ē������肪�Ƃ��������܂����B�d������i�������̂ŁA���Ɏ��g��ł݂܂����B
�@�ȒP�Ɍ������̂ŁA�����Ԗ�����̂܂܂ł����B�������A���w�E�̂悤�ɂ���Ă݂�ƈӊO�Ƌ�J���܂����B
�u���ڏؖ��v�Ɓu�Ԑڏؖ��v�̂Q����낤�Ǝv�����̂ł����A�ƂĂ�����ȗ]�T�͂���܂���ł����B
�@�����̂Ƃ���́A�u���ڏؖ��v�����ƂȂ��Ă��܂��܂����B�ŁA�u���ڏؖ��v�̉�������v���܂����A�قƂ�Ǘ͋Z�ł�����悤�Ȃ��̂ŁA
�����\�t�g�̂����ɂȂ�܂����B
�@���ꂩ��A�Ԑڏؖ����l���Ă݂܂����A���܂����ƒ��ڏؖ����X�}�[�g�ɂł������Ɏv���܂����E�E�E
�y���ڏؖ��z
�@AE�ACE�AAD�ABD�̒������Z�o
�y�⑫�P�z���A AE=bc/(a+c)�ACE=ab/(a+c)�@ AD=bc/(a+b)�ABD=ac/(a+b)
�A��BE�ACD�Ƒ��ӂ̒����W
�y�⑫�Q�z�Ƈ@���A�@
BE2=ac-AE�CE
=ac-ab2c/(a+c)2
=(ac(a+c)2-ab2c)/(a+c)2
=ac{(a+c)2-b2}/(a+c)2
=ac(a+c-b)(a+c+b)/(a+c)2���(1)
���l�ɁACD�ɂ��Ă�
CD2=ab(a+b-c)(a+b+c)/(a+b)2���(2)
�ƂȂ�܂��B
�BBE=CD��AB=AC�̏ؖ�
���āABE=CD��BE2-CD2=0�ł�����A�A��(1)�A(2)����������ƁA
BE2-CD2=ac(a+c-b)(a+c+b)/(a+c)2-ab(a+b-c)(a+b+c)/(a+b)2=0
���@(a+b)2ac(a+c-b)(a+c+b)-(a+c)2ab(a+b-c)(a+b+c)=0
���@a(a+c+b){(a+b)2c(a+c-b)-(a+c)2b(a+b-c)}=0
�����ŁAa(a+c+b)>0�ł�����A
(a+b)2c(a+c-b)-(a+c)2b(a+b-c)=0
�ɂ��čl���܂��B��͘r�͂�(�ƌ����Ă��A�f��ł��̂͑�ςȂ̂ŁAMathmedia�̗͂����)�A�㎮��W�J����ƁA
-a3b-a2b2+a3c-3ab2c-b3c+a2c2+3abc2+bc3=0�@�ƂȂ�Ac-b�Ŋ��肾����
(c-b){a3+a2b+(a2
+ 3ab + b2)c + bc2}=0�@�ƂȂ�܂��B������{}�̒��͐��Ȃ̂��@ c-b=0�@���@c=b
�ł��B�ȏ���ABE=CD�Ȃ�AB=AC�ƂȂ�܂��B
�y�Ԑڏؖ�(2003.11.10�lj�)�z
BE=CD��AB=AC�̑���Ƃ��āAAB��AC��BE��CD�̏ؖ��ɒ��킵�Ă݂܂����B�y���ڏؖ��z�̇B���t���ɒH���Ė����������Ηǂ��̂ł����A�ʂ̊ϓ_����l���Ă݂܂����B�Ԑڏؖ��͒��ڏƖ�����̂�����ȏꍇ�ɗ��p�����̂ł����A�ȉ��ɏq�ׂ���̂͂��ƂĂ��ʓ|�������̂ŁA�{���̎�|�ɔ����Ă���ł��傤�B�����́A��BCE�Ƈ�BCD�ɐ����藝��K�p���āABE-CD���l��AB��AC�i��B����C�j��BE-CD��0���܂��B���j�͗��̂ł����A���ۂɂ���Ă݂�ƁA���ꂪ�Ȃ��Ȃ����܂��������A���s������J��Ԃ��āA�O�p���̕ό`�Ɗi������H�ڂɂȂ�܂����B
�@�����藝�̓K�p
��B = 2���A��C
=2���Ƃ��܂��BAB��AC�Ȃ̂��������ł����A�������Ƃ��Ă����܂��B
����ƁA��BCE�ɐ����藝�̓K�p���āA
a/sin{2��-(��+2��)} =
BE/sin(2��)
��1/BE = -sin(�� +
2��)/a�sin(2��) ��� (1)
���l�ɁA��BCD�ɂ��Ă�
a/sin{2��-(2��+��)} =
CD/sin(2��)
��1/CD = -sin(2�� +
��)/a�sin(2��) ��� (2)
�ł��B�Ȃ��Asin(2��)��0�Asin(2��)��0�ł��B
�A�ؖ��̏���
BE��CD�͋t���ɂ��Ĉ��Z����ƁA(1)�A(2)�����
1/BE - 1/CD
= - sin(�� + 2��)/a�sin(2��)
+ sin(2�� + ��)/a�sin(2��)
= {sin(2�� + ��)�sin(2*��) - sin(2��)�sin(��
+ 2��)} / a�sin(2��)�sin(2��)
1/BE - 1/CD��0�������Ηǂ��̂ŁA{}�̒������ɒ��ڂ��܂��B�a�E���̐ς̕ϊ������̂P�ł���
sin(��)�sin(��)=-{cos(��+��)-cos(��-��)}
/ 2
�𗘗p����ƁA{}��
�@{}
= -{cos(2��+3��)-cos(2��-��)}/2
+ {cos(3��+2��)-cos(��-2��)} / 2
�ƂȂ�A������ύX���Đ�������ƁA
�@{}
= {cos(3��+2��)-cos(2��+3��) + cos(2��-��)-cos(��-2��)} / 2
����ɁA�莮��{}�̒�������Ώۂɂ��܂��B�ĂсA�ʂ̘a�E���̐ς̕ϊ������ł���
cos(��)-cos(��) = -2�sin{(��+��)/2}�sin{(��-��)/2}
�𗘗p����ƁA{}��
�@{}
= -2�sin{5(��+��)/2}�sin{(��-��)/2} - 2�sin{3(��-��)/2}�sin{(��+��)/2}
�@�@
= -2�[sin{5(��+��)/2}�sin{(��-��)/2} + sin{3(��-��)/2}�sin{(��+��)/2}]
�܂��A[]�̒������l���āA
(��+��)/2=A�A(��-��)/2=B ��� (3)
�Ƃ���ƁA
[] = sin(5A)�sin(B)
+ sin(3B)�sin(A) ��� (4)
�ƂȂ�܂��B���\�_���_���Ǝ���ό`���܂������A����ŏ��������ł���܂��B�������̂Ƃ��A�㎮(4)�܂�BE��CD����0�łȂ����Ƃ��ؖ����܂��B
�B��������BE-CD�̏ؖ�
�O�p�`�̐�������A0��2����2����2�A0��2��+2����2�Ȃ̂ŁA(3)����A�AB�̂Ƃ蓾��͈͂�
�@0��A����/4�A-��/4��B����/4
�ł��̂ŁA
�@0��sin(A)��1/��2�A-1/��2��sin(B)��1/��2
��� (5)
�ł��B����(4)����W�J�i3�5�{�p�̌������p�j����Ɓi�{���͎�ł��̂̓`���b�g����Ȃ̂ŁA�����\�t�g���p���āj�A
�@(4)��
= -20�sin3(A)�sin(B)-4�sin3(B)�sin(A)+8�sin(A)�sin(B)+16�sin5(A)�sin(B)
�ƂȂ�悤�ł��B4�sin(A)�sin(B)�Ŋ���o���Đ��������
�@(4)��
= 4�sin(A)�sin(B)�{4�sin4(A)-5�sin2(A)-sin2(B)+2}
�����ŁAsin(A)�sin(B)��0������A�܂��܂��A{}�̒������l���āA�͈�(5)���ӎ����Ȃ��琮������ƁA
�@{}
= 4�[sin2(A)-1/2]2 + 4�sin2(A)-1 -5�sin2(A)-sin2(B)+2
= 4�[sin2(A)-1/2]2
- sin2(A) - sin2(B) + 1
= 4�[sin2(A)-1/2]2
+ [1/2-sin2(A)] + [1/2-sin2(B)]
�ƂȂ�A[]2��[]�͐��Ȃ̂ŁA{}���O�ł��B�܂�A��������BE-CD��0�ł��B����āAAB��AC��BE��CD�ł��B
�Q�l�܂łɁA4�sin4(A)-5�sin2(A)-sin2(B)+2�͉��}�̂悤�ȊO�ςł��B���́A�܂������`�悵�āA4�sin4(A)-5�sin2(A)-sin2(B)+2��0���傫�����낤�Ƃ���������܂����B
�@�@�@�@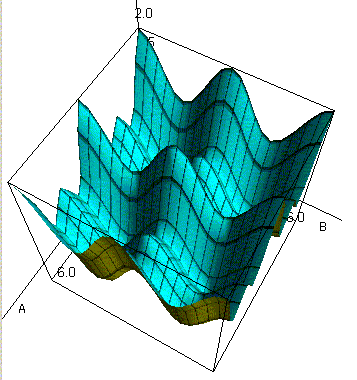
�m�n�Q�ukasama�v 10/28: 23��4�P�� ��M �X�V11/16�@����
�y�⑫�P�z
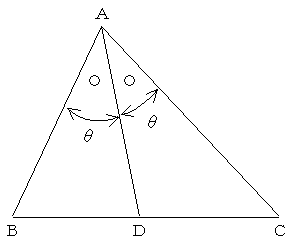
��ABC�ɂ����āA��A�̂Q��������BC�Ƃ̌�_��D�Ƃ���ƁABD:DC��AB:AC�ł��B
�ŋ߂̒��w���͂��̒藝��m���Ă���݂����ł���(���l���E�X�̒藝�Ȃ��m���Ă���悤�ł��B���͒��w�Z�ŏK�����L���͂Ȃ��̂ł�������P�Ɏ��Ƃ��Ă��Ȃ��������������H)�B�Ȃ̂ŁA�قƂ�NJ��������ɋ߂��ł����A�Q�l�܂łɏؖ����L�ڂ��Ă����܂��B
�y�ؖ��z�@���`=2���Ƃ���ƁA
2�~��ABD=AB�AD�sin���A2�~��ADC=AC�AD�sin���ł��B
����A2�̎O�p�`�̍����͓������ł�����A
��ABD:��ADC=BD:DC�@�ł��B�܂�A
BD:DC=AB�AD�sin��/2:AC�AD�sin��/2=AB:AC�@�ƂȂ�܂��B
�y�⑫�Q�z��}�ɂ����āA AD2=AB�AC-BD�DC�@�ł��B
�y�ؖ��z�@��ABD�A��ADC�ɗ]���藝��K�p���܂��B����ƁA
BD2=AB2+AD2-2�AB�AD�cos��
CD2=AD2+AC2-2�AD�AC�cos���@�ł��B�����ό`����
�@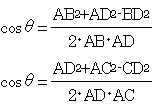
�Ƃ���āAcos�������������
AC�(AB2+AD2-BD2)=AB�(AD2+AC2-CD2)
���@AD2�(AC-AB)= AB�AC2-AB�CD2-AC�AB2+AC�BD2
���@AD2�(AC-AB)= AB�AC�(AC-AB)-AB�CD2+AC�BD2
�ƂȂ�܂����AAB�CD2+AC�BD2�̕����͕⑫�P�ɋL�ڂ����悤��
BD:DC=
AB:AC�@���@BD�AC=DC�AB
���@DC2�AB��BD�AC�DC�AAC�BD2=DC�AB�BD�@�ł�����A
AD2�(AC-AB)= AB�AC�(AC-AB)-BD�DC�(AC-AB)
�Ɛ����ł��܂��B
�@AC��AB�̏ꍇ
���ӂ���AC-AB���͂���āAAD2= AB�AC-BD�DC�ƂȂ�܂��B
�AAC��AB�̏ꍇ
BD=CD�A��ADB=��ADC=��/2�ŎO�����̒藝����
AD2=
AB2-BD2
�m�n�R�uKashiwagi�v10/30: 7��50��
��M
�m�n�R�uKashiwagi�v11/01: 22��20�� ��M
�m�n�R�uKashiwagi�v11/02: 12��29�� ��M �X�V11/16
��12�V��
�y���ڏؖ��z.
��ӂ��AB�AAC�ABE�y��CD�̒������e�X���A���A���A���Ƃ���ƁA�p�̓��̐������AE�������^�i���{���j�C�`�c�������^�i���{���j�ƂȂ�B
�����Ł�ABC�Ɓ�ABE�ɗ]�����藝��K�p�����
a�Q�����Q�{���Q�|�Q����cosA�@�@�@�@�c�E�@�@
���Q�����Q�{���Q���Q�^�i���{���j�Q�|�Q�����QcosA�^�i���{���j�@�c�E�@�A�ƂȂ�B
�@�y�чA����cosA�@�����������
���Q�����Q�{���Q���Q�^�i���{���j�Q�|�ia�Q���|���Q���|���R�j�^�i���{���j�@�c�E�B��B
�S�����l�Ȏ��� ��ABC�Ɓ�ACD�ɓK�p�����
���Q�����Q�{���Q���Q�^�i���{���j�Q�|�ia�Q���|���R�|�����Q�j�^�i���{���j�c�E�C�ƂȂ�B
������BE��CD�ł��邩�炘���������A���Q�����Q�ł��邩��A
�B�y�чC���@���Q�{���Q���Q�^�i���{���j�Q�|�ia�Q���|���Q���|���R�j�^�i���{���j
�����Q�{���Q���Q�^�i���{���j�Q�|�ia�Q���|���R�|�����Q�j�^�i���{���j�ƂȂ�B
���̎����v�Z����ƁA
�i���|���j�k���Q���{���i���{���j�Q�{a�Q�i���{���j�{abc�l���O�ƂȂ�B
�Ƃ���ŁA���A���A���͊e�X���̐��ł��邩��k�l�Ȃ��͐��A�����O�łȂ��B
�����āA���|�����O�����藧���A�������@�����AAB��AC�ł���B
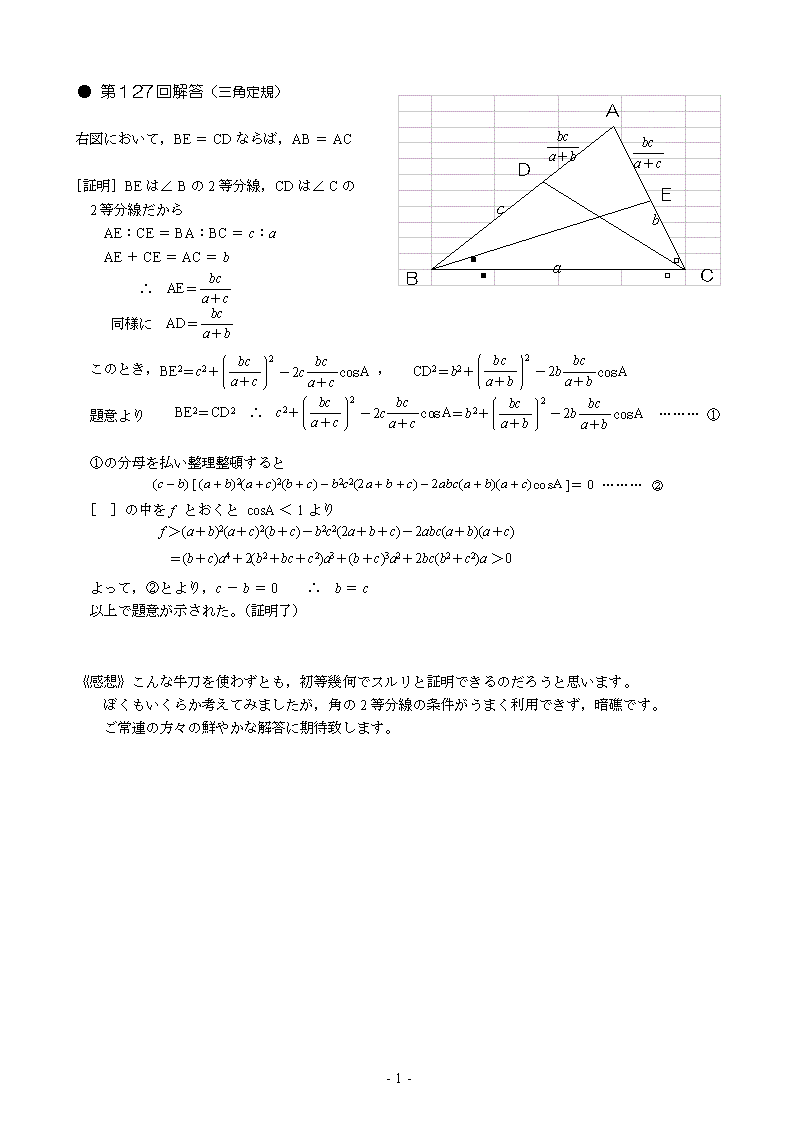
�y�ԐڏƖ��z
�Ⴆ��A���R�O���A��C���X�O���AAB���Q�AAC=��R�ABC���P�̒��p�O�p�`���l����ƁAA�a��AC�ł���B
���ABE=x�ACD�����Ƃ���ƁA���d�a�b�́ڂd�a�b���R�O���̒��p�O�p�`�ł��邩��
�����Q��R�^�R�ƂȂ�B
���A�c���ӂa�b�ɕ��s�����cF�������ƁA�cF��F�b�����^��Q�ł���B
�����āA���`�c�d�́ڂ`���R�O���̒��p�O�p�`�ł��邩��A�����i�R��Q�|��U�j�^�Q
�ƂȂ�B�����A�������A�a�d��C�c�ƂȂ�B
�܂�AA�a��AC�Ȃ�Ίe�X�̊p�̓����ł���a�d��C�c�̊Ԃɂ͂a�d��C�c�����藧�B
����͑�ӂ̑������鎖���Ӗ�����B
�����āA�a�d���b�c�Ȃ�`�a���b�c����������B
�m�n�S�utoru�v 10/30: 11��52�� ��M �X�V11/16
��P�Q�V���
���ږ@�@AE=bc/(a+c)�A��ABE�ɗ]���藝��K�p���āA
BE^2=c^2+b^2c^2/(a+c)^2-2bc^2/(a+c)
cos A
��ABC�ɗ]���藝��K�p����cosA=(b^2+c^2-a^2)/2bc����̎��ɑ�����Čv�Z�A
BE^2=c^2+b^2c^2/(a+c)^2-2bc^2/(a+c) cos A=ac((a+c)^2-b^2)/(a+c)^2
b��c�����ւ���@CD^2= ab((a+b)^2-c^2)/(a+b)^2
BE^2=CD^2�Ƃ����
ac((a+c)^2-b^2) (a+b)^2= ab((a+b)^2-c^2) (a+c)^2 ���ӂ�a�Ŋ����Đ�������ƁA
(b-c) (a+c)^2(a+b)^2+bc(b(a+b)^2-c(a+c)^2)=0�@�����
(b-c) ((a+c)^2(a+b)^2+bc(a^2+2a(b+c)+b^2+bc+c^2))=0 �A2�Ԗڂ̃J�b�R���͐���
���邩��Ab-c=0 �ł`�a���`�b
�@
�Ԑږ@�@�`�a���`�b�Ȃ�a�d���b�c�������B
�b��ʂ�a�d�ƕ��s�Ȓ������Ђ��A�`�a�̉����Ƃ̌�_���e�Ƃ���ƁA�p�a�b�e���p
�a�e�b���p�a�^�Q���a�e��a�A���`�a�d�ƃ��`�e�b�̑�������
�a�d��c/(a+c)�~�b�e�@
���l��B��ʂ�b�c�ɕ��s�Ȓ����������`�b�̉����Ƃ̌�_���f�Ƃ���Ƃb�f��a��
�b�c��b/(a+b)�~�a�f�@
�`�a���`�b�̎��A�p�a���p�b�ŁA�p�e�a�b���p�f�b�a������ӎO�p�`�A���a�e�b
�ƃ��b�f�a���ׂāA�b�e���a�f---1)�@
�܂�c��b��a/c��a/b��(a+c)/c��(a+b)/b��c/(a+c)��b/(a+b)--2)
1)2)��ӕӂ�����A�a�d���b�c
�`�a���`�b�Ȃ瓯�l�ɂa�d���b�c�ƂȂ邩��A�`�a���`�b�Ȃ�a�d���b�c�͎�����
���B
����������Ƃ��܂����@�����肻���ȋC�����A�Ȃ��Ȃ����܂������܂���ł����B
�m�n�T�uH7K�v 10/30: 21��59�� ��M
�m�n�T�uH7K�v
11/02: 22��19�� ��M
�m�n�T�uH7K�v
11/04: 22��44�� ��M �X�V11/16
�L���}��Fang:�� in:�� //:���s�L��
D' : DD'//BC,D' in AC.
E' : EE'//BC,E' in AB.
����ƁC���s���̍��p���ang D'DC=ang
DCB=ang DCA�C�����DD'=CD'�C���l��EE'=BE'�D
���āCDD'��EE'������ɗ���Ɖ���D
������C���炩��DD'<EE'�C�܂�DD'��EE'������ɂ��邽�߂ɂ�
BE sin ang EBC= BE in ang
ABE<CD sin ang DCB=CD sin ang
DCA���K�v�C
�����0<ang DCA�@,�@ang
ABE<90�����ang DCA>ang
ABE�D
���ɁA CD =2DD'cos ang DCA= BE=2EE'cos ang ABE�C
�i�ȉ��ؖ��F�@DD'//BC���ang D'DC=ang
DCB=ang DCA�C�����DD'=D'C�D
�@�����ŁC��DD'C�ɂ���D'����CD�ɐ��������낷�i����R�Ƃ���j�ƁCDR=RC�Cang D'RD=ang D'RC=90���ł��邩��C
�@DR=DD'cos ang D'DC=DD'cos ang DCA�CRC=D'Ccos ang DCA=DD'cos ang DCA�C�����CD=2DD'cos ang DCA�D
�@���l��BE=2EE'cos ang ABE�D�j
�@���āCDD'=CD/(2cos ang
DCA),EE'=BE/(2cos ang ABE)�ł���̂ŁC
EE'>DD'�ł��邽�߂ɂ́Ccos ang
DCA>cos ang ABE���K�v�D
0<ang DCA,ang ABE<90�����C���炩��ang DCA<ang ABE�C�����D//
ang DCA,ang ABE<90�����Cang DCA>ang ABE�D
����CDD'��BC�̋�����d�CEE'��BC�̋�����e�Ƃ���ƁC���炩��d>e�C
D'����BC���������낵���̑���C�̋�����f�C
E'����BC���������낵���̑���B�̋�����g�Ƃ���ƁC
�O�����̒藝���CD'^2=DD'^2=d^2+f^2�CBE'^2=EE'^2=e^2+g^2�����C
DD'<EE'�Cd>e���Cg>f�C
�����ŁCang ABE,ang DCA<45���̂Ƃ��́Ce/g=tan
2ang ABE>d/f=tan 2ang DCA���ang ABE>ang DCA�C�����D
�����łȂ����́Cangle B,angle C�̂ǂ��炩���݊p�ƂȂ�D
ang B>90���̂Ƃ��CCD^2-d^2>BC^2>BE^2-e^2�ƂȂ薵���D
ang C>90���̂Ƃ��Cang ABE>ang DCA�����炩�ɂ킩��̂ŁC�����D
����āCDD'��EE'������ɂȂ��D
DD'�������ɗ��鎞�����l�D//
�m���U�u�O�p��K�v 11/01: 16��47�� ��M �X�V11/16
�@�@�@�@������@�@mizuryu@aqua.ocn.ne.jp
![]()
