平成１７年１月３日

[流れ星]

　　　　　第１４９回数学的な応募問題

　　　　　　＜解答募集期間：１月３日〜１月２３日＞
［外接する３円］

最近、中央新書から出版された秋山仁著の「知性の織りなす数学美」という本を読んでいます。その中に、
江戸時代の和算家『関孝和』のこぼれ話が出ていました。次の問題が出ていて、生徒と一緒に解き始めましたが、
未だに解けていません。では、その問題です。

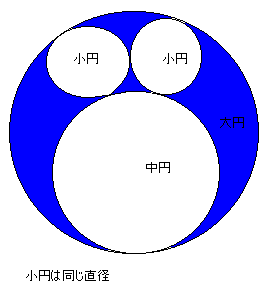
図の青の部分の面積が１２０、中円と小円の直径の差が５であるとき、大、中、小の３種類の直径を求めよ。
だだし、中円と小円は互いに外接、中円と大円は内接、２つの小円と大円は内接している。　

　　　【追記】１月３日の夜記入
実は、問題文は「知性の織りなす数学美」にある通りですが、生徒と考えていたとき気がついたのですが、図の青の部分の面積が１２０は誤記のような気がします。そこで、面積を１２０π（πは円周率）としても考えてください。

さらに、類題として、図の通りの４つの円で、大円、中円、小円の半径をそれぞれ、Ｒ，ｒ　，ｔ　としたとき、ｔをＲ，ｒで表してください。（この類題が和算の本にあるものです）
皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。
待っています。