kadai78

平成１７年１月２３日

[流れ星]

　　　　　第１４９回数学的な応募問題解答ＮＯ１

　　　　　　＜解答募集期間：１月３日～１月２３日＞
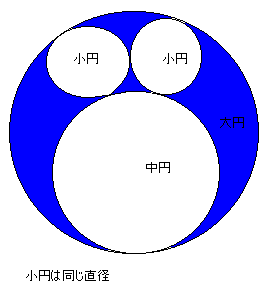
［外接する３円］

最近、中央新書から出版された秋山仁著の「知性の織りなす数学美」という本を読んでいます。その中に、
江戸時代の和算家『関孝和』のこぼれ話が出ていました。次の問題が出ていて、生徒と一緒に解き始めましたが、
未だに解けていません。では、その問題です。

図の青の部分の面積が１２０、中円と小円の直径の差が５であるとき、大、中、小の３種類の直径を求めよ。
だだし、中円と小円は互いに外接、中円と大円は内接、２つの小円と大円は内接している。　

　　　【追記】１月３日の夜記入
実は、問題文は「知性の織りなす数学美」にある通りですが、生徒と考えていたとき気がついたのですが、図の青の部分の面積が１２０は誤記のような気がします。そこで、面積を１２０π（πは円周率）としても考えてください。

さらに、類題として、図の通りの４つの円で、大円、中円、小円の半径をそれぞれ、Ｒ，ｒ　，ｔ　としたとき、ｔをＲ，ｒで表してください。（この類題が和算の本にあるものです）

ＮＯ１「H7K」　　 01/04: 23時21分受信更新1/23
あけましておめでとうございます，

ここの問題はいつも良い頭の体操になります．下手な数学の問題集をやるより効果があるかも……しれません．

計算用紙に図を書くだけでも一苦労．とりあえず，
類題として、「図の通りの４つの円で、大円、中円、小円の半径をそれぞれ、Ｒ，ｒ　，ｔ　としたとき、ｔをＲ，ｒで表してください。」
を考えてみました．
図の都合上，中円をR，小円をr，大円をtとしてしまいました．中円の中心に原点，2つの小円が接するところがy軸正の部分となるように座標軸をとる．
大円の中心をP(0,p), 片方の小円の中心を(r,n)とすると，
r^2 + n^2 = ( r + R )^2 ∴ n = sqrt( R^2 + 2rR ) ....<1>
t = p + R, ....<2>
( n - p )^2 + r^2 = ( t - r )^2 .... <3>
である．
<3>を展開：n^2 - 2np + p^2 = t^2 - 2rt
これに<1>, <2>を代入：R^2 + 2rR - 2np + p^2 = p^2 + R^2 + 2pR - 2rp - 2rR
∴ np = rp - pR + 2rR
∴ p ( n + R - r ) = 2rR
∴ p = 2rR / ( n + R - r ).
よって，
t = 2rR / ( n + R - r ) + R = 2rR / {sqrt( R^2 + 2rR ) + R - r} + R. ... ちょっと不自然だなあ．

これに，R - r = 5, t^2 - 2r^2 - R^2 = 120 という条件を入れれば，
出せると思うのですが……面倒そうだ．明日にまわします．

＜水の流れ：間違っていませんが・・・　綺麗な形でないですね。一考をお願いしたい。
これに，R - r = 5, 　実は和算家では半径を使わず、直径ばかりで考えていたと思われる＞

ＮＯ２「H7K」　　 01/05: 22時48分受信更新1/23
分母を有理化してみよう．
2rR / {sqrt( R^2 + 2rR ) + R - r}
= 2rR {sqrt( R^2 + 2rR ) - (R - r) } / {sqrt( R^2 + 2rR ) + R - r}{sqrt( R^2 + 2rR ) - (R - r)}
= 2R {sqrt( R^2 + 2rR ) - (R - r) } / {4R - r}
よって，
t = [ 2R {sqrt( R^2 + 2rR ) - (R - r) } + R ( 4R - r) ] / {4R - r}
= [ 2R sqrt( R^2 + 2rR ) + Rr + 2R^2 ] / {4R - r}
= R [ sqrt( R^2 + 2rR ) + r + 2R ] / {4R - r}
まだきれいじゃないなあ．

>> これに，R - r = 5, ＜実は和算家では半径を使わず、直経ばかりで考えていたと
>思われる＞
直径でしたか，見落としてました．

>ところが解けそうで解けていません私はね。
私も，「未知数4，式4本，解けそうだ……解けない，おかしいなあ」と感じました．
和算については，数値計算のほうに重点がおかれていたということを聞いたことがあります．
ひょっとしたら，数値計算じゃないと解けないのかもしれないな……などと思ってみたり．
% だったら，青の面積が120だというのもちょっとわかる気がするなあ．

＜水の流れ：数値を代入して近似値を出して行く方法で、和算家はこのように１桁づつ小さくして見つけていく話を聞いたことがあります。
　で、一筋縄ではいかないみたいです。＞

ＮＯ３「Toru」　 01/06: 16時38分受信更新1/23
あけましておめでとうございます。本年もよろしくお願いします。第１４９回の解答を送ります。新年から難問ですね。なかなか時間が取り難く、また前回同様少し根気がなくなっているようで、取りあえず送ってしまえという感じです。（もっとうまい方法もありそうだな、計算間違いもありそうだなetc,etc）大目に見て頂ければ幸いです。　
まずは類題から、
大円の中心をO、中円の中心をP、小円の中心を右からQ、Q’とする。OQ=OQ’=R-t,
よりΔOQ’Qは二等辺三角形でQ’Q の垂直２等分線はOを通り、PQ=PQ’=r+tだから,
これはPも通る。この直線をy軸としOを原点、x軸をy軸に直交するようにxy座標系を
考えると、O(0,0) ,P(0,r-R)となる。 Q(t,u) Q’(-t,u)とすると、
t^2+u^2=OQ^2=(R-t)^2 -----1)
t^2+(u+R-r)^2=PQ^2=(r+t)^2-------2)
1)よりt=(R^2-u^2)/2R---3) 　2)を整理して3)を代入すると、
(R+r)u^2+2R(R-r)u+R^2(R-3r)=0
((R+r)u+R(R-3r))(u+R)=0 よってu=R(3r-R)/(R+r)
3)へ代入してt=4Rr(R-r)/(R+r)^2 -----答え

次に本題を、
図の面積は120πとしました。
類題でt/r=a,(0<a<1) r/R=b (1/2<b<1)とすると
t=abR,r=bR,a=4(1-b)/(1+b)^2 -----3)
2(r-t)=5より2Rb(1-a)=5 両辺２乗して4R^2b^2(1-a)^2=25------4)
R^2-r^2-2t^2=120 よりR^2(1-b^2-2a^2b^2)=120 ------5)
3)を4),5)に代入してR^2を消去してひたすら計算すると
101b^6+1172b^5+3065b^4-3776b^3+999b^2-20b-5=0 左辺をF(b)とすると
F(1/2)<0, F(1)>0　-------6)
F’(b)=606b^5+5860b^4+12260b^3-11328b^2+1998b-20
F’’(b)=3030b^4+23440b^3+36780b^2-22656b+1998
F’’’(b)=12120b^3+70320b^2+73560b-22656
F’’’(1/2)>0より1/2<bでF’’’(b)>0, F’’(1/2)>0よりF’’(b)>0,F’(1/2)>0
よりF’(b)>0すなわちF(b)は1/2<b<1で単調増加、6)とあわせてこの範囲で唯一の解
を持つ。

Newton法を用いて近似解を計算する。b(n)=b(n-1)-F(b(n-1))/F’(b(n-1))
b(0)=1/2,としてエクセルで計算すると、b(6)以降0.54917078で一定となりました。
この時(r-5/2)/r=a よりr=5/2(1-a)と3)より
r=10.0564743, t=7.5564743, R=18.3121076
直径を求めているので２倍して、
大円36.6242151中円20.1129486小円15.1129486　------答え

ＮＯ４「H7K」　　 01/06: 21時41分受信更新1/23
設問要求は小円の半径を表せ，ということなので，そっちだったらきれいになるのかも．
前回のメールのあと，近似値を出してみました，その結果，
r=7.55647430068
R=10.05647430068
t=18.31210755413
ぐらいになりました．
P.S. 使ったプログラム(C++)はこんな感じ．組むのはそんなに時間かからない：

#include<iostream>
using namespace std;
int main(void){
double r,t,s; r=1; s=1;
for(;;){
cout.precision(16);
r=r+s;
cout << "r = " << r;
cout << "\nt = " << 2*r*(r+2.5)/(sqrt((r+2.5)*(r+2.5)+2*r*(r+2.5))+2.5)+(r+2.5);
t = 2.0*r*(r+2.5)/(sqrt((r+2.5)*(r+2.5)+2.0*r*(r+2.5))+2.5)+(r+2.5);
cout << "\n t^2 - 2r^2 - (r+2.5)^2 = " << t*t - 2.0*r*r - (r+2.5)*(r+2.5);
cout << "\n";
if ( t*t - 2.0*r*r - (r+2.5)*(r+2.5) > 120){r=r-s; s=s/10.0;}
}
}

ＮＯ５「Toru」　 01/07: 11時46分受信更新1/23
やはりいくつか訂正すべき点を思い付きましたので再送します。よろしくお願いします。

　1)中円ということで図からb>1/2と勝手に決めておりましたが、a=4(1-b)/(1+b)^2でa=1すなわちt=rとすればb=-3+2√3(=0.464--)となりますから-3+2√3<b<1の範囲で考えなければなりません。
　2)ニュートンの近似法を「解析概論」で見直すと、[a,b]でf(a)<0,f(b)>0
f''(x)>0ならb(1)=b-f(b)/f'(b),b(2)=b(1)-f(b(1))/f(b(1)),-----ととるとb>b(1)>b(2)>--->b(n)>----は[a,b]におけるf(x)=0の唯一の根に収束するということで、f''(x)>0なら充分,（実際区間[-3+2√3,1]ではF'(-3+2√3)<0となってしまって、F(b)は単調増加ではない）さらに起点は1の方に取った方がよかったようです。
（1/2からスタートしても区間内で収束したから答は一致していますが）
　というようなことでこの当たりを訂正して訂正版を送ります。よろしくお願いします。ついでに120πでなくて120の時も同様にやってみました。
計算はやや面倒になりますが、エクセルを使えばほぼ同じに答が出るようです。関孝和は円周率も１１桁まで求めていたというので、やはりこちらが本物でしょうか？　江戸時代にはエクセルはなかったでしょうからどうやったのか、機会があれば和算のことも勉強してみたいと思います（プログラムと同様思うだけかもしれませんが？！）　　
類題については前回解答参照して下さい。

120πの時、
類題でt/r=a,(0<a<1) r/R=bとすると
t=abR,r=bR,a=4(1-b)/(1+b)^2 -----3)
ここでa=1の時、b=-3+2√3 より-3+2√3 <b<1
2(r-t)=5より2Rb(1-a)=5 両辺２乗して4R^2b^2(1-a)^2=25------4)
R^2-r^2-2t^2=120 よりR^2(1-b^2-2a^2b^2)=120 ------5)
3)を4),5)に代入してR^2を消去してひたすら計算すると
101b^6+1172b^5+3065b^4-3776b^3+999b^2-20b-5=0
左辺をF(b)とすると、α=-3+2√3 としてエクセルを使って計算すると
F(α)<0, F(1)>0　-------6)
F’(b)=606b^5+5860b^4+12260b^3-11328b^2+1998b-20
F’’(b)=3030b^4+23440b^3+36780b^2-22656b+1998
F’’’(b)=12120b^3+70320b^2+73560b-22656
F’’’(α)>0より区間[α,1]でF’’’(b)>0, F’’(α)>0よりF’’(b)>0、よっ
てF(b)は下に凸で6)とあわせてα=-3+2√3<b<1で唯一の解を持つ。

Newton法を用いて近似解を計算してみるとb(n)=b(n-1)-F(b(n-1))/F’(b(n-1))
b(0)=1,としてエクセルで計算してみたら、b(8)以降0.54917078で一定となりました。
この時(r-5/2)/r=a と3)より
r=10.0564743, t=7.5564743, R=18.3121075
直径を求めているので２倍して、
大円36.6242151中円20.1129486小円15.1129486　------答え

原文のとおり１２０とすると
101b^6+1172b^5+3065b^4-3776b^3+999b^2-20b-5=0のところが
G(b)=(5+96/π)b^6+(20+1152/π)b^5+(185+2880/π)b^4-(320+3456/
π)b^3+(135+864/π)b^2-20b-5=0 π=3.1415926536
としてエクセルを利用して同様に計算すると、やはりG(1)>0, G(α)<0 同じようにG’
’’(α)>0,G’’(α)>0などから区間[α,1]で　G’’(b)>0 もえられてG(b)は下に
凸、G(b)=0はこの区間で唯一の解を持ち、b(0)=1からb(n)=b(n-1)-G(b(n-1))/G’
(b(n-1))を順に計算して行くとb(8)以降b=0.60959323　となりました。
この時r=6.2934384,t=3.7934384,R=10.3239965
直径ならば大円20.6479929,中円12.5868768,小円7.5868768

ＮＯ６「kasama」 01/07: 11時47分受信更新1/23
明けましておめでとうございます。本年もよろしくお願い致します。

今回の問題は一見簡単そうに思えたのですが、結構難しいですね。新年早々苦労しています。途中経過ですが、以下の通りご報告致します。

まず、類題から取り組みました。円の関係を一般化できると都合が良いと思ったからでして、・・・

　t=4*R*r*(R-r)/(R+r)^2
　ただし、大円の半径R、中円の中心r、小円の中心tを得ました。数式ソフトを利用したので難なくできました。この結果を利用する
と、本題が簡単に解けるだろうと思いきや、・・・やり方が悪いと言うか安易なやり方なので、6次方程式を解くハメになりました。5次以上の方程式は代数学的
に解けませんので、閃かない私の頭では・・・まぁ、数値計算なら代数法的式はたやすく解くことができまして、

　t=7.55647430067939
　r=10.05647430067939
　R=18.312107554126076

のようです。この値を目安にして何とか論理値を求めようと奮闘しています。では・・・

ＮＯ７「UnderBird]01/07: 17時15分受信更新1/23
中円の中心を原点(０，０)、半径ｒ＋５とすると
小円の中心は、（√(３ｒ^2＋２０ｒ＋２５)，±ｒ）、半径ｒ
また、大円の半径をＲとすると、πＲ^2＝２πｒ^2＋π（ｒ＋５）^2＋１２０π　よ
り
Ｒ＝√（３ｒ^2＋１０ｒ＋１４５）となるので、
大円の中心は、（－ｒ－５＋√（３ｒ^2＋１０ｒ＋１４５），０）となり、
大円の中心と２つの小円の中心を結ぶ二等辺三角形のｘ軸の上側の直角三角形から
三平方の定理を使うと、
式は出ますが、計算機を用いても厳密解は求まりませんでした。
ただし、近似値として、
ｒ≒６．４８４７６６９・・・というのはわかりました。

参考図です
http://homepage2.nifty.com/underbird/wasan.bmp
******************************

ＮＯ８「kasama」 01/08: 14時40分受信更新1/23
「toru」さんと同じ値ですから、論理値は無いのではそうなんですか。数値解析でしか解けないのですね。もう少し考えてみますが、やったところまでを文章化しましたので、添付ファイルにしてお送り致します。
類題】　3つの円の中心、半径を
　大･･･中心C_R(p,0),半径R　中･･･中心C_r(0,0), 半径r　小･･･中心C_t(√{(r+t)²-t²}, t),半径t
とします（下図参照）。

すると、
　R = p+r
　R = |C_t-C_R|+t ⇒ (R-t)² = t²+(√{(r+t)²-t²}-p)²
なので、この２式からpを消去すると、
　4t(r²t+2Rr(2r+t)-R²(4r-t)) = 0 ⇒ r²t+2Rr(2r+t)-R²(4r-t) = 0 (∵T>0)
となり、tについて整理すると、
　t = 4Rr(R-r)/(R+r)² ･･･(1)
です。

【本題】
解決できていませんが、できたところまでを記載します。まず、『青の部分の面積が120π』より
　πR²-(πr²+2πt²) = 120π ⇒ R²-r²-2t² = 120 ･･･(2)
また、『中円と小円の直径の差が5』より
　r=t+5/2 ･･･(3)
です。(1)、(2)、(3)式からR、rを消去してtについて整理すると、
　44t⁶+440t⁵+460t⁴-7750t³-154600t²-905875t-1515000 = 0
となりますが、現時点で、この方程式を解析的に解くことができていません。が、数値計算で解くことは容易でして、重解、複素数も含めて、以下の解がありました。
　t=-8.922821863142532, -3.7990431791452033, -3.1676141827927538(重解)
　 -0.833497537799448+j6.460730985978614, 7.55647430067939
このうち条件を満たすのは、t=7.55647430067939ですから、3つの円の半径は
　t=7.55647430067939、r=10.05647430067939、R=18.312107554126076　です。

ＮＯ９「三角定規」01/08: 22時39分受信更新1/23
問題149の解答を送ります。