平成１７年４月１７日

[流れ星]

　　　　　第１５３回数学的な応募問題解答

　　　　　　＜解答募集期間：３月２７日〜４月17日

［和算家の問題］

先日、「第８回和算に学ぶ」会に出席したところ、次の問題が紹介されました。

図のような長方形ＡＢＣＤの周および内部の点Ｐから各頂点に至る長さをＢＰ＝１５，ＣＰ＝２４，ＤＰ＝２０
とするとき、次の問に答えよ。

問題１：ＡＰの長さを求めよ。

問題２：長方形の面積の最大値を求めよ。また、そのときの２辺の長さも求めよ。

問題３：長方形の面積の最小値を求めよ。また、そのときの２辺の長さも求めよ。

ＮＯ１「H7K」　　 3/27: 21時58分受信 更新4/17

% 途中までです．数値計算がまだです．
% 平方根はsqrt()で表しています．
PからAB, BCへ垂線を下ろし，それぞれ足をH,Iとする．
AH=r, HB=p, BI=q, IC=sとする．
(1)
与えられた条件と三平方の定理より，
p^2+q^2=225,
p^2+s^2=576,
s^2+r^2=400
が得られる．(この3式をまとめて(a)とする．)
これを加減して
q^2+r^2=49
を得るが，これはAP^2=49，すなわちAP=7であることを示している．

(2), (3)
qを固定する．□ABCDの面積をTとおく．
すると，
p=sqrt(225-q^2), r=sqrt(49-q^2), s=sqrt(351+q^2),
T=(q+s)(p+r)
である．Tをqで微分，整理すると，計算の末
dT/dq=(1+q/s)(1/p+1/r)(pr-qs)
となる．qのとりうる範囲は当然0<=q<=7であることを考えると，
dT/dqの前2項は導関数を考えればよい範囲0<q<7では常に正の値である．
また，w(q):=pr-qsとすると，w(0)=105>0, w(7)=-140<0で，かつ
p, rは0<q<7で単調増加，q, sは単調減少だから，
w(n)=0を満たす0<n<7が唯一存在する．
よって，Tの値は，0<q<nでは増加，n<q<7で減少．

さて，nの値を求める．
pr-qs=o iff p:q=s:rより，
p=na, q=ma, r=mb, s=nbとおけ，また
q^s+r^2:s^2+p^2=m^2:n^2=49:576より，m:n=7:24．
よって，
p=24a, q=7a, r=7b, s=24bとおける．
すると，(a)に代入して
576a^2+576b^2=576,
625b^2=400
が得られる．a,b>0だから，b=0.8, a=0.6．
よって，n=4.2．

＜水の流れ：和算家は微分することを知っていましたし、その値が０となるときに
最大値か最小値になることも経験から知っていましたという話で終わっていました。言葉は「適尺法級法」と言いますけど。＞
そうだったんですか．「和算」と聞いたので，微積は使わなくても解けるのではと，しばらく悩んだんですが，これでも十分正統なんですね．

さて，計算の結果，(前回の記法に倣うと)
q=0のとき，T=22sqrt(351)=66sqrt(39)=412.169.
q=7のとき，T=27sqrt(176)=108sqrt(11)=358.196.
q=4.2のとき，T=...=468.
従って，

最大はq=4.2のときに達成され，そのときの四角形の面積は468，
2辺の長さはそれぞれ20, 23.4．
( (p,q,r,s)=(5.6,4.2,14.4,19.2) )

最小はq=7のときに達成され，そのときの四角形の面積は108sqrt(11)，
2辺の長さはそれぞれ4sqrt(11), 27．
( (p,q,r,s)=(0,7,4sqrt(11),20) )

ＮＯ２「kashiwagi」3/29: 20時01分受信 更新4/17
お世話になります。今回の和算の問題面白く考えさせて頂きました。
極端な場合を 考えれば良いと思いますが、兎も角数値があまりにも汚いので自身がもてません。

153回解答

問１．

　長方形ABCDの点Aを原点に置き、辺ADをｘ軸上に辺ABをｙ軸上におき、ADの長さをa、ABの長さをｂとする。又、点Pの座標を（ｘ、ｙ）とし、APの長さをLとする。すると三平方の定理より、

ｘ^２＋ｙ^２＝L^２　　　　・・・・・�@

（x-a）^２＋ｙ^２＝２０^２　　　・・・・・�A

（x-a）^２＋（ｙ-ｂ）^２＝２４^２　・・・・・�B

ｘ^２＋（ｙ-ｂ）^２＝１５^２　　　　・・・・・�C　　　　が成立する。

ここで�A＋�C−�Bを計算すると、ｘ^２＋ｙ^２＝２０^２＋１５^２−２４^２＝７^２となる。因って�@より求める値、APの長さは７となる。

問2．＆問３．

長方形の中の点Pが動ける範囲は点Aを中心とする４分の1円である。即ちｙ軸上からｘ軸上まで移動する。
因って点Pがｙ軸上にきた時ABの長さは２２、三角形ADPに三平方の定理を適用し、ADの長さを求めると２０^２−７^２＝３５１より３√３９となる。
因って長方形の面積は６６√３９となる。

これと全く同様の計算で点Pがｘ軸上にきた時ADの長さは２７、三角形ABPに三平方の定理を適用し、ABの長さを求めると１５^２−７^２＝１７６より４√１１となる。
因って長方形の面積は１０８√１１となる。

更に点Pが対角線AC上にある場合をかんがえる。今∠CADをθとして４個の三角形各々に余弦第２定理を適用し、aとｂを求めると、夫々√（１０８８１/１７）と√（５４５６/１７）となる。因って長方形ABCDの面積は３７２√４２９/１７となる。

以上の計算より、

最大面積は３７２√４２９/１７、２辺の長さは４√（３４１/１７）と３√（１２０９/１７）となる。

最小面積は１０８√１１、２辺の長さは２７と４√１１となる。

ＮＯ３「Toru」 3/30: 16時07分受信 更新4/17
第１５３回の解答を送ります。どうも腕力のみで今一つの解答ですが、他のよい方法
も思い付かず、といったところです。　

問題１
PからBCと平行な直線を引きAB,DCとの交点をQ、S
PからCDと平行な直線を引きAD,BCとの交点をT、Rとする

BQ^2+BR^2=BP^2=15^2 -------1)
CR^2+CS^2=CP^2=24^2 -------2)
DS^2+DT^2=DP^2=20^2 -------3)
1)+3)-2) とすると DT=CR,BQ=CS
より
BR^2+DS^2=AQ^2+AT^2= AP^2=15^2+20^2-24^2=49
よってAP=7

問題２、３
AB=DC=2xとおく
ABはAPDが一直線上にある時最小になりこの時
AB=√(15^2-7^2)=√176
ABはAPBが一直線上にある時最大でこの時
AB=22
よって√176/2≦x≦11、 x^2=tとして　44≦t≦121
ΔAPBにヘロンの公式をつかうとs=(7+15+2x)/2=11+xより
ΔAPB=√(11+x)(11-x)(4+x)(-4+x) =√(11^2-x^2)(x^2-4^2)=√(121-t)(t-16)
同様に
ΔDPC=√(22+x)(22-x)(2+x)(-2+x)=√(484-t)(t-4)

長方形ABCDの面積をSとして
S/2=ΔAPB+ΔDPC=√(121-t)(t-16)+√(484-t)(t-4)=F(t)とする
F’(t)=(-2t+137)／ 2√(121-t)(t-16)+(-t+244)／√(484-t)(t-4)
F’(t)=0として(-2t+137)／ 2√(121-t)(t-16)=(t-244)／√(484-t)(t-4)
両辺を二乗してひたすら計算すると、
t^4とt^3の項は消えて、
219375 t^2-26184600 t+424710000=0
これは8775 で割れて
25t^2-2984 t+48400=(25t-484)(t-100)=0 より　t=484/25,100 このうちt=100がF’
(t)=0を満たす。
F’(t)は 44≦t＜121で連続
F’(44)>0  t=121の近くでF’(t)<0 だから　F(t)はt=100で極大値かつ最大値を取る。
この時、長方形の面積は2F(100)=468 でAB=20 BC=23.4

最小値はF(44)or F(121)であるが、
F(44)=54√11＜F(121)=33√39　より
よりt=44の時最小で、この時長方形の面積は108√11でAB=4√11  BC=27

ＮＯ４「kasama」 3/31: 17時21分受信 更新4/17
【問題１】

�@座標の割当て
以下の通り各点に座標を割り当てます。
　P=(0,0)、A=(X_a,Y_a)、B =(X_a,Y_c)、C=(X_c,Y_c)、 D=(X_c, Y_a)　ただし、X_a<X_c、 Y_a>Y_c

�A条件を適用
線分の長さが、PB=15、PC=24、PD=20なので、三平方の定理により
　X_a²+Y_c²=15² ･･･(1)
　X_c²+Y_c²=24² ･･･(2)
　X_c²+Y_a²=20² ･･･(3)
ですが、(1)-(2)+(3)とやって整理すると、
　X_a²+Y_a²=49 ⇒ AP=7
です。


【問題２、３】

長方形の面積Sは
　S=(X_c-X_a)(Y_a-Y_c) ･･･(4)
と表現できまして、条件(1)〜(3)式のもとで最小値･最大値を求めれば良いのすが、単純にやると数式が複雑で大変そうなので、少し工夫が必要ですね。長方形は下図のように点A_1〜2間で連続的に変化していると思われます。

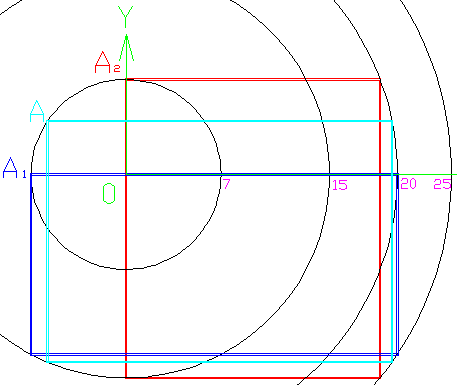
なので、直感的にSの最小値･最大値を求めるには、点A₁、A₂の値または点A_1〜2間の極値を調べれば良いことがわかります。

�@点A_1〜2間の極値
ある条件下での極値さえわかれば良いので、Lagrangeの乗数法を用いるのが簡単かと思います。(1)〜(3)式を
　g₁=X_a²+Y_c²-225
　g₂=X_c²+Y_c²-576
　g₃=X_c²+Y_a²-400
として、未定乗数をλ_1〜3として、次の関数Fを導入します。
　F=S+Σg_i (i=1,2,3)
で、FをX_a,Y_a,X_c,Y_c,λ_1〜3 で微分して、0とやると
　Y_a-Y_c-2X_aλ₁=0 ･･･(5)
　X_a-X_c-2Y_aλ₃=0 ･･･(6)
　Y_a-Y_c+2X_cλ₂+2X_cλ₃=0 ･･･(7)
　X_a-X_c+2Y_cλ₁+2Y_cλ₂=0 ･･･(8)
　X_a²+Y_c²-225=0 ･･･(9)
　X_c²+Y_c²-576=0 ･･･(10)
　X_c²+Y_a²-400=0 ･･･(11)
となります。(5)〜(7)をλ_1〜3について解くと
　λ₁=(Y_a-Y_c)/(2X_a)
　λ₂=(X_c²-Y_a²-X_aX_c+Y_aY_c)/(2X_cY_a)
　λ₃=(X_a-X_c)/(2Y_a)
(8)式に代入して、整理すると
　(X_a-X_c)(Y_a-Y_c)(X_aX_c-Y_aY_c)=0
ですが、X_a<X_c、Y_a>Y_cなので、
　X_aX_c=Y_aY_c ⇒ Y_c=X_aX_c/Y_a ･･･(12)
(12)式を(9)、(10)式に適用して整理すると、
　X_a²X_c²+X_a²Y_a²-225Y_a²=0 ･･･(13)
　X_a²X_c²+X_c²Y_a²-576Y_a²=0 ･･･(14)
です。ここまで整理すると、(11)〜(14)式の有効解は簡単に求まりして、
　X_a=-21/5、Y_a=28/5、X_c=96/5、 Y_c=-72/5
です。(4)式に代入して、極値が求まります。
　S=468、AB=117/5、BC=20

�A点A₁、A₂の面積
点A₁では、X_a=-7、Y_a=0、 X_c=20、 Y_c=-4√11なので、
　S=108√11≒358.2、AB=27、BC=4√11
点A₂では、X_a=0、Y_a=7、 X_c=3√39、 Y_c=-15なので、
　S=66√39≒412.2、AB=3√39、BC=22

�B最小値･最大値
�@�Aより、
　2辺の長=27、4√11のとき最小値=108√11
　2辺の長=117/5、20のとき最大値=468
です。

ＮＯ５「cbc&anniss」4/01: 00時45分受信 更新4/17

ＮＯ６「ice」 　4/09: 17時29分受信 更新4/17
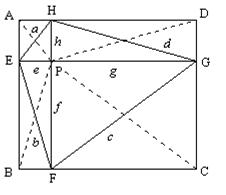
こんにちは。（ペンネーム「ice」でお願いします。）
第153回応募問題の解答を考えましたので、お送りします。今回も楽しませていただきました。今後ともよろしくお願いします。

ＮＯ7「中川幸一」4/19: 05時25分受信 更新4/24

「解答」です。