平成１７年４月１７日

[流れ星]

　　　　　第１５４回数学的な応募問題

　　　　　　＜解答募集期間：４月１７日〜５月１７日

［ピックの公式］

皆さん、多角形の面積を求める素晴らしい公式を紹介します。ここでは、手順にしたがって、証明していきます。

公式：すべての頂点が格子点にある多角形が、内部にａ個の格子点をもち、周上にｂ個の格子点をもつとき、その面積は
　　　格子の間隔を１とすると、　a＋（ｂ／２）−１　である。

手順１：格子の線上に４辺がある長方形のとき、ピックの公式を証明せよ。

手順２：格子の線上に直角をはさむ２辺がある直角三角形のとき、ピックの公式を証明せよ。

手順３：多角形Ａが２つの多角形Ｂ，Ｃに分割されるとき（その１）
　　　　　多角形Ｂ，Ｃに対してピックの公式が成り立つならばＡに対しても成り立つことを証明せよ。

手順４：多角形Ａが２つの多角形Ｂ，Ｃに分割されるとき（その１）
　　　　　多角形Ａ，Ｂに対してピックの公式が成り立つならばＣに対しても成り立つことを証明せよ。

手順５：格子点上に頂点をもつ一般の三角形のとき、三角形の頂点を通り、４辺が格子線上にある図のような長方形を考える。
　　　　　この図を利用して、ピックの公式を証明せよ。（文章表現になる）

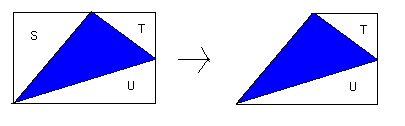
点順６：格子点を結んでできる一般の多角形のとき、ピックの公式を証明せよ。（文章表現になる）

＜問題の出典：中高一貫数学コース「数学�Tをたのしむ」志賀浩二著　岩波書店＞

皆さん、答えがわかったら、一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。
待っています。